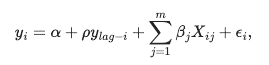Spatial Lag Model

The presence of spatial dependence indicates that values of observations are related to each other through distance, and the spatial lag model that includes this dependence is expected to perform better. The spatial lag model is also known as Spatial Autoregressive Model (SAR).

The SAR model considers spatial dependence over the target variable, meaning that the value of a region's target variable is related to its neighbors' target variable.

The SAR model includes the spatial lag of the dependent variable into the linear equation. This results in an extra parameter associated with the spatial lag of the dependent variable as shown in the following formula.

Description of the illustration sar_formula.png

The equation can be represented as shown:

Description of the illustration sar_equation.png

In the preceding equation, W is the standardized spatial weights matrix, and ρ is called the spatial autoregressive coefficient.

The SpatialLagRegressor class requires setting of the spatial_weights_definition parameter, which establishes the relationship between neighboring observations. The following table describes the main methods of the SpatialLagRegressor class.

Method	Description
fit	Trains the SpatialLagRegressor model from the given training data. The model includes a parameter for the spatial lag of the target variable.
predict	Uses the trained parameters, including the one associated with the spatial lag of the target variable, to estimate the target variable of the given data.
fit_predict	Calls the fit and predict methods sequentially with the training data.
score	Returns the R-squared statistic for the given data.

See the SpatialLagRegressor class in Python API Reference for Oracle Spatial AI for more information.

The following example uses the block_groups SpatialDataFrame. It creates an instance of the SpatialLagRegressor class defining the spatial_weights_definition parameter. Then, it creates a spatial pipeline with a preprocessing step to standardize the data and applies the Spatial Lag model at the final step.

The model is trained using a training set (X_train) and the MEDIAN_INCOME column as the target variable. Finally, it calls the predict and score methods with a test set (X_test) to estimate the values of the target variables and obtain the model's R-Square score respectively.

from oraclesai.preprocessing import spatial_train_test_split 
from oraclesai.weights import KNNWeightsDefinition 
from oraclesai.regression import SpatialLagRegressor 
from oraclesai.pipeline import SpatialPipeline 
from sklearn.preprocessing import StandardScaler 

# Define features
X = block_groups[["MEDIAN_INCOME", "MEAN_AGE", "HOUSE_VALUE", "INTERNET", "geometry"]] 

# Define training and test sets
X_train, X_test, _, _, _, _ = spatial_train_test_split(X, y="MEDIAN_INCOME", test_size=0.2, random_state=32) 

# Create an instance of SpatialLagRegressor
spatial_lag_model = SpatialLagRegressor(spatial_weights_definition=KNNWeightsDefinition(k=5)) 

# Add the model in a Spatial Pipeline with a preprocessing step
spatial_lag_pipeline = SpatialPipeline([("scaler", StandardScaler()), ("spatial_lag", spatial_lag_model)]) 

# Train the model with MEDIAN_INCOME as the target variable
spatial_lag_pipeline.fit(X_train, "MEDIAN_INCOME") 

# Print the predictions with the test set
spatial_lag_predictions_test = spatial_lag_pipeline.predict(X_test.drop(["MEDIAN_INCOME"])).flatten() 
print(f"\n>> predictions (X_test):\n {spatial_lag_predictions_test[:10]}") 

# Print the R-squared metric with the test set
spatial_lag_r2_score = spatial_lag_pipeline.score(X_test, y="MEDIAN_INCOME") 
print(f"\n>> r2_score (X_test):\n {spatial_lag_r2_score}")

The program produces the following output:

>> predictions (X_test):
 [ 92285.13545208 100551.0381313   30910.61123168  45166.3218764
 177515.68764358  44088.89962954  98205.35728383  27788.19879028
  72553.17695035  24875.81828048]

>> r2_score (X_test):
 0.6150829472253789