3 Regression
Learn how to predict a continuous numerical target through regression - the supervised machine learning technique.
3.1 About Regression
Regression is a machine learning technique that predicts numeric values along a continuum.
Profit, sales, mortgage rates, house values, square footage, temperature, or distance can be predicted using Regression techniques. For example, a regression model can be used to predict the value of a house based on location, number of rooms, lot size, and other factors.
A regression task begins with a data set in which the target values are known. For example, a regression model that predicts house values can be developed based on observed data for many houses over a period of time. In addition to the value, the data can track the age of the house, square footage, number of rooms, taxes, school district, proximity to shopping centers, and so on. House value can be the target, the other attributes are the predictors, and the data for each house constitutes a case.
In the model build (training) process, a regression algorithm estimates the value of the target as a function of the predictors for each case in the build data. These relationships between predictors and target are summarized in a model, which can then be applied to a different data set in which the target values are unknown.
Regression models are tested by computing various statistics that measure the difference between the predicted values and the expected values. The historical data for a regression project is typically divided into two data sets: one for building the model, the other for testing the model.
Regression modeling has many applications in trend analysis, business planning, marketing, financial forecasting, time series prediction, biomedical and drug response modeling, and environmental modeling.
3.1.1 How Does Regression Work?
Estimate target values as a function of predictors, minimizing error to fit a set of data observations.
You do not need to understand the mathematics used in regression analysis to develop and use quality regression models for machine learning. However, it is helpful to understand a few basic concepts.
Regression analysis seeks to determine the values of parameters for a function that cause the function to best fit a set of data observations that you provide. The following equation expresses these relationships in symbols. It shows that regression is the process of estimating the value of a continuous target (y) as a function (F) of one or more predictors (x1 , x2 , ..., xn), a set of parameters (θ1 , θ2 , ..., θn), and a measure of error (e).
y = F(x,θ) + e
The predictors can be understood as independent variables and the target as a dependent variable. The error, also called the residual, is the difference between the expected and predicted value of the dependent variable. The regression parameters are also known as regression coefficients.
The process of training a regression model involves finding the parameter values that minimize a measure of the error, for example, the sum of squared errors.
There are different families of regression functions and different ways of measuring the error.
3.1.1.1 Linear Regression
Use linear regression to model relationships with a straight line, predicting outcomes based on one or more predictors.
A linear regression technique can be used if the relationship between the predictors and the target can be approximated with a straight line.
Regression with a single predictor is the easiest to visualize. Simple linear regression with a single predictor is shown in the following figure:
Figure 3-1 Linear Regression With a Single Predictor
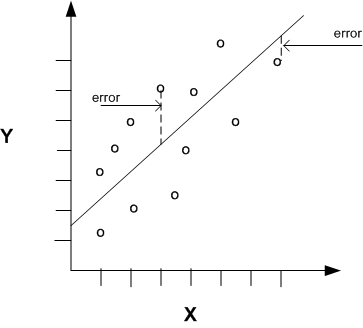
Description of "Figure 3-1 Linear Regression With a Single Predictor"
Linear regression with a single predictor can be expressed with the following equation.
y = θ2x + θ1 + e
The regression parameters in simple linear regression are:
-
The slope of the line (2) — the angle between a data point and the regression line
-
The y intercept (1) — the point where x crosses the y axis (x = 0)
3.1.1.2 Multivariate Linear Regression
Apply linear regression with multiple predictors, expanding the equation to include all relevant parameters.
The term multivariate linear regression refers to linear regression with two or more predictors (x1, x2, …, xn). When multiple predictors are used, the regression line cannot be visualized in two-dimensional space. However, the line can be computed by expanding the equation for single-predictor linear regression to include the parameters for each of the predictors.
y = θ1 + θ2x1 + θ3x2 + ..... θn xn-1 + e
3.1.1.3 Regression Coefficients
Evaluate the impact of predictors using regression coefficients in multivariate linear regression.
In multivariate linear regression, the regression parameters are often referred to as coefficients. When you build a multivariate linear regression model, the algorithm computes a coefficient for each of the predictors used by the model. The coefficient is a measure of the impact of the predictor x on the target y. Numerous statistics are available for analyzing the regression coefficients to evaluate how well the regression line fits the data.
3.1.1.4 Nonlinear Regression
Represent complex relationships between predictors and targets using nonlinear regression techniques.
Often the relationship between x and y cannot be approximated with a straight line. In this case, a nonlinear regression technique can be used. Alternatively, the data can be preprocessed to make the relationship linear.
Nonlinear regression models define y as a function of x using an equation that is more complicated than the linear regression equation. In the following figure, x and y have a nonlinear relationship.
Figure 3-2 Nonlinear Regression With a Single Predictor
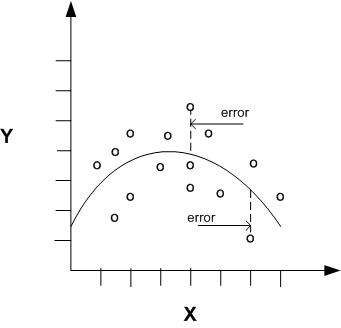
Description of "Figure 3-2 Nonlinear Regression With a Single Predictor"
3.1.1.5 Multivariate Nonlinear Regression
Perform nonlinear regression with multiple predictors to capture data relationships.
The term multivariate nonlinear regression refers to nonlinear regression with two or more predictors (x1, x2, …, xn). When multiple predictors are used, the nonlinear relationship cannot be visualized in two-dimensional space.
3.1.1.6 Confidence Bounds
Identify the range in which predicted values are likely to lie, enhancing prediction reliability.
A regression model predicts a numeric target value for each case in the scoring data. In addition to the predictions, some regression algorithms can identify confidence bounds, which are the upper and lower boundaries of an interval in which the predicted value is likely to lie.
When a model is built to make predictions with a given confidence, the confidence interval is produced along with the predictions. For example, a model predicts the value of a house to be $500,000 with a 95% confidence that the value is between $475,000 and $525,000.
3.2 Testing a Regression Model
Apply a regression model to test data, compare predicted values with actual ones, and use metrics to evaluate accuracy.
A regression model is tested by applying it to test data with known target values and comparing the predicted values with the known values.
The test data must be compatible with the data used to build the model and must be prepared in the same way that the build data was prepared. Typically the build data and test data come from the same historical data set. A percentage of the records is used to build the model; the remaining records are used to test the model.
Test metrics are used to assess how accurately the model predicts these known values. If the model performs well and meets the business requirements, it can then be applied to new data to predict the future.
3.2.1 Regression Statistics
Use Root Mean Squared Error (RMSE) and Mean Absolute Error (MAE) to assess the quality of regression models.
The Root Mean Squared Error and the Mean Absolute Error are commonly used statistics for evaluating the overall quality of a regression model. Different statistics may also be available depending on the regression methods used by the algorithm.
3.2.1.1 Root Mean Squared Error
Calculate the Root Mean Squared Error (RMSE) to determine the average squared distance of data points from the fitted line.
The following SQL expression calculates the RMSE:
SQRT(AVG((predicted_value-actual_value) * (predicted_value-actual_value)))
This formula shows the RMSE in mathematical symbols. The large sigma character represents summation; j represents the current predictor, and n represents the number of predictors.
3.2.1.2 Mean Absolute Error
Compute the Mean Absolute Error (MAE) to find the average of the absolute residuals (errors), indicating prediction accuracy.
The MAE is very similar to the RMSE but is less sensitive to large errors.
This SQL expression calculates the MAE.
AVG(ABS(predicted_value-actual_value))
This formula shows the MAE in mathematical symbols. The large sigma character represents summation; j represents the current predictor, and n represents the number of predictors.
3.3 Regression Algorithms
Oracle Machine Learning supports these algorithms for regression: Generalized Linear Model (GLM), Neural Network (NN), Support Vector Machines (SVM), and XGBoost.
GLM and SVM algorithms are particularly suited for analysing data sets that have very high dimensionality (many attributes), including transactional and unstructured data.
-
GLM is a popular statistical technique for linear modeling. Oracle Machine Learning for SQL implements GLM for regression and for binary classification. GLM provides extensive coefficient statistics and model statistics, as well as row diagnostics. GLM also supports confidence bounds.
-
Neural Network is a powerful algorithm that can learn arbitrary nonlinear regression functions.
-
SVM is a powerful, state-of-the-art algorithm for linear and nonlinear regression. OML4SQL implements SVM for regression, classification, and anomaly detection. SVM regression supports two kernels: the Gaussian kernel for nonlinear regression and the linear kernel for linear regression.
-
XGBoost is machine learning algorithm for regression and classification that makes available the XGBoost open source package. Oracle Machine Learning for SQL XGBoost prepares training data, invokes XGBoost, builds and persists a model, and applies the model for prediction.

