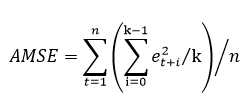14 Time Series
Learn about time series as an Oracle Machine Learning regression function.
- About Time Series
Time series is a machine learning technique that forecasts target value based solely on a known history of target values. It is a specialized form of regression, known in the literature as auto-regressive modeling. - Choosing a Time Series Model
Selecting a model depends on recognizing the patterns in the time series data. Consider trend, seasonality, or both that affect the data. - Automated Time Series Model Search
Automatically determine the best model type for time series forecasting if no specific model is defined. - Multiple Time Series Models
Multiple time series is a convenience operation for constructing multiple time series models with a common time interval for use as input to a time series regression. - Time Series Regression
Enhance time series regression with multi-series build by including additional features or related series to improve accuracy. - Time Series Statistics
Learn to evaluate model quality by applying commonly used statistics. - Time Series Algorithm
Oracle Machine Learning uses Exponential Smoothing to forecast from time series data.
Related Topics
Parent topic: Machine Learning Techniques
14.1 About Time Series
Time series is a machine learning technique that forecasts target value based solely on a known history of target values. It is a specialized form of regression, known in the literature as auto-regressive modeling.
The input to time series analysis is a sequence of target values. A case id column specifies the order of the sequence. The case id can be of type NUMBER or a date type (date, datetime, timestamp with timezone, or timestamp with local timezone). Regardless of case id type, the user can request that the model include trend, seasonal effects or both in its forecast computation. When the case id is a date type, the user must specify a time interval (for example, month) over which the target values are to be aggregated, along with an aggregation procedure (for example, sum). Aggregation is performed by the algorithm prior to constructing the model.
The time series model provide estimates of the target value for each step of a time window that can include up to 30 steps beyond the historical data. Like other regression models, time series models compute various statistics that measure the goodness of fit to historical data.
-
Projecting return on investment, including growth and the strategic effect of innovations
-
Addressing tactical issues such as projecting costs, inventory requirements and customer satisfaction
-
Setting operational targets and predicting quality and conformance with standards
Related Topics
Parent topic: Time Series
14.2 Choosing a Time Series Model
Selecting a model depends on recognizing the patterns in the time series data. Consider trend, seasonality, or both that affect the data.
Time series data may contain patterns that can affect predictive accuracy. For example, during a period of economic growth, there may be an upward trend in sales. Sales may increase in specific seasons (bathing suits in summer). To accommodate such series, it can be useful to choose a model that incorporates trend, seasonal effects, or both.
Trend can be difficult to estimate, when you must represent trend by a single constant. For example, if there is a grow rate of 10%, then after 7 steps, the value doubles. Local growth rates, appropriate to a few time steps can easily approach such levels, but thereafter drop. Damped trend models can more accurately represent such data, by reducing cumulative trend effects. Damped trend models can better represent variability in trend effects over the historical data. Damped trend models are a good choice when the data have significant, but variable trend.
Note:
Multiplicative error is not an appropriate choice for data that contain zeros or negative values. Thus, when the data contains such values, it is best not to choose a model with multiplicative effects or to set error type to be multiplicative.Parent topic: Time Series
14.3 Automated Time Series Model Search
Automatically determine the best model type for time series forecasting if no specific model is defined.
If you do not specify a model type (EXSM_MODEL) the default
behavior is for the algorithm to automatically determine the model type. The ESM
settings are listed in DBMS_DATA_MINING — Algorithm Settings:
Exponential Smoothing. Time
Series model search considers a variety of models and selects the best
one. For seasonal models, the seasonality is
automatically determined.
EXSM_MODEL setting is not defined thereby allowing the
algorithm to select the best model.
BEGIN DBMS_DATA_MINING.DROP_MODEL('ESM_SALES_FORECAST_1');
EXCEPTION WHEN OTHERS THEN NULL; END;
/
DECLARE
v_setlst DBMS_DATA_MINING.SETTING_LIST;
BEGIN
v_setlst('ALGO_NAME') := 'ALGO_EXPONENTIAL_SMOOTHING';
v_setlst('EXSM_INTERVAL') := 'EXSM_INTERVAL_QTR';
v_setlst('EXSM_PREDICTION_STEP') := '4';
DBMS_DATA_MINING.CREATE_MODEL2(
MODEL_NAME => 'ESM_SALES_FORECAST_1',
MINING_FUNCTION => 'TIME_SERIES',
DATA_QUERY => 'select * from ESM_SH_DATA',
SET_LIST => v_setlst,
CASE_ID_COLUMN_NAME => 'TIME_ID',
TARGET_COLUMN_NAME => 'AMOUNT_SOLD');
END;
/Parent topic: Time Series
14.4 Multiple Time Series Models
Multiple time series is a convenience operation for constructing multiple time series models with a common time interval for use as input to a time series regression.
One of the time series models is identified as the target time series of interest. All of the time series output is produced for the target. The other time series are assumed to be correlated with the target. This operation produces backcasts and forecasts on each time series and computes upper and lower confidence bounds for the identified target series. This operation can be used to forecast a wide variety of events, such as rainfall, sales, and customer satisfaction.
In the example of weather forecasting, the temperature and humidity attributes can be considered as the dependent or correlated time series and rainfall can be identified as the target time series.
- Backcasts in Time Series
In the rainfall, temperature, and humidity multiple time series example, backcasts are the estimate produced by the model for historical data. - How to Build Multiple Time Series Models
Oracle's exponential smoothing is enhanced to handle the building of multiple time series models with a single call to the model build method, in addition to single time series forecasting.
Related Topics
Parent topic: Time Series
14.4.1 Backcasts in Time Series
In the rainfall, temperature, and humidity multiple time series example, backcasts are the estimate produced by the model for historical data.
For example, if rainfall is dependent on humidity, then it is useful to have a value of humidity for the period of interest. For periods that have already occurred and are being used to construct the model, such as last week, it is necessary to have the humidity from last week and not from last month.
Parent topic: Multiple Time Series Models
14.4.2 How to Build Multiple Time Series Models
Oracle's exponential smoothing is enhanced to handle the building of multiple time series models with a single call to the model build method, in addition to single time series forecasting.
Multiple time series is built by specifying a series list
EXSM_SERIES_LIST. The rest of the parameters are the same as in
ESM model. In the weather forecast example, you can have a build data set and a
score data set. The build data set contains the identified target series (rain), the
dependent series: temperature and humidity. The DM$VP model detail
view is used to display a forecast for the identified target series (rain), along
with dependent series: temperate, and humidity. The DM$VR model
detail view is used to display backcasts for target series (rain), humidity, and
temperature. The backcasts and forecasts of the time series model can be fed into a
regression technique like generalized linear model, neural network, or XGBoost for time series regression.
In the
following example, the target attribute DAX is a Stock market index that is being
forecast. The dependent attributes that are also popular stock market indexes - SMI,
CAC, FTSE are passed as multiple series attributes. Exponential Smoothing settings
are used to build a multiple time series model by specifying a series list
(EXSM_SERIES_LIST) with multiple attributes.
Parent topic: Multiple Time Series Models
14.5 Time Series Regression
Enhance time series regression with multi-series build by including additional features or related series to improve accuracy.
Time series regression is possible with the multi-series build. Time series regression expands the features that can be included in a time series model and possibly improves forecast accuracy. Some of the additional features can be other time series that are thought to be related or dependent to the "target" series. Temperature and humidity are both dependent time series with rainfall, so by looking at historical data for these two attributes, we can make predictions about future rainfall. When the temperature is high and the humidity is high, there is a greater chance of rainfall.
A time series regression model will take into account the relationship between temperature and humidity, as well as other factors (for example, the location and elevation of the forecast location). The model then produces a prediction for the amount of rainfall (the target series), along with upper and lower bounds. For example, if the model predicts that there is a 90% chance of rain, and the upper bound for the amount of rainfall is 1 inch, then you might want to make sure that you have enough rain gear on hand.
Backcasts can be used to possibly improve the accuracy of forecasts for future time periods. The challenge with using regression to forecast is that the predictors' future values must be given. If, for example, temperature and humidity are the predictors, you need to know their future values on the same time scale as the rainfall series to make a forecast.
- How to Build Time Series Regression Models
Oracle exponential smoothing solves the problem of knowing future values on the same time scale as the target series by forecasting the predictor time series using exponential smoothing.
Related Topics
See Also:
Hyndman, R.J. and Athanasopoulos, G., Forecasting: Principles and Practice, 3rd edition, Department of Econometrics and Business Statistics, Monash University, VIC 3800, Australia, May 2021, Chapter 7
Parent topic: Time Series
14.5.1 How to Build Time Series Regression Models
Oracle exponential smoothing solves the problem of knowing future values on the same time scale as the target series by forecasting the predictor time series using exponential smoothing.
To build a regression model that predicts a future period, the correlated series must have a value in that future period. Hence, all correlated series must be forecast. Backcasts are included for the correlated series as smoothed versions of the correlated series values that can be used as input to the regression model. Backcasts are also available for the target series, as these are part of the standard output of an Oracle machine learning time series model. Target series backcasts can also be included in the regression model.
You can also create build and score datasets. The build data set contains the target series (forecast series), for example, rain; the backcasted target series, for example, backcasted rain; and the backcasted dependent series, for example, backcasted temperature and humidity. The backcasts and forecasts of the time series models can both be used as input to the regression model. The series all use the same time periods, so that the values of the target and the predictors co-occur.
The score data set follows the same schema as the build data set but provides forecasts as required for future values. The score data set can be supplied to the apply procedure of the regression model. Backcasts can be smoother and more structurally consistent with forecasts. The incremental improvement of the regression model over the baseline model can be seen in the backcast of the target series.
Because of the database's versatility, different time series regression variations are possible. A user can add factors such as holidays and environmental changes to the build and score data sets that account for categorical variables. In multiple time series regression, flag variables can be used to account for events or conditions that may have a significant impact on the dependent variable. For example, you might use a flag variable to indicate whether a particular day is a public holiday, or whether a particular month is a winter month. The inclusion of such factors in the model can improve the accuracy of the forecast by accounting for the impact of categorical variables on the dependent variable.
Holidays can be expressed as a binary value column (0s and
1s). For example, a national_holiday column can be
made that has a value of 1 for national holidays and a value of 0 at
other times. In a demand forecast, a perceived change in the
environment, like the introduction of a competitor's product, can
also be shown as a binary value column, with 0 for times before the
introduction and 1 for times after.
Furthermore, as a special case, if a user happens to know the future values of the dependent series, a user could replace the backcasts with the original values in the regression build procedure by creating a data set that joins to the original build table. This user-created data set replaces the build data set.
In the following example, a training, actual, and a test
data sets are created using the stock market data. A special case of
actual values are provided in the prediction data set to compare the
accuracy of ESM and regression. The variable prod
is a flag variable that accounts for categorical values. It
indicates a change in the environment such as an introduction of a
new product. The DM$VR<model_name> model
detail view provides details of the time series regression build
schema or the forecast of the target column.
Related Topics
Parent topic: Time Series Regression
14.6 Time Series Statistics
Learn to evaluate model quality by applying commonly used statistics.
As with other regression functions, there are commonly used statistics for evaluating the overall model quality. An expert user can also specify one of these figures of merit as criterion to optimize by the model build process. Choosing an optimization criterion is not required because model-specific defaults are available.
- Conditional Log-Likelihood
Log-likelihood is a figure of merit often used as an optimization criterion for models that provide probability estimates for predictions which depend on the values of the model’s parameters. - Mean Square Error (MSE) and Other Error Measures
Compute Mean Square Error (MSE) to evaluate forecast accuracy. Use others metrics for additional error assessment. - Irregular Time Series
Irregular time series are time series data where the time intervals between observed values are not equally spaced. - Build and Apply
Build a new time series model when new data arrives, producing statistics and forecasts during the build process.
Parent topic: Time Series
14.6.1 Conditional Log-Likelihood
Log-likelihood is a figure of merit often used as an optimization criterion for models that provide probability estimates for predictions which depend on the values of the model’s parameters.
The model probability estimates for the actual values in the training data then yields an estimate of the likelihood of the parameter values. Parameter values that yield high probabilities for the observed target values have high likelihood, and therefore indicate a good model. The calculation of log-likelihood depends on the form of the model.
Conditional log-likelihood breaks the parameters into two groups. One group is assumed to be correct and the other is assumed the source of any errors. Conditional log-likelihood is the log-likelihood of the latter group conditioned on the former group. For example, Exponential Smoothing (ESM) models make an estimate of the initial model state. The conditional log-likelihood of an ESM model is conditional on that initial model state (assumed to be correct). The ESM conditional log-likelihood is as follows:
where et is the error at time t and k(x(t-1) ) is 1 for ESM models with additive errors and is the estimated level at the previous time step in models with multiplicative error.
Parent topic: Time Series Statistics
14.6.2 Mean Square Error (MSE) and Other Error Measures
Compute Mean Square Error (MSE) to evaluate forecast accuracy. Use others metrics for additional error assessment.
The mean square error used as an optimization criterion, is computed as:
Note:
These "forecasts" are for over periods already observed and part of the input time series.Since time series models can forecast for each of multiple steps ahead, time series can measure the error associated with such forecasts. Average Mean Square Error (AMSE), another figure of merit, does exactly that. For each period in the input time series, it computes a multi-step forecast, computes the error of those forecasts and averages the errors. AMSE computes the individual errors exactly as MSE does taking cognizance of error type (additive or multiplicative). The number of steps, k, is determined by the user (default 3). The formula is as follows:
Other figure of merit relatives of MSE include the Residual Standard Error (RMSE), which is the square root of MSE, and the Mean Absolute Error (MAE) which is the average of the absolute value of the errors.
Parent topic: Time Series Statistics
14.6.3 Irregular Time Series
Irregular time series are time series data where the time intervals between observed values are not equally spaced.
One common practice is for the time intervals between adjacent steps to be equally spaced. However, it is not always convenient or realistic to force such spacing on time series. Irregular time series do not make the assumption that time series are equally spaced, but instead use the case id’s date and time values to compute the intervals between observed values. Models are constructed directly on the observed values with their observed spacing. Oracle time series analysis handles irregular time series.
Parent topic: Time Series Statistics
14.6.4 Build and Apply
Build a new time series model when new data arrives, producing statistics and forecasts during the build process.
Many of the Oracle Machine Learning for SQL functions have separate build and apply operations, because you can construct and potentially apply a model to many different sets of input data. However, time series input consists of the target value history only. Thus, there is only one set of appropriate input data. When new data arrive, good practice dictates that a new model be built. Since the model is only intended to be used once, the model statistics and forecasts are produced during model build and are available through the model views.
Parent topic: Time Series Statistics
14.7 Time Series Algorithm
Oracle Machine Learning uses Exponential Smoothing to forecast from time series data.
Related Topics
Parent topic: Time Series