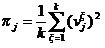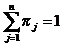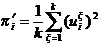12 CUR Matrix Decomposition
Learn how to use CUR decomposition based algorithm for attribute importance.
12.1 About CUR Matrix Decomposition
CUR Matrix Decomposition is a low-rank matrix decomposition algorithm that is explicitly expressed in a small number of actual columns and/or actual rows of data matrix.
CUR Matrix Decomposition was developed as an alternative to Singular Value Decomposition (SVD) and Principal Component Analysis (PCA). CUR Matrix Decomposition selects columns and rows that exhibit high statistical leverage or large influence from the data matrix. By implementing the CUR Matrix Decomposition algorithm, a small number of most important attributes and/or rows can be identified from the original data matrix. Therefore, CUR Matrix Decomposition is an important tool for exploratory data analysis. CUR Matrix Decomposition can be applied to a variety of areas and facilitates regression, classification, and clustering.
Related Topics
12.2 Singular Vectors
Singular Value Decomposition (SVD) is the first step in CUR Matrix Decomposition.
SVD returns left and right singular vectors for calculating column and row leverage scores. Perform SVD on the following matrix:
A ε RmxnThe matrix is factorized as follows:
A=UΣVTwhere U = [u1 u2...um] and V = [v1 v2...vn] are orthogonal matrices.
Σ is a diagonal m × n matrix with non-negative real numbers σ1,...,σρ on the diagonal, where ρ = min {m,n} and σξ is the ξth singular value of A.
Let uξ and vξ be the ξth left and right singular vector of A, the jth column of A can thus be approximated by the top k singular vectors and corresponding singular values as:
where vξj is the jth coordinate of the ξth right singular vector.
12.3 Statistical Leverage Score
Leverage scores are statistics that determine which column (or rows) are most representative with respect to a rank subspace of a matrix. The statistical leverage scores represent the column (or attribute) and row importance.
The normalized statistical leverage scores for all columns are computed from the top k right singular vectors as follows:
j = 1,...,n. Given that πj>=0 and
, these scores form a probability distribution over the n columns.
Similarly, the normalized statistical leverage scores for all rows are computed from the top k left singular vectors as:
where i = 1,...,m.
12.4 Column (Attribute) Selection and Row Selection
The CUR matrix decomposition in OML4SQL is designed for attribute and/or row importance. It returns attributes and rows with high importance that are ranked by their leverage (importance) scores. Column (Attribute) selection and row selection is the final stage in CUR Matrix Decomposition.
Attribute selection: Selects attributes with high leverage scores and reports their names, scores (as importance) and ranks (by importance).
Row selection: Selects rows with high leverage scores and reports their names, scores (as importance) and ranks (by importance).
-
CUR Matrix Decomposition first selects the jth column (or attribute) of A with probability
pj= min {1,cπj}for allj ε {1,...,n} -
If users enable row selection, select ith row of A with probability
pˊi = min {1,rπˊi}for alli ε {1,...,m} -
Report the name (or ID) and leverage score (as importance) for all selected attributes (if row importance is disabled) or for all selected attributes and rows (if row importance is enabled).
c is the approximated (or expected) number of columns that users want to select, and r is the approximated (or expected) number of rows that users want to select.
To realize column and row selections, you need to calculate the probability to select each column and row.
Calculate the probability for each column as follows:
pj = min {1,cπj}
Calculate the probability for each row as follows:
pˊi = min{1, cπˊi}.
A column or row is selected if the probability is greater than some threshold.
12.5 CUR Matrix Decomposition Algorithm Configuration
Configure the CUR Matrix Decomposition algorithm setting to build your model.
Create a model with the algorithm specific settings. Define the algorithm name as ALGO_CUR_DECOMPOSITION and mining function as ATTRIBUTE_IMPORTANCE.
See Also:
DBMS_DATA_MINING —Algorithm Settings: CUR Matrix Decomposition for a listing and explanation of the available model settings.Note:
The term hyperparameter is also interchangeably used for model setting.Row Selection
CURS_ROW_IMPORTANCE to CURS_ROW_IMP_ENABLE.
Note:
The row selection is performed only when users specify that row importance is enabled and the CASE_ID column is present.