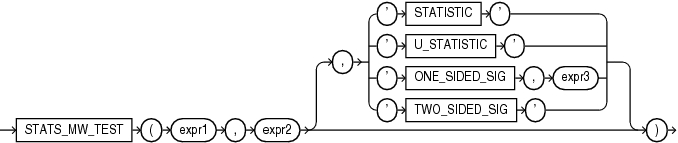
STATS_MW_TEST
Syntax
Purpose
A Mann Whitney test compares two independent samples to test the null hypothesis that two populations have the same distribution function against the alternative hypothesis that the two distribution functions are different.
The STATS_MW_TEST does not assume that the differences between the samples are normally distributed, as do the STATS_T_TEST_* functions. This function takes two required arguments: expr1 classifies the data into groups and expr2 contains the values for each of the groups. The optional third argument lets you specify the meaning of the NUMBER value returned by this function, as shown in Table 7-7. For this argument, you can specify a text literal, or a bind variable or expression that evaluates to a constant character value. If you omit the third argument, then the default is 'TWO_SIDED_SIG'.
See Also:
Appendix C in Oracle Database Globalization Support Guide for the collation determination rules for STATS_MW_TEST
Table 7-7 STATS_MW_TEST Return Values
| Argument | Return Value Meaning |
|---|---|
|
|
The observed value of Z |
|
|
The observed value of U |
|
|
One-tailed significance of Z |
|
|
Two-tailed significance of Z |
The significance of the observed value of Z or U is the probability that the variances are different just by chance—a number between 0 and 1. A small value for the significance indicates that the variances are significantly different. The degree of freedom for each of the variances is the number of observations in the sample minus 1.
The one-tailed significance is always in relation to the upper tail. The final argument, expr3, indicates which of the two groups specified by expr1 is the high value (the value whose rejection region is the upper tail).
STATS_MW_TEST computes the probability that the samples are from the same distribution by checking the differences in the sums of the ranks of the values. If the samples come from the same distribution, then the sums should be close in value.
STATS_MW_TEST Example
Using the Mann Whitney test, the following example determines whether the distribution of sales between men and women is due to chance:
SELECT STATS_MW_TEST
(cust_gender, amount_sold, 'STATISTIC') z_statistic,
STATS_MW_TEST
(cust_gender, amount_sold, 'ONE_SIDED_SIG', 'F') one_sided_p_value
FROM sh.customers c, sh.sales s
WHERE c.cust_id = s.cust_id;
Z_STATISTIC ONE_SIDED_P_VALUE
----------- -----------------
-1.4011509 .080584471