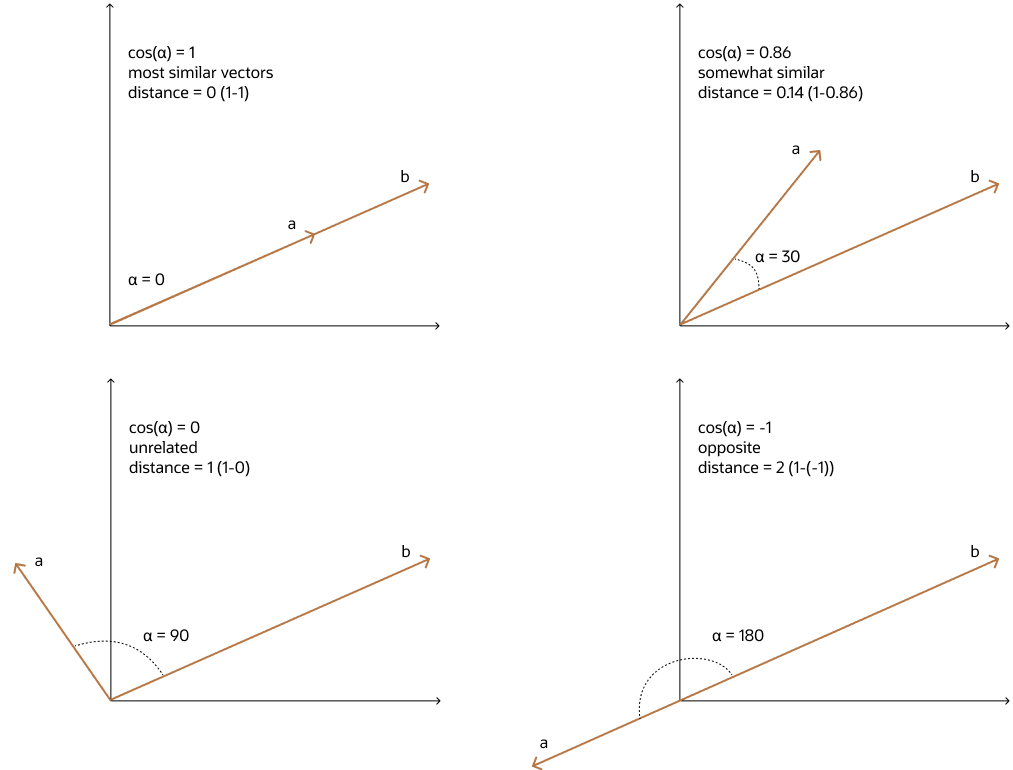
Cosine Similarity

One of the most widely used similarity metrics, especially in natural language processing (NLP), is cosine similarity, which measures the cosine of the angle between two vectors.

The smaller the angle, the more similar the two vectors. Cosine similarity measures the similarity in the direction or angle of the vectors, ignoring differences in their size (also called magnitude). The smaller the angle, the bigger its cosine. So, the cosine distance and the cosine similarity have an inverse relationship. While cosine distance measures how different two vectors are, cosine similarity measures how similar two vectors are.

The cosine similarity is calculated between two vectors, A and B, using the following formula:

cos(α) = (A · B) ÷ ( ||A|| * ||B||)

• A · B is the dot product of vectors A and B
• ||A|| is the magnitude (Euclidean norm) of vector A
• ||B|| is the magnitude (Euclidean norm) of vector B

The cosine distance is calculated by subtracting the cosine similarity from 1:

Distance(A, B) = 1 - cos(α)

Description of the illustration cosine_similarity_2x2.png