Logistic regression computations

  ShowHide

The Empirica Signal application offers two types of logistic regression: standard logistic regression and extended logistic regression. In standard logistic regression, users select an LR type of Standard on the Create Data Mining Run page. Extended logistic regression is performed when user select LR type of Extended.

Both models describe the relative weight of the presence of various drugs and other factors in a report in predicting the occurrence of a particular adverse event in the same report, but they provide different methods for fitting the model.

·        In the standard model, computations always use the same alpha value of 0.5. When the probability of an AE occurring is small, as in the case of a relatively rare AE, the result of the standard computation is an assumption that drug effects are more multiplicative than additive. If this assumption is false, logistic regression is likely to detect associations correctly, but the relative effects of drugs may not be correct. The standard model is equivalent to the logistic regression method found in statistics textbooks.

·        The extended logistic regression model allows an extended family of link functions that connect the estimated coefficients to the event probabilities. Whereas, the standard model assumes that this link function is the well-known S-shaped logistic curve, the extended model allows other shapes of curves, if another curve in the family fits the data better. The family is parameterized by the scalar alpha, where 0 < alpha < 1, and where alpha = 0.5 corresponds to the standard logistic. An interpretation of alpha is that value of the fitted event probability where the curve has a point of inflection, meaning that the curve is linear there and so the effects of multiple predictors are additive in the neighborhood of P(response event) = alpha. When the extended model option is chosen, the system estimates the maximum likelihood value of alpha and uses that value to form model predictions.

To compare scores calculated by each of these models, you can re-run a logistic regression data mining run that used one of these models and change only its LR type, name, and description for the second run.

The alpha value calculated for each response is available for review in the lr_coefficients.log file produced by the run.

To review this file:

1.         In the left navigation pane, hover on the Data Analysis icon (), then click Data Mining Runs.

2.         From the Row Action menu (), for the completed run, select View Jobs for Run.

3.         On the Jobs for Run page, click the LR_<number>_0 job, then at the bottom of the Job Detail page click lr_coefficients.log.

Logistic Regression

Logistic regression has long been a standard statistical tool for modeling how the probability of an event (the response) depends on multiple predictors. The estimated coefficients can be interpreted as the logarithm of an odds ratio. Especially for medical applications, where so much of statistical analysis consists of analysis of 2 x 2 frequency tables, the odds ratio, the simple ad/bc ratio, where (a, b, c, d) are the familiar counts in the 2 x 2 table examining the association of two values, has become a preferred measure of association. The preference for expressing associations in terms of odds ratios developed because the odds ratio is invariant to the choice of sampling plan of a study.

For example, consider a prospective study in which 1,000 patients are either exposed to a drug or not and then followed for signs of an adverse event such as irregular heartbeat. The data might look like this:

The risk ratio is (300/1000)/(100/1000), which equals 3.00.
The odds ratio is (300/700)/(100/900), which equals 3.86.

The risk ratio and the odds ratio are both large compared to the null hypothesis value of 1 that would be expected if there were no association between drug and irregular heartbeat. In other words, the probability (chance, risk) of irregular heartbeat is 3.00 times greater for patients taking the drug than for those not taking the drug. The odds (in favor) of irregular heartbeat are 3.86 times greater for patients taking the drug. This corresponds to a conversion between probabilities and odds. If a probability is p, the odds are p/(1-p), or if the odds are X:1 the probability is X/(X+1). Thus, odds of 3:1 mean that the probability is 3/4 = 0.75 and vice versa.

Consider now a retrospective study that has determined whether or not all those with irregular heartbeat took the drug, involving the same 400 patients as in the above table, but only 400 other patients with normal heartbeat are sampled instead of 1600. Without bias, the results looks like the following table, in which the Irregular column of the table is unchanged, and the counts in the Normal column have been divided by 4.

The risk ratio is (300/475)/(100/325), which equals 2.05.

The odds ratio is (300/175)/(100/225), which equals 3.86.

Note that the risk ratio has changed from 3.00 in the first table to 2.05 in the second table, while the odds ratio is unchanged at 3.86 in both tables. The odds ratio as a measure of association is invariant to multiplying either a row or a column of the 2x2 table by a constant. If the risk factor and the adverse event are each rare, then the risk ratio and the odds ratio are almost the same.

Consider the following table, where the Irregular column and the Drug row of the first table above have each been divided by 10 (so that the Irregular-Drug cell is reduced by a factor of 10x10=100).

The risk ratio is (3/73)/(10/910), which equals 3.74.

The odds ratio is (3/70)/(10/900), which equals 3.86.

Note that the risk ratio is now quite close to the still unchanged odds ratio of 3.86.

In many instances, a relatively small fraction of the population as a whole is exposed to a risk factor for an adverse event, and a relatively small fraction of the population actually suffers the adverse event. In such cases, you can loosely interpret the odds ratio as if it were a multiplier of the probability of the event rather than a multiplier of the odds of the event, since if p is small, p/(1-p) ~ p, so probabilities and odds are about the same. In such a case, even though you might have collected data that misestimates the proportion of those suffering the event by some unknown multiplier, and/or your data over- or under-samples those exposed to the risk by some other unknown factor, the odds ratio in your observed table may be a better estimate of the population risk ratio than the risk ratio computed from your 2x2 table, because the odds ratio is robust to bias in the row and column reporting rates. It is possible for a flawed data collection process to cause an excess frequency in just one cell of a table, without a corresponding increase in the other cell of its row or column. In that case, no measure of association from your data table is able to accurately measure the true association in the population.

Estimating odds ratios for multiple risk factors

It is common to collect data retrospectively when patients have been exposed to multiple risk factors. In such cases, you want obtain a measure of association between an adverse event and each of the risk factors, and separate out the associations with each risk factor. This can be a difficult task, especially when there are many risk factors that occur in multiple combinations across patients. No method of analysis is guaranteed to provide a best solution to this problem and, in fact, there may be no best answer, since interactions among the risk factors can create great ambiguities as to the interpretation of any association measures. However, ignoring such difficulties, the most common approach to this problem is logistic regression, which uses a multifactor analysis to compute a separate odds ratio for each risk factor.

In the ideal application of logistic regression, the odds ratio associated with multiple risk factors is the product of the estimated odds ratios for each of the risk factors being considered. For example, if one risk factor is being over age 65 (odds ratio = 1.5) and another is taking a particular drug (odds ratio = 2.0), then the logistic regression model assumes that the odds of having the adverse event are (1.5)(2.0) = 3.0 times as great for those over 65 who take the drug, compared to those under 65 who do not take the drug. The assumption that every risk factor's association with the adverse event can be summarized in a single odds ratio, and that simply multiplying them can describe the associations of multiple risk factors with the adverse event, is usually an oversimplification. Nevertheless, logistic regression has proven to be a very useful tool for summarizing associations among multiple risk factors and an event, and for finding those factors that seem to be consistently associated with the event no matter what other factors are present.

A typical logistic regression analysis produces a prediction equation of the form:

loge[p/(1-p)] = B0 + B1(Factor 1) + B2(Factor 2) + B3(Factor 3) + B4(Factor 4)

For example:

loge[p/(1-p)] = -5.0 + 1.1(Age > 65) + 0.6(Gender Male) + 0.3(Drug 1) + 0.8(Drug 2)

where loge[p/(1-p)] is the natural log of the odds of observing the adverse event, and the coefficients B0, B1, … are estimated from the database. The odds ratios for each factor are the exponentials of the coefficients. Therefore, in this example, the over 65 year age group has an odds ratio of e1.1 = 3.00 for the adverse event, males have an odds ratio of e0.6 = 1.82, and users of the two drugs have odds ratios of e0.3 = 1.35 and e0.8 = 2.23, respectively. The implicit assumption is that the combined odds ratio would be (3.00)(1.82)(1.35)(2.23) = 16.4 for males over 65 taking both drugs, compared to females under 65 taking neither drug. However, even when these complex associations are not estimated very exactly, the coefficients and their corresponding odds ratios often are good estimates of the relative overall strength of association of each factor with the adverse event. In this example, the association with age is greater than that of gender or of either drug.

Including potentially highly associated covariates in the computation is important, because otherwise the logistic regression might be subject to confounding due to the left-out covariates. For example, assume that (age > 65) was not in the model and that Drug1 was almost exclusively taken by the elderly in the database. In that situation, the estimated coefficient for Drug1 increases, since Drug1 is, in effect, a partial proxy for being elderly. The result might be an odds ratio for Drug 1 estimated to be 2 or 3 rather than the value 1.35 estimated when the variable (age > 65) is in the model, resulting in an inflated estimate of the association of Drug1 with the adverse event.

Specifying predictors

In general, it is important to include all covariates that might be associated with the adverse event as predictors in the logistic regression equation. For analysis of adverse event databases, Oracle recommends including covariate variables for age groups, gender, and report year, and explicitly including drugs that occur very frequently with the event. Drugs that occur most frequently with the event are, by their very frequency, more likely to be confounded with other drugs of interest in the database, and thereby cause biases if they are left out of the model. The logistic regression user interface makes it easy to enter all drugs in the data that occur more than a set number of times with the response event automatically, up to the defined maximum number of drugs allowed, including the drugs specifically requested.

Covariates must be categorical (stratification) variables having at least K > 1 categories, and every category value (K) must have at least one report with the response event present to be included. The covariate category having the most reports across all reports in the analysis is viewed as the standard for the odds ratio of each of the other categories.  If there are K categories for a covariate, there will be K-1 coefficients for that covariate, with a corresponding odds ratio for each coefficient. For example, if the categories for the Gender covariate are M, F, and U (for unknown), and if F is the most common gender category, then the output will only have odds ratios for M and for U. The odds ratio for M is the estimated reporting odds ratio comparing M to F, and the odds ratio for U is the estimated reporting odds ratio comparing U to F. Selecting the most common category to be used as the standard is arbitrary, but it allows you to interpret an odds ratio of 1 for a category as meaning that the selected category can be pooled with the most frequent category.

The logistic regression analysis provides a standard error for each coefficient that can be used to produce a confidence interval for each coefficient. The 90% confidence interval (CI) is computed as:

(estimated coefficient) +/- 1.645*(standard error of coefficient)

Taking the exponential of the endpoints of the coefficient CI produces a CI for the associated odds ratio. These are then labeled (LR05, LR95) in the logistic regression output tables.

To handle the relatively rare situation in which the most common category of a covariate has no reports with the response event (such as the most common gender category F and the event Prostate cancer), for that response a different category is selected as the most common. The computation does not leave out the gender covariate entirely in these situations as the confounding of gender with drugs taken primarily by one gender would distort the LOR estimates.

Each logistic regression data mining run generates a logistic regression log file (lr.log), that identifies the most common category found for each covariate. If any events in the run used a different category, the most common category for that event is noted.

Logistic regression models: standard and extended

Logistic regression (without explicit interaction terms) assumes that odds ratios (OR) are multiplicative in the presence of polypharmacy; that is, logistic regression predicts that a drug with OR=3 combined with a drug with OR=4 produces an OR=3*4=12 for the event of interest when both drugs are reported together. This simple relation holds for the OR scale but, for the probability scale, the predicted combined effect of risk factors is more complex. When the probabilities of events are in a middle range of 0.2 to 0.8, the joint effect of two risk factors on probabilities (according to standard logistic regression) is more additive than multiplicative.

For example, if the base rate (probability) for an event is 20%, the rate after applying an OR of 3 is 43%; the rate after applying an OR of 4 is 50%; and the rate after applying an OR of 12 is 75%. Compare these three rates to the original rate both as rate differences and as rate ratios:

Base rate = 0.20                  Rate difference                  Rate ratio____

Risk factor with OR=3:         .43 - .20 = .23                   .43/.20 = 2.15

Risk factor with OR=4:         .50 - .20 = .30                   .50/.20 = 2.50

Both factors with OR=12:     .75 - .20 = .55                   .75/.20 = 3.75

Thus, the combination of the two risk factors (if the odds ratios multiply) is more nearly additive than multiplicative on the probability scale, since .23 + .30 = .53 is close to .55, whereas 2.15*2.50 = 5.38 is not as close to 3.75.

On the other hand, suppose the base rate were 0.002, which is more in the range of most adverse event probabilities. In this case, applying odds ratios of 3, 4, and 12 results in probabilities of 0.0060, 0.0079, and 0.0234, respectively. Comparing rate differences to rate ratios in the low base rate example:

Base rate = 0.0020               Rate difference                  Rate ratio_______

Risk factor with OR=3:         .0060 - .0020 = .0040        .0060/.0020 = 3.00

Risk factor with OR=4:         .0079 - .0020 = .0059        .0079/.0020 = 3.95

Both factors with OR=12:     .0234 - .0020 = .0214        .0234/.0020 = 11.7

In this case, the effect of both factors is more multiplicative than additive on the probability scale, since .0040 + .0059 = .0099 is not as close to .0214, whereas 3.00*3.95 = 11.85 is close to 11.7.

In summary, logistic regression makes the following assumptions: the joint risk of two risk factors is nearly additive on the probability scale if the base rate is relatively large (e.g., about 0.2), but is nearly multiplicative if the base rate is very small (e.g., about 0.002). When modeling spontaneous reports, you are considering relative reporting ratios in a database of reports rather than risk. The question remains, which is more likely to fit spontaneous report ratios better? An additive model or a multiplicative model? Since most individual adverse events occur in a very small proportion of spontaneous reports, applying standard logistic regression fits the data well if the multiplicative model is approximately true.

To allow for the possibility that a nearly additive model for spontaneous report ratios might fit better than a nearly multiplicative model, the Empirica Signal application provides an alternative model called extended logistic regression. This family of models has a parameter, denoted (alpha), that specifies the region of near-additivity to be centered at an arbitrary base rate. If = 0.5, then extended logistic regression reduces to standard logistic regression. If you select the extended option, then the system performs an estimation of the best coefficients for each of many values of , and selects the value of that gives the best fit to the observed data.

If the estimated value of is near 0.5, this means that the standard logistic regression fits the data (that is, predicts the presence or absence of the response for individual reports) about as well as the extended logistic model. In practice, if the estimate of is between 0.4 and 0.6, then the odds ratio estimates for individual predictors is close to the corresponding estimates for standard logistic regression. In such a case, for simplicity in explaining your methodology to someone unfamiliar with extended LR, use the standard LR estimates. Another approach to choosing between standard and extended LR is to compare the difference ( - 0.5) to the standard error of . You can compute:

(Z-score for ) = ( - 0.5)/(standard error of )

If the Z-score is less than -3 or greater than +3, there is strong statistical evidence that extended LR fits the data better than standard LR.

The estimates of and their standard errors (separate estimates for each response value in the run) can be found in the Logistic regression coefficients log file (lr_coefficients.log) that is produced for each logistic regression data mining run.

It is difficult to say in advance whether extended LR fits any particular data much better than standard LR. Different response events give different choices. It takes more computation time to find the best fitting , so, if you want to get quicker answers for hundreds or thousands of response events, selecting standard LR accomplish that. But, in most situations, the estimation and examination of the values of and its standard errors, using extended LR, are recommended. If the data being used in the LR is voluminous, the standard error of may be very small; perhaps just 0.01 or even smaller. Then, even if is near 0.5, there may be strong evidence that it is not exactly 0.5. For example, if = 0.41, standard error =0.005, then the Z-score is 18, but the individual estimated odds ratios do not differ much from those of standard LR.

Two caveats apply to this model selection problem. First, even if one model fits the spontaneous reports better, there is still no guarantee that the resulting estimated odds ratios for each drug are valid estimates of the prospective risk to takers of the drug of an adverse reaction. Second, even in terms of fit to the relative reporting ratios, the better fitting model is not necessarily a perfect guide to which of the many drugs in the regression model are truly significant. If there are 100 drugs in the model, it may be that extended logistic regression fits better than standard logistic regression because it models the polytherapy effects involving 80 of the drugs better, while modeling those involving the other 20 drugs worse. That is, many of the drugs may combine in their effects additively, while others combine multiplicatively (or, in some more complicated combining formula), so that neither model can estimate the effects of every drug reliably. As statisticians often say, "no model is perfect, but many are useful."

The extended model is technically described as a binomial regression with a different link function. Suppose that z = B0 + B1X1 + B2X2 + … is the linear combination used for prediction, where the Bs are coefficients and the Xs are predictors. The standard logistic regression defines the probability of event occurrence as p(z), where:

p(z) = 1/(1 + exp(-z))

Extended logistic regression uses the formula:

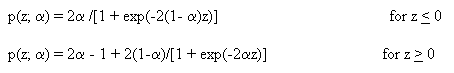
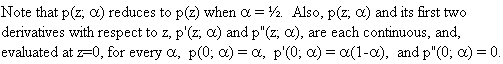
A two-dimensional plot of the probability distribution function of the extended logistic regression computation follows:

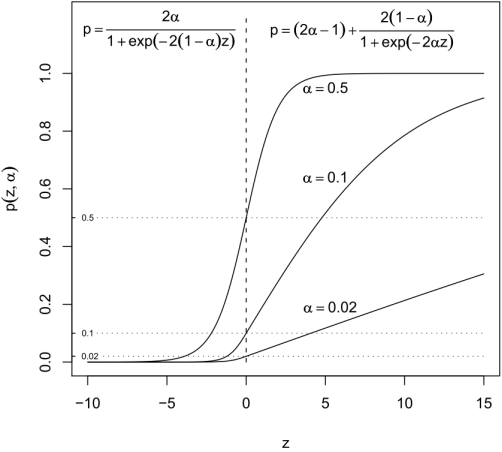
For a predictor X whose standard LR coefficient is B, the odds ratio comparing the probabilities of the event at X = 0 versus X = 1 is OR = eB. In the case of extended logistic regression with estimated link parameter , the odds ratio is defined as:

OR = (1 – p0) p(z0 + B, ) / p0 (1 – p(z0 + B, ))

Where p0 = (# response events)/(# Reports) [proportion of reports with the response event] and z0 is the solution to the equation  p(z0 + B, ) = p0.

This formula for OR reduces to eB when = ½. The 90% confidence intervals for OR are computed by replacing B in the above formula by B +/- 1.645*standard error(B), analogous to the procedure for standard logistic regression.

Each logistic regression data mining run generates a tab-delimited log file, lr_coefficients.log, with the alpha value computed for each response and its standard error. When you define options for the run, you can check Save coefficients to include the coefficient and standard error calculated for each predictor and response in this log.

For more information about logistic regression, see any intermediate-level statistics or biostatistics textbook, such as Statistical Methods in Epidemiology by HA Kahn and CT Sempos, Oxford U Press, 1989.