18 Configuring Oracle Mediator Service Components and Engines
This chapter includes the following sections:
For more information about Oracle Mediator tuning and performance properties, see Tuning Performance.
18.1 Configuring Oracle Mediator Service Engine Properties
Mediator service engine properties are used by the Mediator service engine during processing of Mediator service components.
To configure Mediator service engine properties:
-
Access the Mediator Service Engine Properties page using one of the following methods:
From the SOA Infrastructure Menu... From the SOA Folder in the Navigator... -
Select SOA Administration > Mediator Properties.
-
Right-click soa-infra.
-
Select SOA Administration > Mediator Properties.
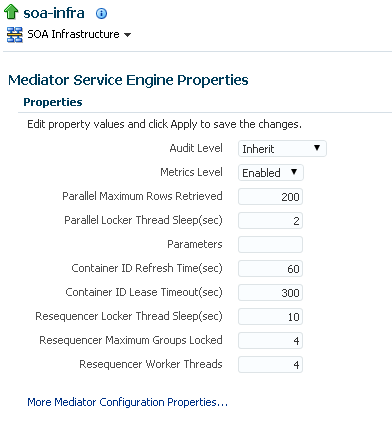
The Mediator Service Engine Properties page displays a list of Mediator properties, as shown in the following figure.
-
-
Make changes to the service engine properties that are appropriate to your environment.
The properties are described in Table 18-1 below.
Table 18-1 Mediator Service Engine Properties
Property Description Audit Level
The Mediator-specific audit level. The value of this property overrides the value of the global SOA Infrastructure audit level property. The possible values of this property are:
-
Off: Switches off auditing for Mediator. Business flow instance tracking and payload tracking information are not collected.
-
Inherit: The level of audit is the same as the SOA infrastructure. This setting enables the Mediator audit level to automatically change, when the global setting is changed. Setting a different audit level tracking, for this page, overrides the tracking set at the SOA Infrastructure level.
-
Production: All events are logged. All audit details, except the details of assign activities, are logged. Instance tracking information is collected, but payload details are not captured and these details are not available in the flow audit trails. This level is optimal for most typical operations and testing.
-
Development: All events and all audit details are logged. In addition, payload details are captured and are available in the flow audit trails. This level is useful for debugging purposes, but may impact performance.
The default value of this flag is Inherit.
Notes:
-
You do not need to restart the server after changing these properties.
-
Audit levels were known as instance tracking levels in the Oracle Application Server 10g releases.
Metrics Level
The Mediator-specific property for configuring the Dynamic Monitoring Service (DMS) metrics level. DMS metrics are used to measure the performance of application components. The possible values of this property are:
-
Enabled: Enables DMS metrics tracking
-
Disabled: Disables DMS metrics tracking
Parallel Maximum Rows Retrieved
The number of rows retrieved per iteration for parallel processing.
Note: A large value for this property can result in memory exhaustion.
Parallel Locker Thread Sleep (sec)
The idle time between two successive iterations for retrieving rows, when there is no message for parallel processing. The time is measured in seconds.
Parameters
Custom configuration properties. For an example, see Configuring Resequenced Messages.
Container ID Refresh Time (sec)
Container ID Lease Timeout (sec)
Heartbeat infrastructure properties. The heartbeat infrastructure is a part of the Mediator service engine and detects the absence of a Mediator service engine instance due to failure or shutdown of a node. The heartbeat infrastructure creates a unique identifier for each instance of the Mediator service engine and performs the necessary housekeeping tasks, if a Mediator service engine fails. The heartbeat infrastructure consists of a heartbeat thread. The heartbeat thread periodically updates the time stamp associated with each Mediator service engine's unique identifier. By updating the time stamp associated with it, a Mediator service engine announces its presence to the other Mediator service engines. The heartbeat thread also checks if there are unique identifiers that have not been updated for a particular period. You can configure the heartbeat framework by setting the following parameters:
-
Container ID Refresh Time (sec): The time interval at which the heartbeat thread periodically updates the time stamp associated with each Mediator service engine's unique identifier.
Notes: The default value is
60seconds. In case of unplanned outages, you must wait the amount of time specified for this property after restarting the server.You can set this parameter to a smaller value, like
30seconds, if you need to ensure more frequent refreshes. -
Container ID Lease Timeout (sec): The time interval at which the heartbeat thread periodically checks if there are unique identifiers that have not been updated for a particular period. A node is considered to be timed out if it has not refreshed itself for a duration longer than the amount of time specified here.
Notes: The default value is
300seconds. You can set this parameter to a larger value, like600seconds, if you find your nodes being timed out because of slow-running SQL statements, for example.
By configuring these parameters, you can specify the period used by the heartbeat thread to detect the failure of a Mediator service engine.
Resequencer Locker Thread Sleep (sec)
The sleep interval for the locker threads in seconds. When the resequencer is unable to find a group with messages that can be processed, the locker thread sleeps for the specified duration. The locker thread does not sleep between each iteration of a database seek, as long as it finds groups with messages that can be processed. The default value is 10.
Resequencer Maximum Groups Locked
The number of groups to be retrieved for processing in a single iteration of a database seek. Once retrieved, the groups are assigned to worker threads for processing. The default value is 4.
Resequencer Worker Threads
The number of worker threads (dispatchers) for processing resequencing groups in parallel. Each worker thread is assigned a group, and then processes messages for the group in sequence. When there are a large number of groups waiting for messages to be processed, increasing this parameter can improve performance.The default value is 4.
-
-
To configure advanced Mediator properties in the System MBean Browser, click More Mediator Configuration Properties.
You can also access Mediator properties in the System MBean Browser through the navigator, as described below.
18.1.1 To Access System MBean Browser Properties:
-
From the SOA Infrastructure menu, point to Administration and then select System MBean Browser.
The System MBean Browser page appears.
-
In the System MBean Browser navigation pane on the left, expand oracle.as.soainfra.config, expand Server: server_name, expand MediatorConfig, and then select mediator.
The properties of the MBean appear in the right pane.
-
To change the value of a property, modify its Value field and then click Apply.
Note:
Not all values can be modified. The System MBean properties generally correspond to the properties listed inTable 18-1, with some additional read-only properties for the MBean. An additional property, ContainerInitRetries, is not listed in Table 18-1. This property indicates the number of attempts that are made to create an Oracle Mediator service engine instance ID.
18.2 Configuring Resequenced Messages
For Mediator service components to resequence messages, you must configure the following:
-
The worker thread count
-
The maximum number of groups that can be locked by a thread
-
The sleep interval
If the Mediator service component is configured to use best effort resequencing and the messages to process in each batch are based on a time window rather than a maximum number of rows, you can also configure the buffer window.
To configure resequenced messages: