


Java 3D API Specification



Java 3D API Specification
C H A P T E R 3 3 |
|
Scene Graph Superstructure |
JAVA 3D's superstructure consists of one or more VirtualUniverse objects, each of which contains a set of one or more high-resolution Locale objects. The Locale objects, in turn, contain collections of subgraphs that comprise the scene graph (see Figure 3-1).
3.1
Java 3D defines the concept of a virtual universe as a three-dimensional space with an associated set of objects. Virtual universes serve as the largest unit of aggregate representation, and can also be thought of as databases. Virtual universes can be very large, both in physical space units and in content. Indeed, in most cases a single virtual universe will serve an application's entire needs.The Virtual Universe
Virtual universes are separate entities in that no node object may exist in more than one virtual universe at any one time. Likewise, the objects in one virtual universe are not visible in, nor do they interact with objects in, any other virtual universe.
To support large virtual universes, Java 3D introduces the concept of Locales that have high-resolution coordinates as an origin. Think of high-resolution coordinates as "tie-downs" that precisely anchor the locations of objects specified using less precise floating-point coordinates that are within the range of influence of the high-resolution coordinates.
A Locale, with its associated high-resolution coordinates, serves as the next level of representation down from a virtual universe. All virtual universes contain one or more high-resolution-coordinate Locales, and all other objects are attached to a Locale. High-resolution coordinates act as an upper-level translation-only transform node. For example, the coordinates of all objects attached to a particular Locale are all relative to the location of that Locale's high-resolution coordinates.
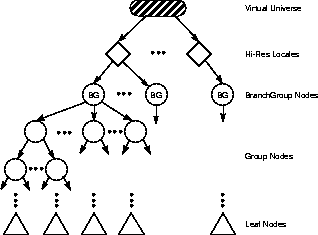
Figure 3-1
The Virtual Universe
While a virtual universe is similar to the traditional computer graphics concept of a scene graph, a given virtual universe can become so large that it is often better to think of a scene graph as the descendent of a high-resolution-coordinate Locale.
3.2
To construct a three-dimensional scene, the programmer must execute a Java 3D program. The Java 3D application must first create a VirtualUniverse object and attach at least one Locale to it. Then the desired scene graph is constructed, starting with a BranchGroup node and including at least one ViewPlatform object, and is attached to the Locale. Finally, a View object is constructed that references the ViewPlatform object (see Section 1.6, "Structuring the Java 3D Program"). As soon as a scene graph containing a ViewPlatform is attached to the VirtualUniverse, Java 3D's rendering loop is engaged, and the scene will appear on the drawing canvas(es) associated with the View object.Establishing a Scene
3.3
Java 3D is a runtime application programming interface (API), not a file format. As an API, Java 3D provides no direct mechanism for loading or storing a virtual universe. Constructing a scene graph involves the execution of a Java 3D program. However, loaders to convert a number of standard 3D file formats to or from Java 3D virtual universes are expected to be generally available.Loading a Virtual Universe
3.4
By default, Java 3D coordinate systems are right-handed, with the orientation semantics being that +Y is the local gravitational up, +X is horizontal to the right, and +Z is directly toward the viewer. The default units are meters.Coordinate Systems
3.5
Double-precision floating-point, single-precision floating-point, or even fixed-point representations of three-dimensional coordinates are sufficient to represent and display rich 3D scenes. Unfortunately, scenes are not worlds, let alone universes. If one ventures even a hundred miles away from the (0.0, 0.0, 0.0) origin using only single-precision floating-point coordinates, representable points become quite quantized, to at very best a third of an inch (and much more coarsely than that in practice).High-resolution Coordinates
To "shrink" down to a small size (say the size of an IC transistor), even very near (0.0, 0.0, 0.0), the same problem arises.
If a large contiguous virtual universe is to be supported, some form of higher-resolution addressing is required. Thus the choice of 256-bit positional components for "high-resolution" positions.
3.5.1
Java 3D high-resolution coordinates consist of three 256-bit fixed-point numbers, one each for x, y, and z. The fixed point is at bit 128, and the value 1.0 is defined to be exactly 1 meter. This coordinate system is sufficient to describe a universe in excess of several hundred billion light years across, yet still define objects smaller than a proton (down to below the planck length). Table 3-1 shows how many bits are needed above or below the fixed point to represent the range of interesting physical dimensions.Java 3D High-resolution Coordinates
A 256-bit fixed-point number also has the advantage of being able to directly represent nearly any reasonable single-precision floating-point value exactly.
High-resolution coordinates in Java 3D are only used to embed more traditional floating point coordinate systems within a much higher-resolution substrate. In this way a visually seamless virtual universe of any conceivable size or scale can be created, without worry about numerical accuracy.
3.5.2
Within a given virtual world coordinate system, positions are expressed by three floating point numbers. The virtual world coordinate scale is in meters, but this can be affected by scale changes in the object hierarchy.Java 3D Virtual World Coordinates
3.5.3
High-resolution coordinates are represented as signed, two's-complement, fixed-point numbers consisting of 256 bits. Although Java 3D keeps the internal representation of high-resolution coordinates opaque, users specify such coordinates using 8-element integer arrays. Java 3D treats the integer found at index 0 as containing the most significant bits and that found at index 7 as containing the least significant bits of the high-resolution coordinate. The binary point is located at bit position 128, or between the integers at index 3 and 4. A high-resolution coordinate of 1.0 is 1 meter.Details of High-resolution Coordinates
The semantics of how file loaders deal with high-resolution coordinates is up to the individual file loader, as Java 3D does not directly define any file-loading semantics. However, some general advice can be given (note that this advice is not officially part of the Java 3D specification).
For "small" virtual universes (on the order of hundreds of meters across in relative scale), a single Locale with high-resolution coordinates at location (0.0, 0.0, 0.0) as the root node (below the VirtualUniverse object) is sufficient; a loader can automatically construct this node during the loading process, and the point in high-resolution coordinates does not need any direct representation in the external file.
Larger virtual universes are expected to be usually constructed like computer directory hierarchies, that is, as a "root" virtual universe containing mostly external file references to embedded virtual universes. In this case, the file reference object (user-specific data hung off a Java 3D group or hi-res node) defines the location for the data to be read into the current virtual universe.
The data file's contents should be parented to the file object node while being read, thus inheriting the high-resolution coordinates of the file object as the new relative virtual universe origin of the embedded scene graph. If this scene graph itself contains high-resolution coordinates, it will need to be offset (translated) by the amount in the file object's high-resolution coordinates, and then added to the larger virtual universe as new high-resolution coordinates, with their contents hung off below them. Once again, the above procedure is not part of the official Java 3D specification, but some more details on the care and use of high-resolution coordinates in external file formats will probably be available as a Java 3D application note.
Authoring tools that directly support high-resolution coordinates should create additional high-resolution coordinates as a user creates new geometry "sufficiently" far away (or of different scale) from existing high-resolution coordinates.
Semantics of widely moving objects. Most fixed and nearly-fixed objects stay attached to the same high-resolution Locale. Objects that make wide changes in position or scale may need to be periodically reparented to more appropriate high-resolution Locale. If no appropriate high-resolution Locale exists, the application may need to create a new one.
Semantics of viewing. The ViewPlatform object and the associated nodes in its hierarchy are very often widely moving objects. Applications will typically attach the view platform to the most appropriate high-resolution Locale. For display, all objects will first have their positions translated by the difference between the location of their high-resolution Locale, and the view platform's high-resolution Locale. (In the common case of the Locales being the same, no translation is necessary.)
3.6
This section describes the API for the VirtualUniverse, Locale, and HiResCoord objects.API for Superstructure Objects
3.6.1
The VirtualUniverse object consists of a set of Locale objects.VirtualUniverse Object
Constructors
The VirtualUniverse object has the following constructors.public VirtualUniverse()This constructs a new VirtualUniverse object. This VirtualUniverse can then be used to create Locale objects.
Methods
The VirtualUniverse object has the following methods.public final Enumeration getAllLocales() public final int numLocales()The first method returns the Enumeration object of all Locales in this virtual universe. ThenumLocalesmethod returns the number of Locales.
3.6.2
The Locale object consists of a point, specified using high-resolution coordinates, and a set of subgraphs, rooted by BranchGroup node objects.Locale Object
Constructors
The Locale object has the following constructors.public Locale(VirtualUniverse universe) public Locale(VirtualUniverse universe, int x[], int y[], int z[]) public Locale(VirtualUniverse universe, HiResCoord hiRes)These three constructors create a new high-resolution Locale object in the specified VirtualUniverse. The first form constructs a Locale object located at (0.0, 0.0, 0.0). The other two forms construct a Locale object using the specified high-resolution coordinates. In the second form, the parametersx,y, andzare arrays of eight 32-bit integers that specify the respective high-resolution coordinate.
Methods
The Locale object has the following methods. For the Locale picking methods, see Section 10.3.2, "BranchGroup Node and Locale Node Pick Methods."public VirtualUniverse getVirtualUniverse()This method retrieves the virtual universe within which this Locale object is contained.public void setHiRes(int x[], int y[], int z[]) public void setHiRes(HiResCoord hiRes) public void getHiRes(HiResCoord hiRes)These methods set or get the high-resolution coordinates of this Locale.public void addBranchGraph(BranchGroup branchGroup) public void removeBranchGraph(BranchGroup branchGroup) public void replaceBranchGraph(BranchGroup oldGroup, BranchGroup newGroup) public int numBranchGraphs() public Enumeration getAllBranchGraphs()The first three methods add, remove, and replace a branch graph in this Locale. Adding a branch graph has the effect of making the branch graph "live." The fourth method retrieves the number of branch graphs in this Locale. The last method retrieves an Enumeration object of all branch graphs.
3.6.3
A HiResCoord object defines a point using a set of three high-resolution coordinates, each of which consists of three two's-complement fixed-point numbers. Each high-resolution number consists of 256 total bits with a binary point at bit 128. Java 3D uses integer arrays of length eight to define or extract a single 256-bit coordinate value. Java 3D interprets the integer at index 0 as the 32 most significant bits and the integer at index 7 as the 32 least significant bits.HiResCoord Object
Constructors
The HiResCoord object has the following constructors.public HiResCoord(int x[], int y[], int z[]) public HiResCoord(HiResCoord hc) public HiResCoord()The first constructor generates the high-resolution coordinate point from three integer arrays of length eight. The integer arrays specify the coordinate values corresponding with their name. The second constructor creates a new high-resolution coordinate point by cloning the high-resolution coordinateshc. The third constructor creates new high-resolution coordinates with value (0.0, 0.0, 0.0).public void setHiResCoord(int x[], int y[], int z[]) public void setHiResCoord(HiResCoord hiRes) public void setHiResCoordX(int x[]) public void setHiResCoordY(int y[]) public void setHiResCoordZ(int z[])These five methods modify the value of high-resolution coordinatesthis. The first method resets all three coordinate values with the values specified by the three integer arrays. The second method sets the value ofthisto that of high-resolution coordinateshiRes. The third, fourth, and fifth methods reset the corresponding coordinate ofthis.public void getHiResCoord(int x[], int y[], int z[]) public void getHiResCoord(HiResCoord hc) public void getHiResCoordX(int x[]) public void getHiResCoordY(int y[]) public void getHiResCoordZ(int z[])These five methods retrieve the value of the high-resolution coordinatesthis. The first method retrieves the high-resolution coordinates' values and places those values into the three integer arrays specified. All three arrays must have length greater than or equal to eight. The second method updates the value of the high-resolution coordinateshcto match the value ofthis. The third, fourth, and fifth methods retrieve the coordinate value that corresponds to their name and update the integer array specified, which must be of length eight or greater.public void add(HiResCoord h1, HiResCoord h2) public void sub(HiResCoord h1, HiResCoord h2)These two methods perform arithmetic operations on high-resolution coordinates. The first method addsh1toh2and stores the result inthis. The second method subtractsh2fromh1and stores the result inthis.public void scale(int scale, HiResCoord h1) public void scale(int scale)These methods scale a high-resolution coordinate point. The first method scalesh1by the scalar valuescaleand places the scaled coordinates intothis. The second method scalesthisby the scalar valuescaleand places the scaled coordinates back intothis.public void negate(HiResCoord h1) public void negate()These two methods negate a high-resolution coordinate point. The first method negatesh1and stores the result inthis. The second method negatesthisand stores its negated value back intothis.public void difference(HiResCoord h1, Vector3d v)This method subtractsh1fromthisand stores the resulting difference vector in the double-precision floating-point vectorv. Note that although the individual high-resolution coordinate points cannot be represented accurately by double-precision numbers, this difference vector between them can be accurately represented by doubles for many practical purposes, such as viewing.public boolean equals(HiResCoord h1) public boolean equals(Object o1)The first method performs an arithmetic comparison betweenthisandh1. It returnstrueif the two high-resolution coordinate points are equal; otherwise, it returnsfalse. The second method returns true if the Objecto1is of type HiResCoord and all of the data members ofo1are equal to the corresponding data members in this HiResCoord.public double distance(HiResCoord h1)This method computes the linear distance between high-resolution coordinate pointsthisandh1, and returns this value expressed as a double. Note that although the individual high-resolution coordinate points cannot be represented accurately by double precision numbers, this distance between them can be accurately represented by a double for many practical purposes.



Java 3D API Specification
Copyright © 1999, Sun Microsystems, Inc. All rights reserved.