Sun S3L FFT Optimizations

The Sun S3L FFT is optimized for use by message-passing applications. It works for S3L arrays with arbitrary distributions a multiprocess process grid. For certain data distributions, maximum efficiency can be obtained.

For example, the algorithm used for a two-dimensional complex-to-complex parallel FFT is optimized for arrays distributed along their second dimension, where the number of processes is a power of two. For maximum efficiency, both axes of the array must be divisible by the number of processes.

When the array distribution allows fast algorithms to be used, the two-dimensional FFT consists essentially of multiple one-dimensional FFTs performed along the array columns local to the process. It then transposes the array in such a way that each process has a number of local rows. This is followed by a second set of local one-dimensional FFTs. Finally, the data are transposed back to the original distribution.

This sequence is illustrated by the diagrams in Figure 3-3 through Figure 3-5.

Figure 3-3 Phase 1 of Two-Dimensional FFT Performing Independent One-Dimensional FFT

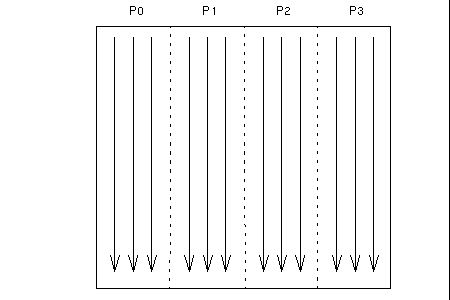
Figure 3-4 Phase 2 of Two-Dimensional FFT Performing Local Transpositions

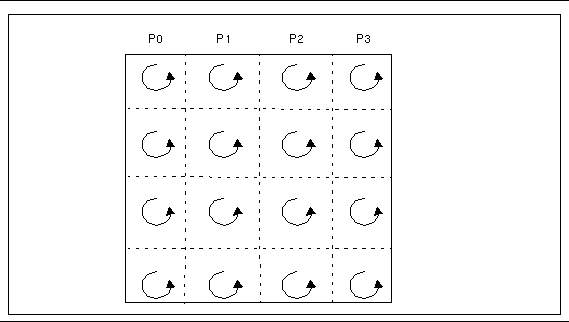
Figure 3-5 Phase 3 of Two-Dimensional FFT Performing Global Transpositions

When the data are distributed in suboptimal ways-- for example, along both dimensions on a rectangular process-grid--a global communication step is usually performed first to redistribute the data to its optimal distribution and then the optimized FFT is performed. This redistribution step increases execution overhead.