Interval Arithmetic Programming Reference

Glossary

affirmative relation

An order relation other than certainly, possibly, or set not equal. Affirmative relations affirm something, such as a < b.

affirmative relational operators

An affirmative relational operator is an element of the set: {<, , =, , >}.

anti-affirmative relation

An anti-affirmative relation is a statement about what cannot be true. The order relation is the only anti-affirmative relation in Fortran.

anti-affirmative relational operator

The Fortran .NE. and /= operators implement the anti-affirmative relation. The certainly, possible, and set versions for interval operands are denoted .CNE., .PNE., and .SNE., respectively.

assignment statement

An assignment statement is a Fortran statement having the form: V = expression. The left-hand side of the assignment statement is the variable, array element, or array, V.

certainly true
relational operator

See relational operators: certainly true.

closed interval

A closed interval includes its endpoints. A closed interval is a closed set. The interval [2, 3] = {z | 2 z 3} is closed, because its endpoints are included. The interval (2, 3) = {z | 2 < z < 3} is open, because its endpoints are not included. Interval arithmetic, as implemented in f95, only deals with closed intervals.

closed mathematical system

In a closed mathematical system, there can be no undefined operator-operand combinations. All defined operations on elements of a closed system must produce elements of the system. The real number system is not closed, because division by zero is undefined in this system.

closed set

A closed set contains all limit or accumulation points in the set. That is, given the set, S, and sequences, , the closure of S is , where denotes an accumulation or limit point of the sequence {s_j}.

The set of real numbers is the open set {z | - < z < +}, because it does not include - and +. The set of extended real numbers, , is closed.

closure-composition equality

Given the expressions f, g, and h, with

,

the closure-composition equality states that

.

The closure of at the point x₀ is equal to the composition of its component's closures, and .

closure of expression

The closure of the expression f of n-variables, evaluated over the set is denoted , and for is defined:

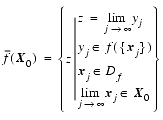
For .

The accumulation points, x_j, of all sequences, { }, are elements of the set, X₀. The closure of f is the set of all possible accumulation points of f given the conditions on the right-hand side of the above defining expression are satisfied.

is defined for all .

connected set

The connected set of numbers between and including two values, a b, contains all the values between and including a and b.

composite expression

Forming a new expression, f, (the composite expression) from the given expressions, g and h by the rule f({ }) = g(h({ })) for all singleton sets, { } = {x₁}  {x_n} in the domain of h for which h is in the domain of g. Singleton set arguments connote the fact that expressions can be either functions or relations.

constant expression

A constant expression in Fortran contains no variables or arrays. It can contain constants and operands. The expression [2, 3] + [4, 5] is a constant expression. If X is a variable, the expression X + [2, 3] is not a constant expression. If Y is a named constant, Y + [2, 3] is a constant expression.

containment constraint

The containment constraint on the interval evaluation, f([x]), of the expression, f, at the degenerate interval, [x], is:

f([x]) cset(f,{x}),

where cset(f,{x}) denotes the containment set of all possible values that f([x]) must contain. Because the containment set, cset(x ÷ y, {(1, 0)}) = {-, +}, [1] / [0] = hull({-, +}) = [-, +]. See also containment set.

containment failure

A containment failure is a failure to satisfy the containment constraint. For example, a containment failure results if [1]/[0] is defined to be [empty]. This can be seen by considering the interval expression

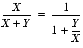
for X=[0] and Y, given . The containment set of the first expression is [0]. However, if [1]/[0] is defined to be [empty], the second expression is also [empty]. This is a containment failure.

containment set

The containment set, cset(h, {x}), of the expression h is the smallest set that does not violate the containment constraint when h is used as a component of any composition, f({x}) = g(h({x}), {x}).

For h(x, y) = x ÷ y,

cset(h, {(+, +)}) = [0, +].

See also cset(expression, set).

containment set closure identity

Given any expression f({x}) = f({x₁} {x_n}) of n-variables and the point, x₀, then cset(f, {x₀}) = f({x₀}), the closure of f at the point, x₀.

containment set equivalent

Two expressions are containment-set equivalent if their containment sets are everywhere identical.

containment set evaluation theorem

Let eval(f, {x}) denote the code-list evaluation of the expression f, using individual composition closures to compute the value of every sub-expression, whether it is the value of an operation, function, or relation. Given the expression, f({x}) = f({x₁} {x_n}), whether f is a function or a relation, then for all , cset(f, {x₀}) eval(f, {x₀}).

context-dependent INTERVAL constant

The internal approximation of an INTERVAL constant under widest-need expression processing is context dependent, because it is a sharp interval with KTPV that equals KTPV_max. Any approximation for the interval constant [a, b] can be used, provided,

[a,b] ev([a,b]),

where ev([a,b]) denotes the external value of the interval constant, [a, b]. Choosing any internal approximation is permitted, provided containment is not violated. For example, the internal approximations, [0.1_4], [0.1_8], and [0.1_16], all have external value, ev(0.1) = 1/10, and therefore do not violate the containment constraint. Under widest-need expression processing the internal approximation is used that has the same KTPV as KTPV_max.

cset(expression, set)

The notation, cset(expression, set), is used to symbolically represent the containment set of an expression evaluated over a set of arguments. For example, for the expression, f(x, y) = xy, the containment constraint that the interval expression [0] × [+] must satisfy is

[0] × [+] cset(x × y, {(0,+)}) = [-, +].

degenerate interval

A degenerate interval is a zero-width interval. A degenerate interval is a singleton set, the only element of which is a point. In most cases, a degenerate interval can be thought of as a point. For example, the interval [2, 2] is degenerate, and the interval [2, 3] is not.

directed rounding

Directed rounding is rounding in a particular direction. In the context of interval arithmetic, rounding up is towards +, and rounding down is towards -. The direction of rounding is symbolized by the arrows, and . Therefore, with 5-digit arithmetic, 2.00001 = 2.0001. Directed rounding is used to implement interval arithmetic on computers so that the containment constraint is never violated.

disjoint interval

Two disjoint intervals have no elements in common. The intervals [2, 3] and [4, 5] are disjoint. The intersection of two disjoint intervals is the empty interval.

empty interval

The empty interval, [empty], is the interval with no members. The empty interval naturally occurs as the intersection of two disjoint intervals. For example, [2, 3]  [4,5] = [empty].

empty set

The empty set, , is the set with no members. The empty set naturally occurs as the intersection of two disjoint sets. For example, {2, 3} {4, 5} = .

ev(literal_constant)

The notation ev(literal_constant) is used to denote the external value defined by a literal constant character string. For example, ev(0.1) = 1/10, in spite of the fact that an internal approximation of 0.1 must be used, because the constant 0.1 is not machine representable.

exception

In the IEEE 754 floating-point standard, an exception occurs when an attempt is made to perform an undefined operation, such as division by zero.

exchangeable expression

Two expressions are exchangeable if they are containment-set equivalent (their containment sets are everywhere identical).

expression context

In widest-need expression processing, the two attributes that define expression context are the expression's type and the maximum KTPV (KTPV_max).

expression processing: strict

See strict expression processing.

expression processing: widest-need

See widest-need expression processing.

extended interval

The term extended interval refers to intervals whose endpoints can be extended real numbers, including - and +. For completeness, the empty interval is also included in the set of extended real intervals.

external representation

The external representation of a Fortran data item is the character string used to define it during input data conversion, or the character string used to display it after output data conversion.

external value

The external value of a Fortran literal constant is the mathematical value defined by the literal constant's character string. The external value of a literal constant is not necessarily the same as the constant's internal approximation, which, in the Fortran standard, is the only defined value of a literal constant. See ev(literal_constant).

hull

See interval hull.

infimum
(plural, infima)

The infimum of a set of numbers is the set's greatest lower bound. This is either the smallest number in the set or the largest number that is less than all the numbers in the set. The infimum, inf([a, b]), of the interval constant [a, b] is a.

interval algorithm

An interval algorithm is a sequence of operations used to compute an interval result.

internal approximation

In Fortran, the internal approximation of a literal constant is a machine representable value. There is no internal approximation accuracy requirement in the Fortran standard.

interval arithmetic

Interval arithmetic is the system of arithmetic used to compute with intervals.

interval box

An interval box is a parallelepiped with sides parallel to the n-dimensional Cartesian coordinate axes. An interval box is conveniently represented using an n-dimensional interval vector, X = (X₁, . . ., X_n)^T.

INTERVAL constant

An INTERVAL constant is the closed corrected set: [a, b] ={z | a z b} defined by the pair of numbers, a b.

INTERVAL constant's external value

An INTERVAL constant's external value is the mathematical value defined by the interval constant's character string. See also external value.

INTERVAL
constant's internal approximation

In f95, an INTERVAL constant's internal approximation is the sharp internal approximation of the constant's external value. Therefore, it is the narrowest possible machine representable interval that contains the constant's external value.

interval hull

The interval hull operator, , on a pair of intervals , is the smallest interval that contains both X and Y (also represented as ). For example,

[2, 3] [5, 6] = [2, 6].

INTERVAL-specific function

In f95, an INTERVAL-specific function is an interval function that is not an interval version of a standard Fortran function. For example, WID, MID, INF, and SUP, are INTERVAL-specific functions.

interval width

Interval width, w([a, b]) = b - a.

intrinsic INTERVAL
data type

In Fortran, there are four intrinsic numeric data types: INTEGER, REAL, DOUBLE PRECISION REAL, and COMPLEX. With the command line option -xia or -xinterval, f95 recognizes INTERVAL as an intrinsic data type.

intrinsic INTERVAL-specific function

In f95, there are a variety of intrinsic INTERVAL-specific functions, including: WID, HULL, MID, INF, and SUP.

kind type parameter value (KTPV)

In Fortran, each intrinsic data type is parameterized using a kind type parameter value (KTPV), which selects the kind (precision) of the data type. In f95, there are three INTERVAL KTPVs: 4, 8, and 16. The default interval KTPV is 8.

KTPV (kind type parameter value)

See kind type parameter value (KTPV).

KTPV_max

In widest-need expression processing of interval expressions, all intervals are converted to the maximum value of the KTPV of any data item in the expression. This maximum value is given the name KTPV_max.

left endpoint

The left endpoint of an interval is the same as its infimum or lower bound.

literal constant

In f95, an interval literal constant is the character string used to define the constant's external value.

literal constant's external value

In f95, an interval literal constant's external value is the mathematical value defined by the constant's character string. See also external value.

literal constant's internal approximation

In f95, an interval literal constant's internal approximation is the sharp machine representable interval that contains the constant's external value.

lower bound

See infimum (plural, infima).

mantissa

When written in scientific notation, a number consists of a mantissa or significand and an exponent power of 10. The E edit descriptor in Fortran displays numbers in terms of a mantissa or significand and an exponent, or power of 10.

mixed-KTPV INTERVAL expression

A mixed-KTPV INTERVAL expression contains constants and/or variables with different KTPVs. For example, [1_4] + [0.2_8] is a mixed-KTPV INTERVAL expression. Mixed-KTPV interval expressions are permitted under widest-need expression processing, but are not permitted under strict expression processing.

mixed-mode (type and KTPV) INTERVAL expression

A mixed-mode INTERVAL expression contains data items of different types and KTPV. For example, the expression [0.1] + 0.2 is a mixed-mode expression. [0.1] is an INTERVAL constant with KTPV = 8, while 0.2 is a REAL constant with KTPV = 4.

mixed-type INTERVAL expression

A mixed-type INTERVAL expression contains data items of different types. For example, the expression [0.1] + 0.2D0 is a mixed-type INTERVAL expression, because [0.1] is an INTERVAL, and 0.2D0 is a DOUBLE PRECISION constant. They both have the same KTPV = 8.

multiple-use expression (MUE)

A multiple-use expression (MUE) is an expression in which at least one independent variable appears more than once.

named constant

A named constant is declared and initialized in a PARAMETER statement. Because the value of a named constant is not context dependent, a more appropriate name for a data item in a PARAMETER declaration is "read-only variable."

narrow-width interval

Let the interval [a, b] be an approximation of the value . If w[a, b] = b - a, is small, [a, b] is a narrow-width interval. The narrower the width of the interval [a, b], the more accurately [a, b] approximates . See also sharp interval result.

opaque data type

An opaque data type leaves the structure of internal approximations unspecified. INTERVAL data items are opaque. Therefore, programmers cannot count on INTERVAL data items being internally represented in any particular way. The intrinsic functions INF and SUP provide access to the components of an interval. The INTERVAL constructor can be used to manually construct any valid interval.

point

A point (as opposed to an interval), is a number. A point in n-dimensional space, is represented using an n-dimensional vector, x = (x₁, . . . , x_n)^T. A point and a degenerate interval, or interval vector, can be thought of as the same. Strictly, any interval is a set, the elements of which are points.

possibly true relational operators

See relational operators: possibly true.

quality of implementation

Quality of implementation, is a phrase used to characterize properties of compiler support for intervals. Narrow width is a new quality of implementation opportunity provided by intrinsic compiler support for INTERVAL data types.

radix conversion

Radix conversion is the process of converting back and forth between external decimal numbers and internal binary numbers. Radix conversion takes place in formatted and list-directed input/output. Because the same numbers are not always representable in the binary and decimal number systems, guaranteeing containment requires directed rounding during radix conversion.

read-only variable

A read-only variable is not a defined construct in standard Fortran. Nevertheless, a read-only variable is a variable, the value of which cannot be changed once it is initialized. In standard Fortran, without interval support, there is no need to distinguish between a named constant and a read-only variable. Because widest-need expression processing uses the external value of constants, the distinction between a read-only variable and a named constant must be made. As implemented in f95, the symbolic name that is initialized in a PARAMETER declaration is a read-only variable.

relational operators: certainly true

The certainly true relational operators are {.CLT., .CLE., .CEQ., .CNE., .CGE., .CGT.}. Certainly true relational operators are true if the relation in question is true for all elements in the operand intervals. That is [a, b] .Cop. [c, d] = true if x .op. y = true for all .

For example, [a, b] .CLT. [c, d] if b < c.

relational operators: possibly true

The possibly true relational operators are {.PLT., .PLE., .PEQ., .PNE., .PGE., .PGT.}. Possibly true relational operators are true if the relation in question is true for any elements in operand intervals. For example, [a, b] .PLT. [c, d] if a < d.

relational operators: set

The set relational operators are {.SLT., .SLE., .SEQ., .SNE., .SGE., .SGT.}. Set relational operators are true if the relation in question is true for the endpoints of the intervals. For example, [a, b] .SEQ. [c, d] if (a = c) and (b = d).

right endpoint

See supremum (plural, suprema).

scope of widest-need expression processing

See widest-need expression processing: scope.

set theoretic

Set theoretic is the means of or pertaining to the algebra of sets.

sharp interval result

A sharp interval result has a width that is as narrow as possible. A sharp interval result is equal to the hull of an expression's containment. Given the limitations imposed by a particular finite precision arithmetic, a sharp interval result is the narrowest possible finite precision interval that contains the expression's containment set.

single-number
input/output

Single-number input/output, uses the single-number external representation for an interval, in which the interval [-1, +1]_uld is implicitly added to the last displayed digit. The subscript uld is an acronym for unit in the last digit. For example 0.12300 represents the interval 0.12300 + [-1, +1]_uld = [0.12299, 0.12301].

single-number INTERVAL data conversion

Single-number INTERVAL data conversion is used by the Y edit descriptor to read and display external intervals using the single-number representation. See single-number input/output.

single-use expression (SUE)

A single-use expression (SUE) is an expression in which each variable only occurs once. For example

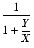
is a single use expression, whereas

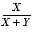
is not.

strict expression processing

Under strict expression processing, no automatic type or KTPV changes are made by the compiler. Mixed type and mixed KTPV INTERVAL expressions are not allowed. Any type and/or KTPV changes must be explicitly programmed.

supremum
(plural, suprema)

The supremum of a set of numbers is the set's least upper bound. This is either the largest number in the set or the smallest number that is greater than all the numbers in the set. The supremum, sup([a, b]), of the interval constant [a, b] is b.

unit in the last digit (uld)

In single number input/output, one unit in the last digit (uld) is added to and subtracted from the last displayed digit to implicitly construct an interval.

unit in the last place (ulp)

One unit in the last place (ulp) of an internal machine number is the smallest possible increment or decrement that can be made using the machine's arithmetic. Therefore, if the width of a computed interval is 1-ulp, this is the narrowest possible non-degenerate interval with a given KTPV.

upper bound

See supremum (plural, suprema).

valid interval result

A valid interval result, [a, b] must satisfy two requirements:

• a b
  
• [a, b] must not violate the containment constraint

value assignment

In Fortran, an assignment statement computes the value of the expression to the right of the assignment of value operator, =, and stores the value in the variable, array element, or array to the left of the assignment of value operator.

widest-need expression processing

Under widest-need expression processing, automatic type and KTPV changes are made by the compiler. Any non-interval subexpressions are promoted to intervals and KTPVs are set to KTPV_max.

widest-need expression processing: scope

In Fortran, scope refers to that part of an executable program where data and/or operations are defined and unambiguous. The scope of widest-need expression processing is limited by calls to functions and subroutines.