| Interval Arithmetic Programming Reference |
f95Interval ReferenceThis chapter is a reference for the syntax and semantics of the intrinsic
INTERVALtypes implemented in Sun WorkShop 6 Fortran 95. The sections can be read in any order.Unless explicitly stated otherwise, the
INTERVALdata type has the same properties as other intrinsic numeric types. This chapter highlights differences between theREALandINTERVALtypes.Some code examples are not complete programs. The implicit assumption is that these examples are compiled with the -
xiacommand line option.2.1 Fortran Extensions
INTERVALdata types are a non-standard extension to Fortran. However, where possible, the implemented syntax and semantics conform to the style of Fortran.2.1.1 Character Set Notation
Left and right square brackets, "
[...]", are added to the Fortran character set to delimit literalINTERVALconstants.Throughout this document, unless explicitly stated otherwise,
INTEGER,REAL, andINTERVALconstants mean literal constants. Constant expressions and named constants (PARAMETERS) are always explicitly identified as such.TABLE 2-1 shows the character set notation used for code and mathematics.
Note – Pay close attention to font usage. Different fonts represent an interval's exact, external mathematical value and an interval's machine-representable, internal approximation.
2.1.2
INTERVALConstantsIn
f95, anINTERVALconstant is either a single integer or real decimal number enclosed in square brackets,[3.5], or a pair of integer or real decimal numbers separated by a comma and enclosed in square brackets,[3.5E-10,3.6E-10]. If a degenerate interval is not machine representable, directed rounding is used to round the exact mathematical value to an internal machine representable interval known to satisfy the containment constraint.An
INTERVALconstant with both endpoints of type defaultINTEGER, defaultREALorREAL(8), has the default typeINTERVAL.If an endpoint is of type default
INTEGER, defaultREALorREAL(8), it is internally converted to a value of the typeREAL(8).If an endpoint's type is
INTEGER(8), it is internally converted to a value of typeREAL(16).If an endpoint's type is
INTEGER(4), it is internally converted to a value of typeREAL(8).If an endpoint's type is
INTEGER(1)orINTEGER(2), it is internally converted to a value of typeREAL(4).If both endpoints are of type
REALbut have different KTPVs, they are both internally represented using the approximation method of the endpoint with greater decimal precision.The KTPV of an
INTERVALconstant is the KTPV of the part with the greatest decimal precision.CODE EXAMPLE 2-1 shows the KTPV of various
CODE EXAMPLE 2-1 KTPV ofINTERVALconstants.INTERVALConstants
A Fortran constant, such as
0.1or[0.1,0.2], is associated with the two values: the external value it represents and its internal approximation. In Fortran, the value of a constant is its internal approximation. There is no need to distinguish between a constant's external value and its internal approximation. Intervals require this distinction to be made. To represent a Fortran constant's external value, the following notation is used:
- ev(
0.1) = 0.1 or ev([0.1,0.2])= [0.1, 0.2].The notation ev stands for external value.
Following the Fortran Standard, the numerical value of an
INTERVALconstant is its internal approximation. The external value of anINTERVALconstant is always explicitly labelled as such.For example, the
INTERVALconstant[1,2]and its external value ev([1,2]) are equal to the mathematical value [1, 2]. However, while ev([0.1,0.2]) = [0.1, 0.2],[0.1,0.2]is only an internal machine approximation, because the numbers 0.1 and 0.2 are not machine representable. The value of theINTERVALconstant,[0.1,0.2]is its internal machine approximation. The external value is denoted ev([0.1,0.2]).Under strict expression processing, an
INTERVALconstant's internal approximation is fixed, as it is for other Fortran numeric typed constants. The value of aREALconstant is its internal approximation. Similarly, the value of anINTERVALconstant's internal approximation is referred to as the constant's value. A constant's external value, which is not a defined concept in standard Fortran, can be different from its internal approximation. Under widest-need expression processing, anINTERVALconstant's internal value is context-dependent. Nevertheless, anINTERVALconstant's internal approximation must contain its external value in bothstrictand widest-need expression processing.Like any mathematical constant, the external value of an
INTERVALconstant is invariant. The external value of a namedINTERVALconstant (PARAMETER) cannot change within a program unit. However, as with any named constant, in different program units, different values can be associated with the same named constant.Because intervals are opaque, there is no language requirement to store the information needed to internally represent an interval. Intrinsic functions are provided to access the infimum and supremum of an interval. Nevertheless, an
INTERVALconstant is defined by an ordered pair ofREALorINTEGERconstants. The constants are separated by a comma, and the pair is enclosed in square brackets. The first constant is the infimum or lower bound, and the second, is the supremum or upper bound.If only one constant appears inside the square brackets, the represented interval is degenerate, having equal infimum and supremum. In this case, an internal interval approximation is constructed that is guaranteed to contain the single decimal literal constant's external value.
A valid interval must have an infimum that is less than or equal to its supremum. Similarly, an
INTERVALconstant must also have an infimum that is less than or equal to its supremum. For example, the following code fragment must evaluate to true:
INF([0.1]).LE. SUP([0.1]).CODE EXAMPLE 2-2 contains examples of valid and invalid
INTERVALconstants.For additional information regarding
CODE EXAMPLE 2-2 Valid and InvalidINTERVALconstants, see the supplementary paper [4] cited in Section 2.10 References.INTERVALConstants
2.1.3 Internal Approximation
The internal approximation of a
REALconstant does not necessarily equal the constant's external value. For example, because the decimal number 0.1 is not a member of the set of binary floating-point numbers, this value can only be approximated by a binary floating-point number that is close to 0.1. ForREALdata items, the approximation accuracy is unspecified in the Fortran standard. ForINTERVALdata items, a pair of floating-point values is used that is known to contain the set of mathematical values defined by the decimal numbers used to symbolically represent anINTERVALconstant. For example, the mathematical interval [0.1, 0.2] is the external value of theINTERVALconstant[0.1,0.2].Just as there is no Fortran language requirement to accurately approximate
REALconstants, there is also no language requirement to approximate an interval's external value with a narrow widthINTERVALconstant. There is a requirement for anINTERVALconstant to contain its external value.
- ev(
INF([0.1,0.2]))inf(ev(
[0.1,0.2])) = inf([0.1, 0.2])
- sup([0.1, 0.2]) = sup(ev(
[0.1,0.2]))ev(
SUP([0.1,0.2]))
f95INTERVALconstants are sharp. This is a quality of implementation feature.2.1.4
INTERVALStatementThe
INTERVALdeclaration statement is the onlyINTERVAL-specific statement added to the Fortran language inf95. For a detailed description of theINTERVALdeclaration statement and standard Fortran statements that interact withINTERVALdata items, see INTERVAL Statements.2.2 Data Type and Data Items
If the
-xiaor-xintervaloptions are entered in thef95command line, or if they are set either towidestneedor tostrict, theINTERVALdata type is recognized as an intrinsic numeric data type inf95. If neither option is entered in thef95command line, or if they are set tono,theINTERVALdata type is not recognized as intrinsic. See Section 2.3.3 Interval Command-Line Options for details on theINTERVALcommand-line options.2.2.1 Name:
INTERVALThe intrinsic type
INTERVALis added to the six intrinsic Fortran data types. TheINTERVALtype is opaque, meaning that anINTERVALdata item's internal format is not specified. Nevertheless, anINTERVALdata item's external format is a pair ofREALdata items having the same kind type parameter value (KTPV) as theINTERVALdata item.2.2.2 Kind Type Parameter Value (KTPV)
An
INTERVALdata item is an approximation of a mathematical interval consisting of a lower bound or infimum and an upper bound or supremum.INTERVALdata items have all the properties of other numeric data items.The KTPV of a default
INTERVALdata item is 8. The size of a defaultINTERVALdata item with no specified KTPV is 16 bytes. The size of a defaultINTERVALdata item inf95cannot be changed using the-xtypemapor-r8constcommand line options. For more information, see Section 2.3.3.1 -xtypemap and -r8const Command-Line Options. Thus
KIND([0])=2*KIND(0)=KIND(0.0_8)=8provided the size of the default
REALandINTEGERdata items is not changed using-xtypemap.2.2.2.1 Size and Alignment Summary
The size and alignment of
INTERVALtypes is unaffected byf95compiler options. TABLE 2-2 containsINTERVALsizes and alignments.
TABLE 2-2 INTERVALSizes and Alignments
Note –INTERVALarrays align the same as their elements.
2.2.3
INTERVALArrays
INTERVALarrays have all the properties of arrays with different numeric types. See CODE EXAMPLE 2-25 for the declaration ofINTERVALarrays.Interval versions of the following intrinsic array functions are supported:
ALLOCATED(),ASSOCIATED(),CSHIFT(),DOT_PRODUCT(),EOSHIFT(),KIND(),LBOUND(),MATMUL(),MAXVAL(),MERGE(),MINVAL(),NULL(),PACK(),PRODUCT(),RESHAPE(),SHAPE(),SIZE(),SPREAD(),SUM(),TRANSPOSE(),UBOUND(),UNPACK().The
MINLOC(), andMAXLOC()intrinsic functions are not defined forINTERVALarrays because theMINVALandMAXVALintrinsic applied to anINTERVALarray may return an interval value not possessed by any element of the array. See the following sections for descriptions of theMAXandMINintrinsic functionsFor example
MINVAL((/[1,2],[3,4]/))=[1,3]and
MAXVAL(/[1,2],[3,4]/) = [2,4].Array versions of the following intrinsic
INTERVAL-specific functions are supported:ABS(),INF(),INT(),MAG(),MAX(),MID(),MIG(),MIN(),NDIGITS(),SUP(),WID().Array versions of the following intrinsic
INTERVAL-mathematical functions are supported:ACOS(),AINT(),ANINT(),ASIN(),ATAN(),ATAN2(),CEILING(),COS(),COSH(),EXP(),FLOOR(),LOG(),LOG10(),MOD(),SIGN(),SIN(),SINH(),SQRT(),TAN(),TANH().Array versions of the following
INTERVALconstructors are supported:INTERVAL(),DINTERVAL(),SINTERVAL(),QINTERVAL().2.3
INTERVALArithmetic Expressions
INTERVALarithmetic expressions are constructed from the same arithmetic operators as other numerical data types. The fundamental difference betweenINTERVALand non-INTERVAL(point) expressions is that the result of any possibleINTERVALexpression is a validINTERVALthat satisfies the containment constraint of interval arithmetic. In contrast, point expression results can be any approximate value.2.3.1 Mixed-Mode
INTERVALExpressionsMixed-mode (
INTERVAL-point) expressions require widest-need expression processing to guarantee containment. Expression processing is widest-need by default when support for intervals is invoked using either the-xiacommand-line macro or the-xintervalcommand line option. If widest-need expression processing is not wanted, use the options-xia=strictor-xinterval=strictto invoke strict expression processing. Mixed-modeINTERVALexpressions are compile-time errors under strict expression processing. Mixed-mode operations betweenINTERVALandCOMPLEXoperands are not supported.With widest-need expression processing, the KTPV of all operands in an interval expression is promoted to KTPVmax, the highest
INTERVALKTPV found anywhere in the expression.
Note – KTPV promotion is performed before expression evaluation.
Widest-need expression processing guarantees:
- Interval containment
- No type or precision conversions add width to the converted intervals.
Caution – Unless there is a specific requirement to use strict expression processing, it is strongly recommended that users employ widest-need expression processing. In any expression or subexpression, explicitINTERVALtype and KTPV conversions can always be made.
Each of the following examples is designed to illustrate the behavior and utility of widest-need expression processing. There are three blocks of code in each example:
- Generic code that is independent of the expression processing mode (widest-need, or strict)
- Widest-need code
- Equivalent strict code
The examples are designed to communicate three messages:
- Except in special circumstances, use the widest-need expression processing.
- Whenever widest-need expression processing is enabled, but is not wanted, it can be overridden using the
INTERVALconstructor to coerce type and KTPV conversions.- With strict expression processing,
INTERVALtype and precision conversions must be explicitly specified usingINTERVALconstants and theINTERVALconstructor.2.3.2 Value Assignment
The
INTERVALassignment statement assigns a value of anINTERVALscalar, array element, or array expression to anINTERVALvariable, array element or array. The syntax is:
V =exprwhere
expris a placeholder for an interval arithmetic or array expression, andVis anINTERVALvariable, array element, or array.Executing an
INTERVALassignment causes the expression to be evaluated using either widest-need or strict expression processing. The resulting value is then assigned toV. The following steps occur when evaluating an expression using widest-need expression processing:CODE EXAMPLE 2-3 KTPVmax Depends on
- The interval KTPV of every point (non-
INTERVAL) data item is computed.- The expression, including the left-hand side of an assignment statement, is scanned for the maximum interval KTPV, denoted KTPVmax.
- All point and
INTERVALdata items in theINTERVALexpression are promoted to KTPVmax, prior to evaluating the expression.- If
KIND(V)< KTPVmax, the expression result is converted to a containing interval with KTPV =KIND(V)and the resulting value is assigned toV.KIND(Left-Hand Side)
Note – Under widest-need, the KTPV of the variable to which assignment is made (the left-hand side) is included in determining the value of KTPVmax to which all items in anINTERVALstatement are promoted.
CODE EXAMPLE 2-4 Mixed-Mode Assignment Statement
CODE EXAMPLE 2-4 notes:
- The equivalent strict code shows the steps required to reproduce the results obtained using widest-need expression processing.
- In line 4,
KIND(R)= 8, butKIND(X1)= 4. To guarantee containment and produce a sharp result,Ris converted to a KTPVmax = 8 containing interval before evaluating the expression. Then the result is converted to a KTPV-4 containing interval and assigned toX1. These steps are made explicit in the equivalent strict code in line 6.- In line 5,
KIND(R)=KIND(X2)= 8. Therefore,X1is promoted to a KTPV-8INTERVALbefore the expression is evaluated and the result assigned toX2. Line 7 shows the equivalent strict code.- The checks in lines 8 and 9 verify that the widest-need and strict results are identical. For more detailed information on widest-need and strict expression processing, see Section 2.3 INTERVAL Arithmetic Expressions.
2.3.3 Interval Command-Line Options
Interval features in the
f95compiler are activated by means of the following command-line options:
-xinterval=(no|widestneed|strict)is a command-line option to enable processing of intervals and to control permitted expression evaluation syntax.
- "
no" disables the interval extensions tof95.- "
widestneed" enables widest-need expression processing and functions the same as-xintervalif no option is specified. See Section 2.3.1 Mixed-Mode INTERVAL Expressions.- "
strict" requires allINTERVALtype and KTPV conversions to be explicit, or it is a compile-time error, as described in Section 1.5 Error Detection.-xia=(widestneed|strict)is a macro that enables the processing ofINTERVALdata types and sets a suitable floating-point environment. If-xiais not mentioned (the first default), there is no expansion.
-xiaexpands into:
-xinterval=widestneed-ftrap=%none-fns=no-fsimple=0-xia=(widestneed|strict)expands into:
-xinterval=(widestneed|strict)
-ftrap=%none
-fns=no
-fsimple=0- Previously set values of
-ftrap,-fns,-fsimpleare superseded.It is a fatal error if at the end of command line processing
xinterval=(widestneed|strict)is set, and either-fsimpleor-fnsis set to any value other than-fsimple=0-fns=noWhen using command-line options:
- At the end of the command-line processing, if
-ansiis set and-xintervalis set to eitherwidestneedorstrict, the following warning is issued:"Interval data types are a non-standard feature".-fround = <r>: (Set the IEEE rounding mode in effect at startup) does not interact with-xiabecauseINTERVALoperations and routines save and restore the rounding mode upon entry and exit.When recognition of
INTERVALtypes is activated:
INTERVALoperators and functions become intrinsic.- The same restrictions are imposed on the extension of intrinsic
INTERVALoperators and functions as are imposed on the extension of standard intrinsic operators and functions.- Intrinsic
INTERVAL-specific function names are recognized. See Section 2.2.3 INTERVAL Arrays and Section 2.9.4 Mathematical Functions.2.3.3.1
-xtypemapand-r8constCommand-Line OptionsThe size of a default
INTERVALvariable declared only with theINTERVALkeyword cannot be changed using the-xtypemapand-r8constcommand line options.While these command line options have no influence on the size of default
INTERVALtypes, the options can change the result of mixed-modeINTERVALexpressions, as shown in CODE EXAMPLE 2-5.
Note – Although-xtypemaphas no influence on the KTPV ofX, it can influence the value ofX.
2.3.4 Constant Expressions
CODE EXAMPLE 2-6 Constant Expressions
INTERVALconstant expressions may containINTERVALliteral and named constants, as well as any point constant expression components. Therefore, each operand or argument is itself, another constant expression, a constant, a named constant, or an intrinsic function called with constant arguments.
cat ce2-6.f95INTERVAL :: P, Q! Widest-need codeP = SIN([1.23])+[3.45]/[9, 11.12]! Equivalent strict codeQ = SIN([1.23_8])+[3.45_8]/[9.0_8, 11.12_8]IF(P .SEQ. Q) PRINT *, 'Check'ENDmath%f95 -xia ce2-6.f95math%a.outCheck
Note – Under widest-need expression processing, interval context is used to determine the KTPV ofINTERVALconstants. See Section 1.3.7 Default Kind Type Parameter Value (KTPV) for more information.
INTERVALconstant expressions are permitted wherever anINTERVALconstant is allowed.2.4 Intrinsic Operators
TABLE 2-3 lists the intrinsic operators that can be used with intervals. In TABLE 2-3,
XandYare intervals.
TABLE 2-3 INTRINSICOperators**Exponentiation X**YRaise Xto theINTERVALpowerYX**NRaise Xto theINTEGERpowerN(See Note 1)*Multiplication X*YMultiply XandY/Division X/YDivide XbyY+Addition X+YAdd XandY+Identity +XSame as X(without a sign)-Subtraction X-YSubtract YfromX-Numeric Negation -XNegate X.IH.INTERVALhullX.IH.YInterval hull of XandY.IX.Intersection X.IX.YIntersect XandY1. If N is an integer expression, overflow can cause a containment failure. Users must be responsible for preventing integer overflow in this release. See Section 1.5.1.1 Integer Overflow for more information.
- The operator ** takes precedence over the *, /, +, -,
.IH., and.IX.operators.- The operators * and / take precedence over the +, -,
.IH., and.IX.operators.- The operators + and - take precedence over the
.IH.and.IX.operators.- The operators .
IH. and .IX. take precedence over the // operator.With the exception of the interval ** operator and an integer exponent, interval operators can only be applied to two interval operands with the same kind type parameter value. Thus the type and KTPV of an interval operator's result are the same as the type and KTPV of its operands.
If the second operand of the interval ** operator is an integer, the first operand can be of any interval KTPV. In this case, the result has the type and KTPV of the first operand.
Some
INTERVAL-specific operators have no point analogs. These can be grouped into three categories: set, certainly, and possibly, as shown in TABLE 2-4. A number of unique set-operators have no certainly or possibly analogs.
TABLE 2-4 Intrinsic INTERVALRelational OperatorsSet Relational Operators . EQ.
(same as ==). NEQ.
(same as /=)Certainly Relational Operators Possibly Relational Operators
The precedence of intrinsic
INTERVALrelational operators is the same as the precedence ofREALrelational operators.Except for the .
IN. operator, intrinsicINTERVALrelational operators can only be applied to twoINTERVALoperands with the same KTPV.The first operand of the .
IN. operator is of anyINTEGERorREALtype. The second operand can have any interval KTPV.The result of the
INTERVALrelational expression has the defaultLOGICALkind type parameter.2.4.1 Arithmetic Operators
+,-,*,/Formulas for computing the endpoints of interval arithmetic operations on finite
REALintervals are motivated by the requirement to produce the narrowest interval that is guaranteed to contain the set of all possible point results. Ramon Moore independently developed these formulas and more importantly, was the first to develop the analysis needed to apply interval arithmetic. For more information, see R. Moore, Interval Analysis, Prentice-Hall, 1966.The set of all possible values was originally defined by performing the operation in question on any element of the operand intervals. Therefore, given finite intervals, [a, b] and [c, d], with
,
,
with division by zero being excluded. The formulas, or their logical equivalent, are:
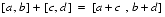
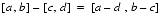
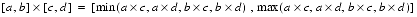
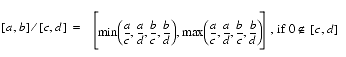
Directed rounding is used when computing with finite precision arithmetic to guarantee the set of all possible values is contained in the resulting interval.
The set of values that any interval result must contain is called the containment set of the operation or expression that produces the result.
To include extended intervals (with infinite endpoints) and division by zero, containment sets cannot directly depend on the value of arithmetic operations on real values. For extended intervals, containment sets are required for operations on points that are normally undefined. Undefined operations include the indeterminate forms
.
The containment-set closure identity solves the problem of identifying the value of containment sets of expressions at singular or indeterminate points. The identity states that containment sets are closures. The closure of a function at a point on the boundary of its domain includes all limit or accumulation points. For details, see the Glossary and the supplementary papers [1], [3], [10], and [11] cited in Section 2.10 References.
Symbolically, cset(x op y, {(x0, y0)}) =
, where
denotes the closure of the operation, op, and {x0} denotes the singleton set with only one element, x0. The subscript 0 is used to symbolically distinguish a particular value, x0, of the variable, x, from the variable itself. For example, with x0 = 1, op = ÷, and y0 = 0, x0³ ÷ y0 is undefined, but the closure,
.
This result is obtained using the sequences
or
,

Using the two sequences, {yj}, above, the closure of the division operator at x0 = 1 and y0 = 0 is:
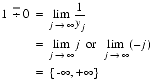
The following tables, TABLE 2-5 through TABLE 2-9, display containment sets for the four basic arithmetic operations.
TABLE 2-5 Containment Set for Addition: cset(x +y, {(x0, y0)}) {- }
{- }
{- }
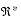
{real: x0} {- }
{x0 + y0} {+ }
{+ }
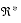
{+ }
{+ }
TABLE 2-6 Containment Set for Subtraction: cset(x - y, {(x0, y0)}) {- }
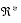
{- }
{- }
{real: x0} {+ }
{x0 - y0} {- }
{+ }
{+ }
{+ }
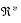
TABLE 2-7 Containment Set for Multiplication: cset(x × y, {(x0, y0)}) {- }
{+ }
{+ }
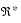
{- }
{- }
{real: x0 < 0} {+ }
{x × y} {0} {x × y} {- }
{0} 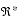
{0} {0} {0} 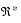
{real: x0 > 0} {- }
x × y {0} x × y {+ }
{+ }
{- }
{- }
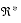
{+ }
{+ }
TABLE 2-8 Containment Set for Division: cset(x ÷ y, {(x0, y0)}) {- }
[0, + ]
{+ }
{- , +
}
{- }
[- , 0]
{real: x0 0}
{0} {x ÷ y} {- , +
}
{x ÷ y} {0} {0} {0} {0} 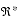
{0} {0} {+ }
[- , 0]
{- }
{- , +
}
{+ }
[0, + ]
All inputs in the tables are shown as singletons. Results are shown as singletons, sets, or intervals. To avoid ambiguity, customary notation, such as
,
, and
, is not used. These tables show the results for singleton-set inputs to each operation. Results for general set (or interval) inputs are the union of the results of the single-point results as they range over the input sets (or intervals).
In one case, division by zero, the result is not an interval, but the set,
. In this case, the narrowest interval in the current system that does not violate the containment constraint of interval arithmetic is the interval
.
Sign changes produce the expected results.
To incorporate these results into the formulas for computing interval endpoints, it is only necessary to identify the desired endpoint, which is also encoded in the rounding direction. Using
to denote rounding down (towards -
) and
to denote rounding up (towards +
),
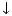
and
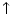
.
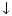
and
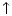
.
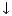
and
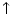
.
Finally, the empty interval is represented in Fortran by the character string
[empty]and has the same properties as the empty set, denotedin the algebra of sets. Any arithmetic operation on an empty interval produces an empty interval result. For additional information regarding the use of empty intervals, see the supplementary papers [6] and [7] cited in Section 2.10 References.
Using these results,
f95implements the closed interval system. The system is closed because all arithmetic operations and functions always produce valid interval results. See the supplementary papers [2] and [8] cited in Section 2.10 References.2.5 Power Operators
X**NandX**YThe power operator can be used with integer exponents (
X**N) and continuous exponents (X**Y). With a continuous exponent, the power operator has indeterminate forms, similar to the four arithmetic operators.In the integer exponents case, the set of all values that an enclosure of
must contain is
.
Monotonicity can be used to construct a sharp interval enclosure of the integer power function. When n = 0, cset(xn, {x0})= 1 for all
, and
[empty]**N=[empty]for allN.In the continuous exponents case, the set of all values that an interval enclosure of
must contain is

where
is the containment set of the expression
. The function exp(y ln (x)) makes explicit that only values of
need be considered, and is consistent with the definition of
X**YwithREALarguments in Fortran.The result is empty if either
INTERVALargument is empty, or if x < 0. This is also consistent with the point version ofX**Yin Fortran.TABLE 2-9 displays the containment sets for all the singularities and indeterminate forms of cset(exp(yln(x)), {(y0, x0)}).
TABLE 2-9 cset(exp(yln(x)), {(y0, x0)}) 0 y0 < 0 + 1 - [0,+ ]
1 + [0,+ ]
+ 0 [0,+ ]
0 0 [0,+ ]
The results in TABLE 2-9 can be obtained in two ways:
- Directly computing the closure of the composite expression, exp(yln(x)) for the values of x0 and y0 for which the expression is undefined.
- Use the containment-set evaluation theorem to bound the set of values in a containment set.
For most compositions, the second option is much easier. If sufficient conditions are satisfied, the closure of a composition can be computed from the composition of its closures. That is, the closure of each sub-expression can be used to compute the closure of the entire expression. In the present case,
- cset(exp(yln(x)), {x0, y0}) =
.
- cset(exp(yln(x)), {x0, y0})

.
Note that this is exactly how interval arithmetic works on intervals. The needed closures of the ln and exp functions are:
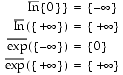
A necessary condition for closure-composition equality is that the expression must be a single-use expression (or SUE), which means that each independent variable can appear only once in the expression.
In the present case, the expression is clearly a SUE.
The entries in TABLE 2-9 follow directly from using the containment set of the basic multiply operation in TABLE 2-7 on the closures of the ln and exp functions. For example, with x0 = 1 and y0 = -
, ln(x0) = 0. For the closure of multiplication on the values -
and 0 in TABLE 2-7, the result is [-
, +
]. Finally, exp([-
, +
]) = [0, +
], the second entry in TABLE 2-9. Remaining entries are obtained using the same steps. These same results are obtained from the direct derivation of the containment set of exp(yln(x)). At this time, sufficient conditions for closure-composition equality of any expression have not been identified. Nevertheless,
- The containment-set evaluation theorem guarantees that a containment failure can never result from computing a composition of closures instead of a closure.
- An expression must be a SUE for closure-composition equality to be true.
2.6 Set Theoretic Operators
f95supports the following set theoretic operators for determining the interval hull and intersection of two intervals.2.6.1 Hull: X U Y or
(X.IH.Y)Description: Interval hull of two intervals. The interval hull is the smallest interval that contains all the elements of the operand intervals.
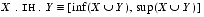

Arguments:
XandYmust be intervals with the same KTPV.2.6.2 Intersection: X
Y or
(X.IX.Y)Description: Intersection of two intervals.
Mathematical and operational definitions:
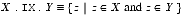
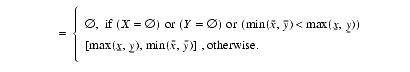
Arguments:
XandYmust be intervals with the same KTPV.2.7 Set Relations
f95 provides the following set relations that have been extended to support intervals.
2.7.1 Disjoint: X
Y =
or
(X.DJ.Y)Description: Test if two intervals are disjoint.
Mathematical and operational definitions:
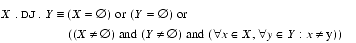
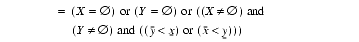
Arguments: X and
Ymust be intervals with the same KTPV.Result type: Default logical scalar.
2.7.2 Element: r
Y or
(R.IN.Y)Description: Test if the number,
R, is an element of the interval,Y.Mathematical and operational definitions:
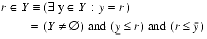
Arguments: The type of
RisINTEGERorREAL,and the type ofYisINTERVAL.Result type: Default logical scalar.
The following comments refer to the
set relation:
- Under widest-need expression processing,
RandYhaving different KTPVs has no impact on how they are evaluated. Widest-need expression processing applies toY, but does not apply to the evaluation ofR. After evaluation, KTPV promotion ofYorRis done before the inclusion test is performed.- Under strict expression evaluation,
RandYmust have the same KTPV.- If
RisNaN(Not a Number),R.IN.Yis unconditionally false.- If
Yis empty,R.IN.Yis unconditionally false.2.7.3 Interior:
(X.INT.Y)Description: Test if
Xis in interior ofY.The interior of a set in topological space is the union of all open subsets of the set.
For intervals, the relation
X.INT.Y(X in interior of Y) means that X is a subset of Y, and both of the following relations are false:
, or in Fortran:
INF(Y).IN.X, or in Fortran:
SUP(Y).IN.XNote also that,
, but
[empty].INT.[empty]= trueThe empty set is open and therefore is a subset of the interior of itself.
Mathematical and operational definitions:
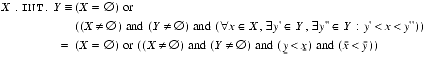
Arguments:
XandYmust be intervals with the same KTPV.Result type: Default logical scalar.
2.7.4 Proper Subset: X
Y or
(X.PSB.Y)Description: Test if
Xis a proper subset ofYMathematical and operational definitions:

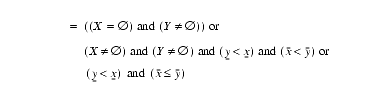
Arguments:
XandYmust be intervals with the same KTPV.Result type: Default logical scalar.
2.7.5 Proper Superset: X
Y or
(X.PSP.Y)Description: See proper subset with
.
2.7.6 Subset: X
Y or
(X.SB.Y)Description: Test if
Xis a subset ofYMathematical and operational definitions:
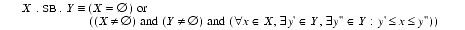
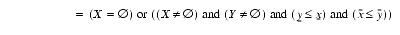
Arguments:
XandYmust be intervals with the same KTPV.Result type: Default logical scalar.
2.7.7 Superset: X
Y or
(X.SP.Y)Description: See subset with
.
2.7.8 Relational Operators
An intrinsic
INTERVALrelational operator, denoted.qop., is composed by concatenating:
- The required period delimiters
- An operator prefix,
q{
C,P,S}, whereC,P, andSstand for certainly, possibly, and set, respectively- A Fortran relational operator suffix,
op{
LT,LE,EQ,NE,GT,GE}In place of
.SEQ.and.SNE.,.EQ.(or==) and.NE.(or/=) defaults are accepted. To eliminate code ambiguity, all otherINTERVALrelational operators must be made explicit by specifying a prefix.All
INTERVALrelational operators have equal precedence. Arithmetic operators have higher precedence than relational operators.
INTERVALrelational expressions are evaluated by first evaluating the two operands, after which the two expression values are compared. If the specified relationship holds, the result value is true; otherwise, it is false.When widest-need expression processing is invoked, it applies to both
INTERVALoperand expressions ofINTERVALrelational operators.Letting "nop" stand for the complement of the operator op, the certainly and possibly operators are related as follows:
.Cop.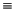
.NOT.(.Pnop.).Pop.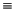
.NOT.(.Cnop.)
Caution – This identity between certainly and possibly operators holds unconditionally ifop{
EQ,NE}, and otherwise, only if neither operand is empty. Conversely, the identity does not hold ifop{
LT,LE,GT,GE} and either operand is empty.
Assuming neither operand is empty, TABLE 2-10 contains the Fortran operational definitions of all
INTERVALrelational operators of the form:
[x,x].qop.[y,y].The first column contains the value of the prefix, and the first row contains the value of the operator suffix. If the tabled condition holds, the result is true.
TABLE 2-10 Operational Definitions of Interval Order Relations
.Sx <y andx < yx y andxyx =y andx = yx yandxyx >yandx > yx y orxy
.C
x <y
xyyx and
xy
xy
x> yx > yor y> x
.P
x< y
xyx yand yx
xy
x >yy >x orx >y
CODE EXAMPLE 2-7 Relational Operators
cat ce2-7.f95INTERVAL :: X = [1.0, 3.0], Y = [2.0, 4.0], ZINTEGER :: V = 4, W = 5LOGICAL :: L1, L2, L3, L4REAL :: RL1 = (X == X) .AND. (Y .SEQ. Y)L2 = X .SLT. Y! Widest-need codeZ = WL3 = W .CEQ. ZL4 = X-Y .PLT. V-WIF( L1 .AND. L2 .AND. L3 .AND. L4) PRINT *, 'Check1'! Equivalent (for the assignment to L3 and L4) strict codeL3 = INTERVAL(W, KIND=8) .CEQ. ZL4 = X-Y .PLT. INTERVAL(V, KIND=8)-INTERVAL(W, KIND=8)IF(L3 .AND. L4) PRINT *, 'Check2'ENDmath%f95 -xia ce2-7.f95math%a.outCheck1Check2CODE EXAMPLE 2-7 notes:
L1is true because an interval is set-equal to itself and the default.EQ.( or == ) operator is the same as.SEQ..L2is true because(INF(X).LT.INF(Y)).AND.(SUP(X).LT.SUP(Y))is true.L3is true because widest need promotesWto the interval[5,5]and two intervals are certainly equal if and only if all four of their endpoints are equal.L4is true because evaluating the interval expressionsX-YandV-Wyields the intervals[-3,1]and[-1,-1]respectively. Therefore the expression (INF(X-Y).LT.SUP(V-W))is true.2.7.8.1 Set Relational Operators
For an affirmative order relation with
op{
LT,LE,EQ,GE,GT} and,
between two points
, the mathematical definition of the corresponding set-relation, .
Sop., between two non-empty intervalsis:
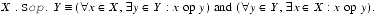
For the relation
between two points
, the corresponding set relation,
.SNE., between two non-empty intervals X and Y is:
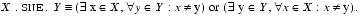
Empty intervals are explicitly considered in each of the following relations. In each case:
Arguments:
XandYmust be intervals with the same KTPV.Result type: default logical scalar.
2.7.8.2 Certainly Relational Operators
The certainly relational operators are true if the underlying relation is true for every element of the operand intervals. For example,
[a,b].CLT.[c,d]is true if x < y for alland
. This is equivalent to b < c.
For an affirmative order relation with
op{
LT,LE,EQ,GE,GT} and,
between two points x and y, the corresponding certainly-true relation .
Cop. between two intervals,XandY, is
.
With the exception of the anti-affirmative certainly-not-equal relation, if either operand of a certainly relation is empty, the result is false. The one exception is the certainly-not-equal relation,
.CNE., which is true in this case.For each of the certainly relational operators:
Arguments:
XandYmust be intervals with the same KTPV.Result type: default logical scalar.
2.7.8.3 Possibly Relational Operators
The possibly relational operators are true if any element of the operand intervals satisfy the underlying relation. For example,
[a,b].PLT.[c,d]is true if there exists anand a
such that x < y. This is equivalent to a < d.
For an affirmative order relation with
op{
LT,LE,EQ,GE,GT} and,
between two points x and y, the corresponding possibly-true relation .Pop. between two intervals X and Y is defined as follows:
.
If the empty interval is an operand of a possibly relation then the result is false. The one exception is the anti-affirmative possibly-not-equal relation,
.PNE., which is true in this case.For each of the possibly relational operators:
Arguments:
XandYmust beINTERVALSwith the same KTPV.Result type: default logical scalar.
2.8 Extending Intrinsic
INTERVALOperatorsIf the operator specified in the
INTERFACEstatement of a user provided operator interface block is an intrinsicINTERVALoperator (for example.IH.), an extension to the intrinsicINTERVALoperator is created.A user-provided operator function that extends an intrinsic
INTERVALoperator may not extend the operator for those data types of its operands for which this operator is predefined.For the combinations of arguments listed below, intrinsic interval operators +, -, *, /, .
IH., .IX., and ** are predefined and cannot be extended by users.
- (any
INTERVALtype, anyINTERVALtype)- (any
INTERVALtype, anyREALorINTEGERtype)- (any
REALorINTEGERtype, anyINTERVALtype)The interval operator ** with the integer exponent is predefined and cannot be extended by users for the following combination of arguments:
- (any
INTERVALtype, anyINTEGERtype)Except for the operator .
IN. interval relational operators are predefined for the combinations of arguments listed below and cannot be extended by users.
- (any
INTERVALtype, anyINTERVALtype)- (any
INTERVALtype, anyREALorINTEGERtype)- (any
REALorINTEGERtype, anyINTERVALtype)The interval relational operator .
IN. is predefined and cannot be extended by users for the following combination of arguments:
- (any
REALorINTEGERtype, anyINTERVALtype)In CODE EXAMPLE 2-8, both
S1andS2interfaces are correct, because.IH.is not predefined for (LOGICAL,INTERVAL(16)) operands.
CODE EXAMPLE 2-8 Interval .IH.Operator Extension
cat ce2-8.f95f95 -xia ce2-8.f95a.outThe extension of the + operator in CODE EXAMPLE 2-9 is incorrect because the attempt is made to change the definition of the intrinsic
INTERVAL(+) operator, which is predefined for (INTERVAL,INTERVAL) type operands.
CODE EXAMPLE 2-9 User-defined interface that conflicts with the use of the intrinsic INTERVAL(+) operator.
cat ce2-9.f95f95 -xia ce2-9.f95In CODE EXAMPLE 2-10, the following
CODE EXAMPLE 2-10 User-defined interface conflicts with the intrinsic use ofS1interface is incorrect, because.IH.is predefined for(INTERVAL(4),INTERVAL(8))operands..IH..
cat ce2-10.f95MODULE MINTERFACE OPERATOR (.IH.)MODULE PROCEDURE S1END INTERFACECONTAINSINTERVAL FUNCTION S1(X, Y)INTERVAL(4), INTENT(IN) :: XINTERVAL(8), INTENT(IN) :: YS1 = [1.0]END FUNCTION S1END MODULE MPROGRAM TESTUSE MINTERVAL(4) :: X = [1.0]INTERVAL(8) :: Y = [2.0]PRINT *, 'X .IH. Y = ', X .IH. YEND PROGRAM TESTmath%f95 -xia ce2-10.f95MODULE M^"ce2-10.f95", Line = 1, Column = 8: ERROR: The compiler has detected errors in module "M". No module information file will be created for this module.MODULE PROCEDURE S1^"ce2-10.f95", Line = 3, Column = 22: ERROR: This specific interface "S1" conflicts with the intrinsic use of "ih".USE M^"ce2-10.f95", Line = 14, Column = 5: ERROR: Module "M" has compile errors, therefore declarations obtained from the module via the USE statement may be incomplete.f90: COMPILE TIME 0.190000 SECONDSf90: MAXIMUM FIELD LENGTH 4135778 DECIMAL WORDSf90: 18 SOURCE LINESf90: 3 ERRORS, 0 WARNINGS, 0 OTHER MESSAGES, 0 ANSIThe number of arguments of an operator function that extends an intrinsic
INTERVALoperator must agree with the number of operands needed for the intrinsic operator, as shown in CODE EXAMPLE 2-11.
CODE EXAMPLE 2-11 Incorrect change in the number of arguments in a predefined INTERVALoperator.
cat ce2-11.f95f95 -xia ce2-11.f95A binary intrinsic
INTERVALoperator cannot be extended with unary operator function having anINTERVALargument.In CODE EXAMPLE 2-12, the
S1interface is incorrect, because "+" is predefined for theINTERVALoperand.
CODE EXAMPLE 2-12 User-defined interface that conflicts with the intrinsic use of unary "+".
cat ce2-12.f95f95 -xia ce2-12.f95In a generic interface block, if the generic name specified in the
INTERFACEstatement is the name of an intrinsicINTERVALsubprogram, the specific user-defined subprograms extend the predefined meaning of the intrinsic subprogram.All references to subprograms having the same generic name must be unambiguous.
The intrinsic subprogram is treated as a collection of specific intrinsic subprograms, the interface definitions of which are also specified in the generic interface block.
CODE EXAMPLE 2-13 Correct extension of intrinsic INTERVALfunctionWID.
cat ce2-13.f95f95 -xia ce2-13.f95a.outCODE EXAMPLE 2-14 is correct.
CODE EXAMPLE 2-14 Correct extension of the intrinsicINTERVALfunctionABS.
cat ce2-14.f95MODULE MINTERFACE ABSMODULE PROCEDURE S1END INTERFACECONTAINSINTERVAL FUNCTION S1(X)INTERVAL, INTENT(IN) :: XS1 = [-1.0]END FUNCTION S1END MODULE MPROGRAM TESTUSE MINTERVAL :: X = [1, 2]PRINT *, ABS(X)END PROGRAM TESTmath%f95 -xia ce2-14.f95math%a.out[-1.0,-1.0]CODE EXAMPLE 2-15 is correct.
CODE EXAMPLE 2-15
Correct extension of the intrinsic
cat ce2-15.f95MODULE MINTERFACE MINMODULE PROCEDURE S1END INTERFACECONTAINSINTERVAL FUNCTION S1(X, Y)INTERVAL(4), INTENT(IN) :: XINTERVAL(8), INTENT(IN) :: YS1 = [-1.0]END FUNCTION S1END MODULE MPROGRAM TESTUSE MINTERVAL(4) :: X = [1, 2]INTERVAL(8) :: Y = [3, 4]REAL :: R = 0.1PRINT *, MIN(X, Y)END PROGRAM TESTmath%f95 -xia ce2-15.f95math%a.out[-1.0,-1.0]INTERVALfunctionMIN.2.8.1 Extended Operators with Widest-Need Evaluation
CODE EXAMPLE 2-16 illustrates how widest-need expression processing occurs when calling predefined versus extended versions of an intrinsic
CODE EXAMPLE 2-16 Widest-need expression processing when calling a predefined version of an intrinsicINTERVALoperator.INTERVALoperator.
cat ce2-16.f95MODULE MINTERFACE OPERATOR (.IH.)MODULE PROCEDURE S4END INTERFACECONTAINSINTERVAL FUNCTION S4(X, Y)COMPLEX, INTENT(IN) :: XCOMPLEX, INTENT(IN) :: YS4 = [0]END FUNCTION S4END MODULE MUSE MINTERVAL :: X = [1.0]REAL :: R = 1.0COMPLEX :: C = (1.0, 0.0)X = (R-0.1).IH.(R-0.2) ! intrinsic interval .IH. is invoked,! widest-need on both argumentsX = X .IH. (R+R) ! intrinsic interval .IH. is invoked,! widest-need on both argumentsX = X .IH. (R+R+X) ! intrinsic interval .IH. is invoked,! widest-need on the second argumentX = (R+R) .IH. (R+R+X) ! intrinsic interval .IH. is invoked,! widest-need on both argumentsX = C .IH. (C+R) ! s4 is invoked, no widest-needENDmath%f95 -xia ce2-16.f95math%a.outCODE EXAMPLE 2-17 illustrates how widest-need expression processing occurs when calling a user-defined operator.
CODE EXAMPLE 2-17 Widest-need expression processing when invoking a user-defined operator.
cat ce2-17.f952.8.2
INTERVAL(X[,Y,KIND])Description: Convert to
INTERVALtype.
Xis of typeINTEGER,REAL, orINTERVAL.
Y(optional) is of typeINTEGERorREAL. IfXis of typeINTERVAL,Ymust not be present.
KIND(optional) is a scalarINTEGERinitialization expression.Result characteristics:
INTERVALIf
KINDis present, its value is used to determine the result's KTPV; otherwise, the result's KTPV is the same as a default interval.Containment is guaranteed if
Xis an interval. For example, given
INTERVAL(16)::X,the result of
INTERVAL(X,KIND=4)contains theINTERVALX.However, given
REAL(8)X,Y, the result ofINTERVAL(X,Y,KIND=4)does not necessarily contain the internal intervalX.IH.Y.The reason is thatXandYcan beREALexpressions, the values of which cannot be guaranteed.The
INTERVALconstructor does not necessarily contain the value of a literalINTERVALconstant with the same endpoints. For example,INTERVAL(1.1,1.3)does not necessarily contain the external value ev([1.1,1.3]) = [1.1, 1.3]. The reason is that the internal values ofREALconstants are approximations with unknown accuracy.To construct an interval that always contains two
REALvalues, use the interval hull operator.IH., as shown in CODE EXAMPLE 2-18.Result value: The interval result value is a valid interval.
If
Yis absent andXis an interval, thenINTERVAL(X [,KIND])is an interval containingXandINTERVAL(X[,KIND])is an interval with left and right endpoints[XL,XU], where
XL = REAL(INF(X) [,KIND])rounded down, so thatXL.LE.INF(X)
XU = REAL(SUP(X)[,KIND])rounded up, so thatXU.GE.SUP(X).If both
XandYare present (and are therefore not intervals), thenINTERVAL(X,Y [,KIND])is an interval with left and right endpoints equal toREAL(X[,KIND])andREAL(Y[,KIND])respectively.
Note – In this case, rounding direction is not specified. Therefore, containment is not provided.
[
-inf,inf] is returned in two cases:
- If both
XandYare present andYis less thanX.- If either
XorYor both do not represent a mathematical integer or real number (for example, when one or bothREALarguments is aNaN).2.8.2.1 Limiting the Scope of Widest-Need
The intrinsic
INTERVALconstructor function can be used in two ways:
- To perform KTPV conversions of
INTERVALvariables or expressions- To insulate a non-
INTERVALexpression from mixed-modeINTERVALexpression evaluation.Given the non-
INTERVAL(REALorINTEGER) expression,EXP, the code
INTERVAL YEXP
REAL R
R =
Y = Ris the same as
INTERVAL YEXP
Y = INTERVAL()This is not the same as
INTERVAL YEXP
Y =The later will evaluate
EXPas an interval expression. In the first two code fragments, the expressionEXPis evaluated as a non-INTERVALexpression, and the result is used to construct a degenerate interval.With two arguments,
EXP1 andEXP2,INTERVAL(EXP1,EXP2) insulates both expressions from widest-need expression processing and constructs an interval with endpoints equal to the result of the non-INTERVALevaluation of the expressions.Including the KIND parameter makes it possible to control the KTPV of the result. This is most often needed under -strict expression processing where explicit KTPV conversions are necessary.
The intrinsic
INTERVALfunction with non-INTERVALarguments should be used with care. Whenever interval containment is desired, use the interval hull operator.IH., as shown in CODE EXAMPLE 2-18.The
INTERVALconstructor acts as a boundary betweenINTERVALandREALorINTEGERexpressions. On the non-INTERVALside of this boundary, accuracy (and therefore containment) guarantees cannot be enforced.
CODE EXAMPLE 2-18 Containment Using the .IH.Operator
cat ce2-18.f951 FORMAT(" A, B = ")f95 -xia ce2-18.f95a.outSee Section 2.8.2 INTERVAL (X [,Y, KIND]) for details on the use of the intrinsic
INTERVALconstructor function.2.8.2.2 KTPV-Specific Names of Intrinsic
INTERVALConstructor FunctionsAs shown in TABLE 2-11, the intrinsic
INTERVALconstructor function can be called using a KTPV-specific form that does not use the optional KIND parameter.
TABLE 2-11 KTPV Specific Forms of the Intrinsic INTERVALConstructor FunctionINTERVAL(X[,Y],KIND=8)orINTERVAL(X[,Y])INTERVAL(X[,Y],KIND=4)INTERVAL(X[,Y],KIND=16)
2.8.2.3 Intrinsic
INTERVALConstructor Function Conversion ExamplesThe three examples in this section illustrate how to use the intrinsic
INTERVALconstructor to perform conversions fromREALtoINTERVALtype data items. CODE EXAMPLE 2-19 shows thatREALexpression arguments of theINTERVALconstructor are evaluated usingREALarithmetic and are, therefore, insulated from widest-need expression evaluations.
CODE EXAMPLE 2-19 INTERVALConversion
cat ce2-19.f95f95 -xia ce2-19.f95a.outCODE EXAMPLE 2-19 notes:
- Lines 7 and 10: Interval
Xis assigned a degenerate interval with both endpoints equal to the internal representation of the real constant 0.1- Line 15: Interval
DXis assigned an interval with left and right endpoints equal to the result ofREALexpressionsR+SandT+R8respectively- Line 17: Interval
Yis converted to a containing KTPV-8 interval.CODE EXAMPLE 2-20 shows how the
CODE EXAMPLE 2-20 Create a narrow interval containing a given real number.INTERVALconstructor can be used to construct the smallest possible interval,Y, such that the endpoints ofYare not elements of a given interval,X.
cat ce2-20.f95INTERVAL :: X = [10.E-10,11.E+10]INTERVAL :: YY = INTERVAL(-TINY(INF(X)), TINY(INF(X))) + XPRINT *, X .INT. YENDmath%f95 -xia ce2-20math%a.outTGiven an interval
X, a sharp intervalYsatisfying the conditionX.INT.Yis constructed. For information on the interior set relation, Section 2.7.3 Interior: (X .INT. Y).CODE EXAMPLE 2-21 illustrates when the
CODE EXAMPLE 2-21INTERVALconstructor returns the interval [-INF,INF] and [MAX_FLOAT,INF].INTERVAL(NaN)
cat ce2-21.f95REAL :: R = 0., S = 0.T = R/S ! Line 2PRINT *, TPRINT *, INTERVAL(T, S) ! Line 4PRINT *, INTERVAL(T, T) ! Line 5PRINT *, INTERVAL(2., 1.) ! Line 6PRINT *, INTERVAL(1./R) ! Line 7ENDmath%f95 -xia ce2-21.f95math%a.outNaN[-Inf,Inf][-Inf,Inf][-Inf,Inf][1.7976931348623157E+308,Inf]CODE EXAMPLE 2-21 notes:
- Line 2: Variable
Tis assigned aNaNvalue.- Lines 4 and 5: One of the arguments of the
INTERVALconstructor is aNaNand the result is the interval[-INF,INF].- Line 6: The interval
[-INF,INF]is constructed instead of an invalid interval [2,1].- Line 7: The interval [
MAX_FLOAT,INF] is constructed that contains the interval [INF,INF]. See the supplementary paper [8] cited in Section 2.10 References, for a discussion of the chosen intervals to internally represent.2.8.3 Specific Names for Intrinsic Generic
INTERVALFunctionsThe
f95specific names for intrinsic genericINTERVALfunctions end with the generic name of the intrinsic and start withV, followed byS,D, orQfor arguments of typeINTERVAL(4),INTERVAL(8), andINTERVAL(16), respectively.In
f95,only the following specific intrinsic functions are supported for theINTERVAL(16)data type:VQABS,VQAINT,VQANINT,VQINF,VQSUP,VQMID,VQMAG,VQMIG, andVQISEMPTY.To avoid name space clashes in non-interval programs, the specific names are made available only by the command line options:
-xinterval-xinterval=strictor-xinterval=widestneed- macro
-xia,-xia=strictor-xia=widestneedSee Section 2.3.3 Interval Command-Line Options for more information.
All the supported intrinsic functions have specific names. For example, TABLE 2-12 lists the names for the
INTERVALversion of theABSintrinsic.
TABLE 2-12 Specific Names for the Intrinsic INTERVALABSFunctionVSABSINTERVAL(4)INTERVAL(4)VDABSINTERVAL(8)INTERVAL(8)VQABSINTERVAL(16)INTERVAL(16)
The remaining specific intrinsic functions are listed in Section 2.9.4.4 Intrinsic Functions.
2.9
INTERVALStatementsThis section describes the
INTERVALstatements recognized byf95. The syntax and description of each statement is given, along with possible restrictions and examples.2.9.1 Type Declaration
An
INTERVALstatement is used to declareINTERVALnamed constants, variables, and function results.INTERVALis an intrinsic numeric type declaration statement with the same syntax and semantics as standard numeric type declaration statements. The same specifications are available for use with theINTERVALstatement as exist for use in other numeric type declarations.Description: The declaration can be
INTERVAL,INTERVAL(4),INTERVAL(8), orINTERVAL(16).2.9.1.1
INTERVAL
INTERVAL :: Wthe variable,
W, has the defaultINTERVALKTPV of 8 and occupies 16 bytes of contiguous memory. In Sun WorkShop 6 Fortran 95, the defaultINTERVALKTPV is not altered by the command-line options-xtypemapor-r8const.CODE EXAMPLE 2-22 Illegal Derived Type:
INTERVALcannot be used as a derived type name. For example the code in CODE EXAMPLE 2-22 is illegal.INTERVAL
2.9.1.2
INTERVAL(n), for n{4, 8, 16}
INTERVAL(n) :: Wthe variable,
W, has KTPV = n and occupies 2n bytes of contiguous memory.CODE EXAMPLE 2-23 contains
CODE EXAMPLE 2-23 Declaring Intervals with Different KTPVsINTERVALvariable declarations with different KTPVs. Widest-need and strict value alignment is also shown.
cat ce2-23.f95INTERVAL(4) :: X1, X2INTERVAL(8) :: Y1, Y2INTERVAL(16) :: Z1, Z2REAL(8) :: D = 1.2345! Widest-need codeX1 = DY1 = DZ1 = D! Equivalent strict codeX2 = INTERVAL(INTERVAL(D, KIND=8), KIND=4)Y2 = INTERVAL(D, KIND=8)Z2 = INTERVAL(D, KIND=16)IF (X1 == X2) PRINT *, 'Check1'IF (Y1 == Y2) PRINT *, 'Check2'IF (Z1 == Z2) PRINT *, 'Check3'ENDmath%f95 -xia ce2-23.f95math%a.outCheck1Check2Check3CODE EXAMPLE 2-24 illustrates how to declare and initialize
CODE EXAMPLE 2-24 Declaring and InitializingINTERVALvariables. See Section 2.1.2 INTERVAL Constants regarding the different ways to representINTERVALconstants.INTERVALVariables
cat ce2-24.f95INTERVAL :: U = [1, 9.1_8], V = [4.1]! Widest-need codeINTERVAL :: W1 = 0.1_16! Equivalent strict codeINTERVAL :: W2 = [0.1_16]PRINT *, U, VIF (W1 .SEQ. W2) PRINT *, 'Check'ENDmath%f95 -xia ce2-24.f95math%a.out[1.0,9.1000000000000015] [4.0999999999999996,4.1000000000000006]CheckIn any initializing declaration statement, if the type of the data expression does not match the type of the symbolic name, type conversion is performed.
CODE EXAMPLE 2-25 DeclaringINTERVALArrays
2.9.1.3
DATAStatementsSyntax
The syntax for
CODE EXAMPLE 2-26DATAstatements containingINTERVALvariables is the same as for other numeric data types except thatINTERVALvariables are initialized usingINTERVALconstants.DATAStatement ContainingINTERVALVariables
2.9.1.4
EQUIVALENCEStatementsAny
INTERVALvariables or arrays may appear in anEQUIVALENCEstatement with the following restriction: If an equivalence set contains anINTERVALvariable or array, all of the objects in the equivalence set must have the same type, as shown in CODE EXAMPLE 1-18. This is a standard, not interval-specific, Fortran restriction.2.9.1.5
FORMATStatementsSyntax
The repeatable edit descriptors for intervals are:
Fw.d,VFw.d,Dw.d,VDw.d,Dw.dEe,VDw.dEe,Yw.d, andYw.dEe
D{
E,EN,ES,G}- w and e are nonzero, unsigned integer constants
- d is an unsigned integer constant.
See Section 2.9.2 Input and Output for the specifications of how edit descriptors process
INTERVALdata. For the behavior of standard edit descriptors with non-INTERVALdata, see the Fortran Reference Manual.All standard Fortran edit descriptors accept intervals. The prefix
Vcan be added to the standardE,F, andGedit descriptors for interval-only versions.As shown in CODE EXAMPLE 2-27, no modifications to nonrepeatable edit descriptors are required when reading or writing
CODE EXAMPLE 2-27 Nonrepeatable Edit Descriptor ExampleINTERVALdata.
cat ce2-27.f95INTERVAL :: X = [-1.3, 1.3]WRITE(*, '(SP, VF20.5)') XWRITE(*, '(SS, VF20.5)') XENDmath%f95 -xia ce2-27.f95math%a.out[-1.30001,+1.30001][-1.30001, 1.30001]Description
The repeatable edit descriptors
E,F,EN,ES,G,VE,VEN,VES,VF,VG,andYspecify howINTERVALdata are edited.CODE EXAMPLE 2-28 contains examples of
CODE EXAMPLE 2-28 Format Statements withINTERVAL-specific edit descriptors.INTERVAL-specific Edit Descriptors
See Section 2.9.2 Input and Output for additional examples.
2.9.1.6
FUNCTION(External)As shown in CODE EXAMPLE 2-29, there is no difference between an interval and a non-interval external function, except for the use of
CODE EXAMPLE 2-29 Default Interval FunctionINTERVALtypes (INTERVAL,INTERVAL(4),INTERVAL(8), orINTERVAL(16)) in the function's and argument's definitions.
The default
CODE EXAMPLE 2-30 ExplicitINTERVALin line 1 can be made explicit, as shown in CODE EXAMPLE 2-30.INTERVAL(16)Function Declaration
2.9.1.7
IMPLICITAttributeUse the
IMPLICITattribute to specify the default type of interval names.
IMPLICIT INTERVAL(8)(V)2.9.1.8
INTRINSICStatementUse the
CODE EXAMPLE 2-31 Intrinsic Function DeclarationINTRINSICstatement to declare intrinsic functions, so they can be passed as actual arguments.
Note – Specific names of generic functions must be used in theINTRINSICstatement and passed as actual arguments. See Section 2.8.3 Specific Names for Intrinsic Generic INTERVAL Functions and Section 2.9.4.4 Intrinsic Functions.
Because they are generic, the following intrinsic
INTERVALfunctions cannot be passed as actual arguments:
NDIGITS, INTERVAL2.9.1.9
NAMELISTStatementThe
CODE EXAMPLE 2-32NAMELISTstatement supports intervals.INTERVALSin aNAMELIST
2.9.1.10
PARAMETERAttributeThe
PARAMETERattribute is used to assign the result of anINTERVALinitialization to a named constant (PARAMETER).Syntax
PARAMETER(p=e [, p=expr]...)
- p
INTERVALsymbolic nameexprINTERVALconstant expression=assigns the value of e to the symbolic name, pDescription
Both the symbolic name, p, and the constant expression,
expr, must haveINTERVALtypes.Exponentiation to an integer power is allowed in constant expressions.
Mixed-mode
INTERVALexpression evaluation is supported in the definition of interval named constants under widest-need expression processing. If the constant expression's type does not match the named constant's type, type conversion of the constant expression is performed under widest-need expression processing.
Caution – Inf95, non-INTERVALconstant expressions are evaluated at compile time without regard to their possible subsequent use in mixed-modeINTERVALexpressions. They are outside the scope of widest-need expression processing. Therefore, no requirement exists to contain the value of the point expression used to set the value of non-INTERVALnamed constants. To remind users whenever a non-INTERVALnamed constant appears in a mixed-modeINTERVALexpression, a compile-time warning message is issued. Named constants, as defined by the Fortran standard, are more properly called read-only variables. There is no external value associated with a read-only variable.
In standard Fortran 95, named constants cannot be used to represent the infimum and supremum of an
CODE EXAMPLE 2-33 Constant Expression in Non-INTERVALconstant. This is a known error that this constraint is not enforced in this release.INTERVALPARAMETERAttribute
cat ce2-33.f95REAL(4), PARAMETER :: R = 0.1INTERVAL(4), PARAMETER :: I4 = 0.1INTERVAL(16), PARAMETER :: I16 = 0.1INTERVAL :: XR, XIXR = R4XI = I4IF ((.NOT.(XR.SP.I16)).AND. (XI.SP.I16)) PRINT *, 'Check.'ENDmath%f95 -xia ce2-33.f95math%a.outCheck.
Note –XRdoes not contain 1/10, whereasXIdoes.
2.9.1.11 Fortran 95-Style
POINTERIntervals can be associated with pointers.
CODE EXAMPLE 2-34INTERVALPointers
2.9.1.12 Statement Function
A statement function can be used to declare and evaluate parameterized
CODE EXAMPLE 2-35INTERVALexpressions. Non-INTERVALstatement function restrictions apply.INTERVALStatement Function
cat ce2-35.f95INTERVAL :: X, FF(X) = SIN(X)**2 + COS(X)**2IF(1 .IN. F([0.5])) PRINT *, 'Check'ENDmath%f95 -xia ce2-35.f95math%a.outCheck2.9.1.13 Type Statement
The type statement specifies the data type of variables in a variable list. Optionally the type statement specifies array dimensions, and initializes variables with values.
Syntax
The syntax is the same as for non-
INTERVALnumeric data types, except that type can be one of the followingINTERVALtype specifiers:INTERVAL,INTERVAL(4), INTERVAL(8),orINTERVAL(16).Description
Properties of the type statement are the same for
INTERVALtypes as for other numeric data types.Restrictions
Same as for non-
CODE EXAMPLE 2-36INTERVALnumeric types.INTERVALType Statement
CODE EXAMPLE 2-36 notes:
Jis initialized to [0.0]Kis initialized to an interval containing [0.1, 0.2]Lis initialized to an interval containing [0.1]2.9.1.14
WRITEStatementThe
WRITEstatement acceptsINTERVALvariables and processes an input/output list in the same way that non-INTERVALtype variables are processed. Formatted writing ofINTERVALdata is performed using the definedINTERVALedit descriptors.NAMELIST-directedWRITEstatements support intervals.2.9.1.15
READStatementThe
READstatement acceptsINTERVALvariables and processes an input/output list in the same way that non-INTERVALtype variables are processed.2.9.2 Input and Output
The process of performing
INTERVALinput/output is the same as for other non-INTERVALdata types.2.9.2.1 External Representations
Let x be an external (decimal) number that can be read or written using either list-directed or formatted input/output. See the subsections in Section 2.1 "Fortran Extensions" regarding the regarding the distinction between internal approximations and external values. Such a number can be used to represent either an external interval, or an endpoint. There are three displayable forms of an external interval:
[X_inf,X_sup]represents the mathematical interval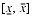
[X]represents the degenerate mathematical interval, or [x]
Xrepresents the non-degenerate mathematical interval [x] + [-1,+1]uld (unit in the last digit). This form is the single-number representation, in which the last decimal digit is used to construct an interval (see theYedit descriptor). In this form, trailing zeros are significant. Thus0.10represents interval[0.09,0.11],100E-1represents interval[9.9,10.1], and0.10000000represents the interval[0.099999999,0.100000001].A positive or negative infinite interval endpoint is input/output as a case-insensitive string
INForINFINITYprefixed with a minus or an optional plus sign.The empty interval is input/output as the case-insensitive string
EMPTYenclosed in square brackets,"[...]". The string,EMPTY,may be preceded or followed by blanks.CODE EXAMPLE 1-6 can be used to experiment with extended intervals.
See Section 2.4.1 Arithmetic Operators +, -, *, /, for more details.
2.9.2.2 Input
On input, any external interval,
X, or its components,X_infandX_sup, can be formatted in any way that is accepted by theDw.d edit descriptor. Therefore, let input-field, input-field1, and input-field2 be valid input fields for theDw'.d,Dw1.d, andDw2.d edit descriptors, respectively.Let w be the width of an interval input field. On input, w must be greater than zero. All
INTERVALedit descriptors accept inputINTERVALdata in each of the following three forms:
- [input-field1, input-field2], in which case w1 + w2 = w - 3 or w = w1 + w2 + 3
- [input-field], in which case w' = w-2 or w = w'+2
- input-field, in which case w' = w
The first form (two numbers enclosed in brackets and separated by a comma) is the familiar [inf, sup] representation.
The second form (a single number enclosed in brackets) denotes a point or degenerate interval.
The third form (without brackets) is the single-number form of an interval in which the last displayed digit is used to determine the interval's width. See Section 2.9.2.7 Single-Number Editing with the Y Edit Descriptor. For more detailed information, see M. Schulte, V. Zelov, G.W. Walster, D. Chiriaev, "Single-Number Interval I/O," Developments in Reliable Computing, T. Csendes (ed.), (Kluwer 1999).
If an infimum is not internally representable, it is rounded down to an internal approximation known to be less than the exact value. If a supremum is not internally representable, it is rounded up to an internal approximations known to be greater than the exact input value. If the degenerate interval is not internally representable, it is rounded down and rounded up to form an internal
INTERVALapproximation known to contain the exact input value.2.9.2.3 List-Directed Input
If an input list item is an
INTERVAL, the corresponding element in the input record must be an external interval or a null value.An external interval value may have the same form as an
INTERVAL,REAL, orINTEGERliteral constant. If an interval value has the form of aREALorINTEGERliteral constant with no enclosing square brackets, "["... "]", the external interval is interpreted using the single-number interval representation: [x] + [-1,1]uld (unit in the last digit).When using the [inf, sup] input style, an end of record may occur between the infimum and the comma or between the comma and the supremum.
A null value, specified by two consecutive commas, means that the corresponding
INTERVALlist item is unchanged.
Note – Do not use a null value for the infimum or supremum of an interval.
CODE EXAMPLE 2-37 List Directed Input/Output Code
cat ce2-37.f95INTERVAL, DIMENSION(6) :: XINTEGER IDO I = LBOUND(X, 1), UBOUND(X, 1)READ(*, *) X(I)WRITE(*, *) X(I)END DOENDmath%f95 -xia ce2-37.f95math%a.out1.234500[1.2344989999999997,1.2345010000000001][1.2345][1.2344999999999999,1.2345000000000002][-inf,2][-Inf,2.0][-inf][-Inf,-1.7976931348623157E+308][EMPTY][EMPTY][1.2345,1.23456][1.2344999999999999,1.2345600000000002]2.9.2.4 Formatted Input/Output
The
INTERVALedit descriptors are:
Ew.dEeENw.dESw.dFw.dGw.dEeVEw.dEeVENw.dEeVESw.dEeVFw.dVGw.dEYw.dEeIn the
INTERVALedit descriptors:
- w specifies the number of positions occupied by the field
- d specifies the number of digits to the right of the decimal point
Ee specifies the width of exponent fieldThe parameters w and d must be used.
Ee is optionalThe w and d specifiers must be present and are subject to the following constraints:
- e > 0
- w
0 when using the
Fedit descriptor, or w > 0 when using all edit descriptors other thanF.Input Actions
Input actions for formatted interval input are the same as for other numeric data types, except that in all cases, the stored internal approximation contains the external value represented by the input character string. Containment can require outward rounding of interval endpoints. Given any input interval characters,
input_string, the corresponding external value, ev(input_string), and the resulting internal approximation after input conversion,X, are related:
- ev(
input_string)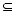
X.During input, all interval edit descriptors have the same semantics. The value of parameter w, is the field width containing the external interval. The value of e is ignored.
Output Actions
Output actions for formatted interval output are the same as for other data types, except that in all cases, the mathematical value of the output character string must contain the mathematical value of the internal data item in the output list. Containment can require outward rounding of interval endpoints. Given any internal interval,
X, the corresponding output characters,output_string, and the external value, ev(output_string), are related:
Xev(
output_string).During output, edit descriptors cause the internal value of interval output list items to be displayed using different formats. However, the containment constraint requires that
- ev(
input_string)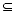
Xev(
output_string)2.9.2.5 Formatted Input
The behavior of formatted input is identical for all
INTERVALedit descriptors listed in Section 2.9.2.4 Formatted Input/Output. All inputs described in Section 2.9.2.2 Input are accepted.If the input field contains a decimal point, the value of d is ignored. If a decimal point is omitted from the input field, d determines the position of the decimal point in the input value; that is, the input value is read as an integer and multiplied by 10(-d).
CODE EXAMPLE 2-38 The decimal point in an input value dominates format specifiers.
CODE EXAMPLE 2-39 All the
cat ce2-38.f95INTERVAL :: X, YREAD(*, '(F10.4)') XREAD(*, '(F10.4)') YWRITE(*, *)'1234567890123456789012345678901234567890-position'WRITE(*, '(1X, E19.6)') XWRITE(*, '(1X, E19.6)') YENDmath%f95 -xia ce2-38.f95math%a.out[.1234][1234]1234567890123456789012345678901234567890-position0.123400E+0000.123400E+000INTERVALedit descriptors accept single-number input
.
cat ce2-39.f95INTERVAL, DIMENSION(9) :: XINTEGER :: IREAD(*, '(Y25.3)') X(1)READ(*, '(E25.3)') X(2)READ(*, '(F25.3)') X(3)READ(*, '(G25.3) ') X(4)READ(*, '(VE25.3)') X(5)READ(*, '(VEN25.3)') X(6)READ(*, '(VES25.3)') X(7)READ(*, '(VF25.3)') X(8)READ(*, '(VG25.3)') X(9)DO I = LBOUND(X, 1), UBOUND(X, 1)PRINT *, X(I)END DOENDmath%f95 -xia ce2-39.f95math%a.out1.231.231.231.231.231.231.231.231.23[1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003][1.2199999999999999,1.2400000000000003]Blank Editing (BZ)
Because trailing zeros are significant in single-number
CODE EXAMPLE 2-40INTERVALinput, theBZcontrol edit descriptor is ignored when processing leading and trailing blanks for input toINTERVALlist items.BZDescriptor
cat ce2-40.f95INTERVAL :: XREAL(4) :: RREAD(*, '(BZ, F40.6 )') XREAD(*, '(BZ, F40.6 )') RWRITE(*, '(VF40.3)') XWRITE(*, '(F40.3)') RENDmath%f95 -xia ce2-40.f95math%a.out[.9998 ].9998[ 0.999, 1.000]1.000Scale Factor (P)
The
Pedit descriptor changes the scale factor forY,VE,VEN,VES,VF, andVGdescriptors and forF,E,EN,ES, andGedit descriptors when applied to intervals. ThePedit descriptor scales interval endpoints the same way it scalesREALvalues.2.9.2.6 Formatted Output
The
F,E, andGedit descriptors applied to intervals have the same meaning as theYedit descriptor except that if theForGedit descriptor is used, the output field may be formatted using theFedit descriptor. If theEedit descriptor is used, the output field always has the form prescribed by theEedit descriptor.Formatted
INTERVALoutput has the following properties:
- A positive interval endpoint starts with an optional plus sign.
- A negative endpoint always starts with a leading minus sign.
- A zero interval endpoint never starts with a leading plus or minus.
- The
VF,VEandVGedit descriptors provide [inf, sup]-style formatting of intervals.- The
Yedit descriptor produces single-number interval output.- If an output list item matching the
VF,VE,VG,orYedit descriptor is any type other thanINTERVAL, the entire output field is filled with asterisks.- If the output field's width, w, in
VF,VE,orVGedit descriptors is an even number, the field is filled with one leading blank character and w-1 is used for the output field's width.On output, the default values for the exponent field, e, are shown in TABLE 2-13.
TABLE 2-13 Default Values for Exponent Field in Output Edit Descriptors Y,E,EN,ES,G3 3 3 VE,VEN,VES,VG2 2 3
2.9.2.7 Single-Number Editing with the
YEdit DescriptorThe
Yedit descriptor formats extended interval values in the single-number form.If the external
INTERVALvalue is not degenerate, the output format is the same as for aREALorINTEGERliteral constant (Xwithout square brackets, "["..."]"). The external value is interpreted as a non-degenerate mathematical interval [x] + [-1,1]uld. The general form of theYedit descriptor is:
Yw.dEeThe d specifier sets the number of places allocated for displaying significant digits. However, the actual number of displayed digits may be more or less than d, depending on the value of w and the width of the external interval.
The e specifier (if present) defines the number of places in the output subfield reserved for the exponent.
The presence of the e specifier forces the output field to have the form prescribed by the
E(as opposed toF) edit descriptor.The single-number interval representation is often less precise than the [inf, sup] representation. This is particularly true when an interval or its single-number representation contains zero or infinity.
For example, the external value of the single-number representation for [-15, +75] is ev(
[0E2]) = [-100, +100]. The external value of the single-number representation for [1,] is ev(
[0E+inf]) =.
In these cases, to produce a narrower external representation of the internal approximation, the
CODE EXAMPLE 2-41VGw.d'Ee edit descriptor is used, with d'1 to display the maximum possible number of significant digits within the w-character input field.
Y[inf, sup]-style Output
cat ce2-41.f95INTERVAL :: X = [-1, 10]INTERVAL :: Y = [1, 6]WRITE(*, '(Y20.5)') XWRITE(*, '(Y20.5)') YENDmath%f95 -xia ce2-41.f95math%a.out[-1. ,0.1E+002][1.0 ,6.0 ]If it is possible to represent a degenerate interval within the w-character output field, the output string for a single number is enclosed in obligatory square brackets, "
[", ... "]" to signify that the result is a point.If there is sufficient field width, the
CODE EXAMPLE 2-42EorFedit descriptor is used, depending on which can display the greater number of significant digits. If the number of displayed digits using theEandFedit descriptor is the same, theFedit descriptor is used.Yw.d Output
math% cat ce2-42.f95WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1x, F20.6)') [1.2345678, 1.23456789]WRITE(*, '(1x, F20.6)') [1.234567, 1.2345678]WRITE(*, '(1x, F20.6)') [1.23456, 1.234567]WRITE(*, '(1x, F20.6)') [1.2345, 1.23456]WRITE(*, '(1x, F20.6)') [1.5111, 1.5112]WRITE(*, '(1x, F20.6)') [1.511, 1.512]WRITE(*, '(1x, F20.6)') [1.51, 1.52]WRITE(*, '(1x, F20.6)') [1.5, 1.5]ENDmath%f95 -xia ce2-42.f95math%a.out1234567890123456789012345678901234567890-position1.23456791.2345671.234561.23451.5111.511.5[ 1.50000000000]Increasing interval width decreases the number of digits displayed in the single-number representation. When the interval is degenerate all remaining positions are filled with zeros and brackets are added if the degenerate interval value is represented exactly.
The intrinsic function
NDIGITS(see TABLE 2-21) returns the maximum number of significant digits necessary to write anINTERVALvariable or array using the single-number display format.
CODE EXAMPLE 2-43 Yw.d Output Using theNDIGITSIntrinsic
cat ce2-43.f95f95 -xia ce2-43.f95a.outFor readability, the decimal point is always located in position p = e + d + 4, counting from the right of the output field.
CODE EXAMPLE 2-44 {Y,F,E,G}w.d output, where d sets the minimum number of significant digits to be displayed.
cat ce2-44.f95INTERVAL :: X = [1.2345678, 1.23456789]INTERVAL :: Y = [1.5]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, F20.5)') XWRITE(*, '(1X, F20.5)') YWRITE(*, '(1X, 1E20.5)') XWRITE(*, '(1X, 1E20.5)') YWRITE(*, '(1X, G20.5)') XWRITE(*, '(1X, G20.5)') YWRITE(*, '(1X, Y20.5)') XWRITE(*, '(1X, Y20.5)') YENDmath%f95 -xia ce2-44.f95math%a.out1234567890123456789012345678901234567890-position1.2345679[ 1.5000000000]0.12345E+001[ 0.15000E+001]1.2345679[ 1.5000000000]1.2345679[ 1.5000000000]The optional e specifier specifies the number of exponent digits. If the number of exponent digits is specified, w must be at least d + e + 7.
CODE EXAMPLE 2-45Yw.dEe output (the usage of e specifier)
.
cat ce2-45.f95INTERVAL :: X = [1.2345, 1.2346]INTERVAL :: Y = [3.4567, 3.4568]INTERVAL :: Z = [1.5]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, Y19.5E4)') XWRITE(*, '(1X, Y19.5E4)') YWRITE(*, '(1X, Y19.5E4)') ZWRITE(*, '(1X, Y19.5E3)') XWRITE(*, '(1X, Y19.5E3)') YWRITE(*, '(1X, Y19.5E3)') ZENDmath%f95 -xia ce2-45.f95math%a.out1234567890123456789012345678901234567890-position0.1234 E+00010.3456 E+0001[ 0.15000E+0001]0.1234 E+0010.3456 E+001[ 0.15000E+001]2.9.2.8
EEdit DescriptorThe
Eedit descriptor formatsINTERVALdata items using the single-numberEform of theYedit descriptor.
Ew.dEe
CODE EXAMPLE 2-46 Ew.dEe Edit Descriptor
cat ce2-46.f95f95 -xia ce2-46.f95a.out2.9.2.9
FEdit DescriptorThe
Fedit descriptor formatsINTERVALdata items using only theFform of theINTERVALYedit descriptor. The general form is:
Fw.dUsing the
CODE EXAMPLE 2-47Fdescriptor, it is possible to display more significant digits than specified by d. Positions corresponding to the digits that are not displayed are filled with blanks.Fw.d Edit Descriptor
cat ce2-47.f95INTERVAL :: X = [1.2345678, 1.23456789]INTERVAL :: Y = [2.0]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, F20.4)') XWRITE(*, '(1X, E20.4)') XWRITE(*, '(1X, F20.4)') YWRITE(*, '(1X, E20.4)') YENDmath%f95 -xia ce2-47.f95math%a.out1234567890123456789012345678901234567890-position1.23456790.1234E+001[ 2.000000000][ 0.2000E+001]2.9.2.10
GEdit DescriptorThe
Gedit descriptor formatsINTERVALdata items using the single-numberEorFform of theYedit descriptor. The general form is:CODE EXAMPLE 2-48
Gw.dEeGw.dEe Edit Descriptor
cat ce2-48.f95INTERVAL :: X = [1.2345678, 1.23456789]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, G20.4)') XWRITE(*, '(1X, G20.4E3)') XENDmath%f95 -xia ce2-48.f95math%a.out1234567890123456789012345678901234567890-position1.23456790.1234E+001
Note – If it is impossible to output interval endpoints according to theFdescriptor,Gedit descriptor uses theEdescriptor
2.9.2.11
VEEdit DescriptorThe general form of the
VEedit descriptor is:
VEw.dEeLet
Xdbe a valid external value using theEw'.d edit descriptor. TheVEedit descriptor outputsINTERVALdata items in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .The external values,
CODE EXAMPLE 2-49X_infandX_sup, are lower and upper bounds, respectively, on the infimum and supremum of theINTERVALoutput list item.VEOutput
cat ce2-49.f95INTERVAL :: X = [1.2345Q45, 1.2346Q45]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, VE25.3)') XWRITE(*, '(1X, VE33.4E4)') XENDmath%f95 -xia ce2-49.f95math%a.out1234567890123456789012345678901234567890-position[ 0.123E+046, 0.124E+046][ 0.1234E+0046, 0.1235E+0046]2.9.2.12
VENEdit DescriptorThe general form of the
VENedit descriptor is:
VENw.dEeLet
X_infandX_supbe valid external values displayed using theENw'.d edit descriptor. TheVENedit descriptor outputs anINTERVALdata item in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .The external values,
CODE EXAMPLE 2-50X_infandX_sup, are lower and upper bounds, respectively, on the infimum and supremum of theINTERVALoutput list item.VENOutput
cat ce2-50.f95INTERVAL :: X = [1024.82]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, VEN25.3)') XWRITE(*, '(1X, VEN33.4E4)') XENDmath%f95 -xia ce2-50.f95math%a.out1234567890123456789012345678901234567890-position[ 1.024E+003, 1.025E+003][ 1.0248E+0003, 1.0249E+0003]2.9.2.13
VESEdit DescriptorThe general form of the
VESedit descriptor is:
VESw.dEeLet
X_infandX_supbe a valid external values using theESw'.d edit descriptor. TheVESedit descriptor outputs anINTERVALdata item in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .The external values,
CODE EXAMPLE 2-51X_infandX_sup, are lower and upper bounds, respectively, on the infimum and supremum of theINTERVALoutput list item.VESOutput
cat ce2-51.f95INTERVAL :: X = [21.234]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, VES25.3)') XWRITE(*, '(1X, VES33.4E4)') XENDmath%f95 -xia ce2-51.f95math%a.out1234567890123456789012345678901234567890-position[ 2.123E+001, 2.124E+001][ 2.1233E+0001, 2.1235E+0001]2.9.2.14
VFEdit DescriptorLet
X_infandX_supbe valid external values displayed using theFw'.d edit descriptor. TheVFedit descriptor outputsINTERVALdata items in the following form:
[X_inf,X_sup], where w' = (w-3)/2 .The external values,
CODE EXAMPLE 2-52X_infandX_sup, are lower and upper bounds, respectively, on the infimum and supremum of theINTERVALoutput list item.VFOutput Editing
cat ce2-52.f95INTERVAL :: X = [1.2345, 1.2346], Y = [1.2345E11, 1.2346E11]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, VF25.3)') XWRITE(*, '(1X, VF25.3)') YENDmath%f95 -xia ce2-52.f95math%a.out1234567890123456789012345678901234567890-position[ 1.234, 1.235][***********,***********]
Note – If it is impossible to output an interval according to the specified format statement, asterisks are printed.
2.9.2.15
VGEdit DescriptorFor
CODE EXAMPLE 2-53INTERVALoutput,VGediting is the same asVEorVFediting, except that theGedit descriptor is used to format the displayed interval endpoints.VGOutput
cat ce2-53.f95INTERVAL :: X = [1.2345, 1.2346], Y = [1.2345E11, 1.2346E11]WRITE(*, *) '1234567890123456789012345678901234567890-position'WRITE(*, '(1X, VG25.3)') XWRITE(*, '(1X, VG25.3)') YENDmath%f95 -xia ce2-53.f95math%a.out1234567890123456789012345678901234567890-position[ 1.23 , 1.24 ][ 0.123E+012, 0.124E+012]
Note – If it is impossible to output interval endpoints according to theFdescriptor, theVGedit descriptor uses theEdescriptor.
2.9.2.16 Unformatted Input/Output
Unformatted input/output is used to transfer data to and from memory locations without changing its internal representation. With intervals, unformatted input/output is particularly important, because outward rounding on input and output is avoided.
Note – Use only unformattedINTERVALinput and output to read and write unformattedINTERVALdata. Binary file compatibility with future releases is not guaranteed. Unformatted input/output relies on the fact thatINTERVALdata items are opaque.
2.9.2.17 List-Directed Output
REALconstants for left and right endpoints are produced using either anFor anEedit descriptor. Let |x| be the absolute value of an output interval endpoint. Then if
,
the endpoint is produced using the
0PFw.d edit descriptor. Otherwise, the1PEw.dEe descriptor is used. Inf95, d1=-2and d2=+8.For the output of
INTERVALdata items inf95, the values for d and e are the same as for theREALtypes with the same KTPV. The value of w reflects the need to conveniently accommodate twoREALvalues and three additional characters for square brackets, "[", "]", and the comma, as shown in CODE EXAMPLE 2-37.2.9.2.18 Single-Number Input/Output and Base Conversions
Single-number
INTERVALinput, immediately followed by output, can appear to suggest that a decimal digit of accuracy has been lost, when in fact radix conversion has caused a 1 or 2 ulp increase in the width of the stored input interval. For example, an input of 1.37 followed by an immediate print will result in 1.3 being output. See Section 2.9.2.4 Formatted Input/Output.As shown in CODE EXAMPLE 1-6, programs must use character input and output to exactly echo input values and internal reads to convert input character strings into valid internal approximations.
2.9.3 Intrinsic
INTERVALFunctionsThis section contains the defining properties of the
f95intrinsicINTERVALfunctions.Generic intrinsic
INTERVALfunctions that accept arguments with more than one KTPV have both generic and KTPV-specific names. When an intrinsic function is invoked using its KTPV-specific name, arguments must have the matching KTPV.
Note – Inf95, some KTPV-16 specific intrinsic functions are not provided. This is an outstanding quality of implementation opportunity.
With functions that accept more than one
INTERVALdata item (for example,SIGN(A,B)), all arguments must have the same KTPV. Under widest-need expression processing, compliance with this restriction is automatic. With strict expression processing, developers are responsible for enforcing type and KTPV restrictions on intrinsic function arguments. Compile-time errors result when different KTPVs are encountered.2.9.4 Mathematical Functions
This section lists the type-conversion, trigonometric, and other functions that accept
INTERVALarguments. The symbolsand
in the interval
are used to denote its ordered elements, the infimum, or lower bound and supremum, or upper bound, respectively. In point (non-interval) function definitions, lowercase letters x and y are used to denote
REALorINTEGERvalues.When evaluating a function, f, of an interval argument, X, the interval result, f(X), must be an enclosure of its containment set, cset(f, {x}), where:
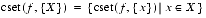
A similar result holds for functions of n-variables. Determining the containment set of values that must be included when the interval
contains values outside the domain of f is discussed in the supplementary paper [1] cited in Section 2.10 References. The results therein are needed to determine the set of values that a function can produce when evaluated on the boundary of, or outside its domain of definition. This set of values, called the containment set is the key to defining interval systems that return valid results, no matter what the value of a function's arguments or an operator's operands. As a consequence, there are no argument restrictions on any intrinsic
INTERVALfunctions inf95.2.9.4.1 Inverse Tangent Function
ATAN2(Y,X)This sections provides additional information about the inverse tangent function. For further details, see the supplementary paper [9] cited in Section 2.10 References.
Description: Interval enclosure of the inverse tangent function over a pair of intervals.
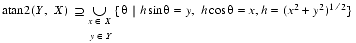
Special values: TABLE 2-14 and CODE EXAMPLE 2-54 display the
ATAN2indeterminate forms.
TABLE 2-14 ATAN2Indeterminate Forms0 0 [-1, 1] [-1, 1] 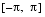
+ + [0, 1] [0, 1] 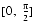
+ - [0, 1] [-1, 0] 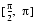
- - [-1, 0] [-1, 0] 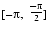
- + [-1, 0] [0, 1] 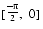
CODE EXAMPLE 2-54 ATAN2Indeterminate Forms
cat ce2-54.f951 FORMAT("Y, X = ?")f95 -xia ce2-54.f95a.out[0] [0]inf infinf -inf-inf +inf-inf -infArguments:
Yis of typeINTERVAL.Xis of the same type andKINDtype parameter asY.Result characteristics: Same as the arguments.
Result value: The interval result value is an enclosure for the specified interval. An ideal enclosure is an interval of minimum width that contains the exact mathematical interval in the description.
The result is empty if one or both arguments are empty.
In the case where x < 0 and
, to get a sharp interval enclosure (denoted by
), the following convention uniquely defines the set of all possible returned interval angles:

This convention, together with

results in a unique definition of the interval angles
that
ATAN2(Y,X)must include.TABLE 2-15 contains the tests and arguments of the
REALATAN2function that are used to compute the endpoints ofin the algorithm that satisfies the constraints required to produce sharp interval angles. The first two columns define the distinguishing cases. The third column contains the range of possible values of the midpoint, m(
), of the interval
. The last two columns show how the endpoints of
are computed using the
REALATAN2intrinsic function. Directed rounding must be used to guarantee containment.
TABLE 2-15 Tests and Arguments of the REALATAN2Function- < y
x < 0 
ATAN2(y, x)ATAN2(, x) + 2
- = y
x < 0 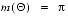
ATAN2(y, x)2 - q
< -
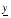
x < 0 
ATAN2(y, x) - 2ATAN2(, x)
2.9.4.2 Maximum:
MAX(X1,X2,[X3,...])Description: Range of maximum.
The containment set for max(X1, ..., Xn) is:
.
The implementation of the
MAXintrinsic must satisfy:
MAX(X1,X2,[X3, ...]){max(X1, ..., Xn)}.
Arguments: The arguments are of type
INTERVALand have the same type andKINDtype parameter.Result characteristics: The result is of type
INTERVAL. The kind type parameter is that of the arguments.2.9.4.3 Minimum:
MIN(X1,X2,[X3, ...])Description: Range of minimum.
The containment set for min(X1, ..., Xn) is:
.
The implementation of the
MINintrinsic must satisfy:
MIN(X1,X2,[X3, ...]){min(X1, ..., Xn)}.
Arguments: The arguments are of type
INTERVALand have the same type andKINDtype parameter.Result characteristics: The result is of type
INTERVAL. The kind type parameter is that of the arguments.2.9.4.4 Intrinsic Functions
Tables TABLE 2-17 through TABLE 2-21 list the properties of intrinsic functions that accept interval arguments. TABLE 2-16 lists the tabulated properties of intrinsic
INTERVALfunctions in these tables.
TABLE 2-16 Tabulated Properties of Each Intrinsic INTERVALFunctionTabulated Property Description Intrinsic Function what the function does Definition mathematical definition No. of Args. number of arguments the function accepts Generic Name the function's generic name Type-Specific Names the function's specific names Argument Type data type associated with each specific name Function Type data type returned for specific argument data type
KTPV 4, 8 and 16 versions of intrinsic
INTERVALfunctions are defined. The corresponding specific intrinsic names begin withVS,VDorVQ, frominterValSingle, Double and Quad.For each specific
REALintrinsic function, a corresponding intrinsicINTERVALfunction exists with aVS,VD,orVQprefix, such asVSSIN()andVDSIN().Because indeterminate forms are possible, special values of the X**Y and ATAN2 function are contained in Section 2.5 Power Operators X**N and X**Y and Section 2.9.4.1 Inverse Tangent Function ATAN2(Y,X), respectively. The remaining intrinsic functions do not require this treatment.
TABLE 2-17 Intrinsic INTERVALArithmetic FunctionsAbsolute value |a| 1 ABSVDABSVSABSVQABSINTERVAL(8)INTERVAL(4)INTERVAL(16)INTERVAL(8)INTERVAL(4)INTERVAL(16)Truncation See Note 1 int(a) 1 AINTVDINTVSINTVQINTINTERVAL(8)INTERVAL(4)INTERVAL(16)INTERVAL(8)INTERVAL(4)INTERVAL(16)Nearest integer int(a + .5)
if a0
int(a - .5)
if a < 01 ANINTVDNINTVSNINTVQNINTINTERVAL(8)INTERVAL(4)INTERVAL(16)INTERVAL(8)INTERVAL(4)INTERVAL(16)Remainder a-b(int(a/b)) 2 MODVDMODVSMODINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Transfer of sign See Note 2 |a| sgn(b) 2 SIGNVDSIGNVSSIGNINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Choose largest value See Note 3 max(a,b,...) 2
MAXMAXINTERVALINTERVALChoose smallest value See Note 3 min(a,b,...) 2
MINMININTERVALINTERVAL(1) int(a) = floor(a) if a > 0 and ceiling(a) if a < 0 (2) The signum function sgn(a) = -1 if a < 0, +1 if a > 0 and 0 if a = 0 (3) The MINandMAXintrinsic functions ignore empty interval arguments unless all arguments are empty, in which case, the empty interval is returned.
TABLE 2-18 Intrinsic INTERVALType Conversion FunctionsINTERVAL1, 2, or 3 INTERVALINTERVAL
INTERVAL(4)
INTERVAL(8)
INTEGER
REAL
REAL(8)
REAL(16)INTERVAL
INTERVAL
INTERVAL
INTERVAL
INTERVAL
INTERVAL
INTERVALINTERVAL(4)1 or 2 SINTERVALINTERVAL
INTERVAL(4)
INTERVAL(8)
INTEGER
REAL
REAL(8)
REAL(16)INTERVAL(4)
INTERVAL(4)
INTERVAL(4)
INTERVAL(4)
INTERVAL(4)
INTERVAL(4)
INTERVAL(4)INTERVAL(8)1 or 2 DINTERVALINTERVAL
INTERVAL(4)
INTERVAL(8)
INTEGER
REAL
REAL(8)
REAL(16)INTERVAL(8)
INTERVAL(8)
INTERVAL(8)
INTERVAL(8)
INTERVAL(8)
INTERVAL(8)
INTERVAL(8)INTERVAL(16)1 or 2 QINTERVALINTERVAL
INTERVAL(4)
INTERVAL(8)
INTERVAL(16)
INTEGER
REAL
REAL(8)INTERVAL(16)
INTERVAL(16)
INTERVAL(16)
INTERVAL(16)
INTERVAL(16)
INTERVAL(16)
INTERVAL(16)
TABLE 2-19 Intrinsic INTERVALTrigonometric FunctionsSine sin(a) 1 SINVDSINVSSININTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Cosine cos(a) 1 COSVDCOSVSCOSINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Tangent tan(a) 1 TANVDTANVSTANINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Arcsine arcsin(a) 1 ASINVDASINVSASININTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Arccosine arccos(a) 1 ACOSVDACOSVSACOSINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Arctangent arctan(a) 1 ATANVDATANVSATANINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Arctangent See Note 1 arctan(a/b) 2 ATAN2VDATAN2VSATAN2INTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Hyperbolic Sine sinh(a) 1 SINHVDSINHVSSINHINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Hyperbolic Cosine cosh(a) 1 COSHVDCOSHVSCOSHINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Hyperbolic Tangent tanh(a) 1 TANHVDTANHVSTANHINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)(1) arctan(a/b) = , given a = h sin
, b = h cos
, and h2 = a2 + b2.
TABLE 2-20 Other Intrinsic INTERVALMathematical FunctionsSquare Root See Note 1 exp{ln(a)/2} 1 SQRTVDSQRTVSSQRTINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Exponential exp(a) 1 EXPVDEXPVSEXPINTERVALINTERVAL(4)INTERVAL(8)INTERVAL(4)Natural logarithm ln(a) 1 LOGVDLOGVSLOGINTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)Common logarithm log(a) 1 LOG10VDLOG10VSLOG10INTERVAL(8)INTERVAL(4)INTERVAL(8)INTERVAL(4)(1) sqrt(a) is multi-valued. A proper interval enclosure must contain both the positive and negative square roots. Defining the SQRTintrinsic to beeliminates this difficulty.
TABLE 2-21 Intrinsic INTERVAL-Specific FunctionsINF inf([a, b]) = a 1 INFVDINFVSINFVQINFINTERVAL(8)INTERVAL(4)INTERVAL(16)REAL(8)REAL(4)REAL(16)SUP sup([a, b]) = b 1 SUPVDSUPVSSUPVQSUPINTERVAL(8)INTERVAL(4)INTERVAL(16)REAL(8)REAL(4)REAL(16)Width w([a, b]) = b - a 1 WIDVDWIDVSWIDVQWIDINTERVAL(8)INTERVAL(4)INTERVAL(16)REAL(8)REAL(4)REAL(16)Midpoint mid([a, b]) = (a + b)/2 1 MIDVDMIDVSMIDVQMIDINTERVAL(8)INTERVAL(4)INTERVAL(16)REAL(8)REAL(4)REAL(16)Magnitude See Note 1 max(|a|) A
1 MAGVDMAGVSMAGVQMAGINTERVAL(8)INTERVAL(4)INTERVAL(16)REAL(8)REAL(4)REAL(16)Mignitude See Note 2 min(|a|) A
1 MIGVDMIGVSMIGVQMIGINTERVAL(8)INTERVAL(4)INTERVAL(16)REAL(8)REAL(4)REAL(16)Test for empty interval true if A is empty 1 ISEMPTYVDISEMPTYVSISEMPTYVQISEMPTYINTERVAL(8)INTERVAL(4)INTERVAL(16)LOGICALLOGICALLOGICALFloor floor(A) 1 FLOORINTERVAL(8)INTERVAL(4)INTERVAL(16)INTEGERINTEGERINTEGERCeiling ceiling(A) 1 CEILINGINTERVAL(8)INTERVAL(4)INTERVAL(16)INTEGERINTEGERINTEGERPrecision precision(A) 1 PRECISIONINTERVAL(8)INTERVAL(4)INTERVAL(16)INTEGERINTEGERINTEGERRange range(A) 1 RANGEINTERVAL(8)INTERVAL(4)INTERVAL(16)INTEGERINTEGERINTEGERNumber of digits See Note 3 Maximum number of digits using Yedit descriptor1 NDIGITSINTERVALINTERVAL(4)INTERVAL(16)INTEGERINTEGERINTEGER(1) mag([a, b]) = max(|a|,|b|) (2) mig([a, b]) = min(|a|,|b|), if a > 0 or b < 0, otherwise 0 (3) Special cases: NDIGITS([-inf,+inf]) =NDIGITS([EMPTY])= 0
2.10 References
The following technical reports are available online. See the Interval Arithmetic README for the location of these files.
- G.W. Walster, E.R. Hansen, and J.D. Pryce, "Extended Real Intervals and the Topological Closure of Extended Real Relations," Technical Report, Sun Microsystems. February 2000.
- G. William Walster, "Empty Intervals," Technical Report, Sun Microsystems. April 1998.
- G. William Walster, "Closed Interval Systems," Technical Report, Sun Microsystems. August 1999.
- G. William Walster, "Literal Interval Constants," Technical Report, Sun Microsystems. August 1999.
- G. William Walster, "Widest-Need Interval Expression Evaluation," Technical Report, Sun Microsystems. August 1999.
- G. William Walster, "Compiler Support of Interval Arithmetic With Inline Code Generation and Nonstop Exception Handling," Technical Report, Sun Microsystems. February 2000.
- G. William Walster, "Finding Roots on the Edge of a Function's Domain," Technical Report, Sun Microsystems. February 2000.
- G. William Walster, "Implementing the `Simple' Closed Interval System," Technical Report, Sun Microsystems. February 2000.
- G. William Walster, "Interval Angles and the Fortran ATAN2 Intrinsic Function," Technical Report, Sun Microsystems. February 2000.
- G. William Walster, "The `Simple' Closed Interval System," Technical Report, Sun Microsystems. February 2000.
- G. William Walster, Margaret S. Bierman, "Interval Arithmetic in Forte Developer Fortran," Technical Report, Sun Microsystems. March 2000.
|
Sun Microsystems, Inc. Copyright information. All rights reserved. Feedback |
Library | Contents | Previous | Next | Index |