| Interval Arithmetic Programming Reference |
Using Interval Arithmetic With
f951.1
f95INTERVALType and Interval Arithmetic SupportInterval arithmetic is a system for computing with intervals of numbers. Because interval arithmetic always produces intervals that contain the set of all possible result values, interval algorithms have been developed to perform surprisingly difficult computations. For more information on interval applications, see the Interval Arithmetic README.
Since the inception of interval arithmetic, interval algorithms that produce narrow-width results have been developed, and the syntax and semantics for interval language support have been designed. However, relatively little progress has been made in providing commercially available and supported interval compilers. With one exception (M77 Minnesota FORTRAN 1977 Standards Version Edition 1), interval systems have been based on pre-processors, C++ classes, or Fortran 90 modules. The goals of intrinsic compiler support for interval data types in
f95are:
- Reliability
- Speed
- Ease-of-use
Interval support in the Sun WorkShop 6 release of
f95is a significant extension to Fortran.1.2
f95Interval Support Goal: Implementation QualityThe goal of intrinsic
INTERVALsupport inf95is to stimulate development of commercial interval solver libraries and applications by providing program developers with:
- Quality interval code
- Narrow-width interval results
- Rapidly executing interval code
- An easy to use interval software development environment that includes interval-specific language support and compiler features
Support and features are components of implementation quality. Throughout this book, various quality of implementation opportunities are described. Additional suggestions from users are welcome.
1.2.1 Quality Interval Code
As a consequence of evaluating any interval expression, a valid interval-supporting compiler must produce an interval that contains the set of all possible results. The requirement to contain the set of all possible results is called the containment constraint of interval arithmetic. The failure to satisfy the containment constraint is a containment failure. A silent failure (with no warning or documentation) to satisfy the interval containment constraint is a fatal error in any interval computing system. By satisfying this single constraint, intervals provide unprecedented computing quality.
Given the containment constraint is satisfied, implementation quality is determined by the location of a point in the two-dimensional plane whose axes are runtime and interval width. On both axes, small is better. How to trade runtime for interval width depends on the application. Both runtime and interval width are obvious measures of interval-system quality. Because interval width and runtime are always available, measuring the accuracy of both interval algorithms and implementation systems is no more difficult than measuring their speed.
The Sun WorkShop 6 tools for performance profiling can be used to tune interval programs. However, in
f95, no interval-specific tools exist to help isolate where an algorithm may gain unnecessary interval width. As described in Section 1.4 Code Development Tools, some intervaldbxand global program checking (GPC) support are provided. Adding additional interval-specific code development and debugging tools are quality of implementation opportunities.1.2.2 Narrow-Width Interval Results
All the normal language and compiler quality of implementation opportunities exist for intervals, including rapid execution and ease-of-use.
Valid interval implementation systems include a new additional quality of implementation opportunity: Minimize the width of computed intervals while always satisfying the containment constraint.
If an interval's width is as narrow as possible, it is said to be sharp. For a given floating-point precision, an interval result is sharp if its width is as narrow as possible.
The following can be said about the width of intervals produced by the
f95compiler:
- Individual intervals are sharp approximations of constants.
- Individual interval arithmetic operators produce sharp results.
- Intrinsic mathematical functions usually produce sharp results.
1.2.3 Rapidly Executing Interval Code
By providing compiler optimization and hardware instruction support,
INTERVALoperations are not necessarily slower than theirREALfloating-point counterparts. Inf95, the following can be said about the speed of intrinsic interval operators and mathematical functions:
- Arithmetic operations are reasonably fast.
- The speed of default
INTERVALmathematical functions is generally less than 2 times that of theirDOUBLE PRECISIONcounterparts.KIND=4intrinsic interval math functions are provided, but are not tuned for speed (unlike theirKIND=8counterparts).KIND=16mathematical functions are not provided in this release. However, otherINTERVALKIND=16functions are supported.- The following intrinsic
INTERVALarray functions are optimized for performance:1.2.4 Easy to Use Development Environment
The intrinsic
INTERVALdata type in Fortran facilitates interval code development, testing, and execution. To make interval code transparent (easy to write and read), interval syntax and semantics have been added to Fortran. User acceptance will ultimately determine which interval features are added to standard Fortran.By introducing intervals as an intrinsic data type to Fortran, all of the applicable syntax and semantics of Fortran become immediately available. Sun WorkShop 6
f95includes the following interval Fortran extensions:
INTERVALdata typesINTERVALarithmetic operations and intrinsic mathematical functions form a closed mathematical system. (This means that valid results are produced for any possible operator-operand combination, including division by zero and other indeterminate forms involving zero and infinities.)- Three classes of interval relational operators:
- Intrinsic
INTERVAL-specific operators, such as .IX. (intersection) and .IH. (interval hull)INTERVAL-specific functions, such asINF,SUP, andWIDINTERVALinput/output, including single-number input/output- Expression-context-dependent
INTERVALconstants- Mixed-mode interval expression processing
For examples and more information on these and other intrinsic interval functions, see CODE EXAMPLE 1-11 through CODE EXAMPLE 1-14 and Section 2.9.4.4 Intrinsic Functions.
Chapter 2 describes these and other interval features.
1.3 Writing Interval Code for
f95The examples in this section are designed to help new interval programmers to understand the basics and to quickly begin writing useful interval code. Modifying and experimenting with the examples is strongly recommended.
All code examples in this book are contained in the directory:
/opt/SUNWspro/examples/intervalmath/docExamplesThe name of each file is
cen-m.f95,where n is the chapter in which the example occurs, and m is the number of the example. Additional interval examples are contained in the directory:
/opt/SUNWspro/examples/intervalmath/general1.3.1 Command-Line Options
Including the following command-line macro in the
f95command line invokes recognition ofINTERVALdata types as intrinsic and controlsINTERVALexpression processing:
- Compiler support for widest-need interval expression processing is invoked by including:
-xiaor-xia=widestneed- Compiler support for strict interval expression processing is invoked by including:
-xia=strictFor intrinsic
INTERVALdata types to be recognized by the compiler, either-xiaor-xintervalmust be entered in thef95command line.All command-line options that interact with intervals are described in Section 2.3.3 Interval Command-Line Options. Widest-need and strict expression processing are described in Section 2.3 INTERVAL Arithmetic Expressions.
The simplest command-line invocation of
f95with interval support is shown in CODE EXAMPLE 1-1.1.3.2 Hello Interval World
Unless explicitly stated otherwise, all code examples are compiled using the
-xiacommand-line option. The-xiacommand-line option is required to use the interval extensions tof95.CODE EXAMPLE 1-1 is the interval equivalent of "hello world."
CODE EXAMPLE 1-1 Hello Interval World
cat ce1-1.f95PRINT *, "[2, 3] + [4, 5] = ", [2, 3] + [4, 5] ! line 1ENDmath%f95 -xia ce1-1.f95math%a.out[2, 3] + [4, 5] = [6.0,8.0]CODE EXAMPLE 1-1 uses list-directed output to print the labeled sum of the intervals [2, 3] and [4, 5].
1.3.3 Interval Declaration and Initialization
The
INTERVALdeclaration statement performs the same functions forINTERVALdata items as theREAL,INTEGER, andCOMPLEXdeclarations do for their respective data items. The defaultINTERVALkind type parameter value (KTPV) is twice the defaultINTEGERKTPV. This permits any defaultINTEGERto be exactly represented using a degenerate defaultINTERVAL. See Section 1.3.7 Default Kind Type Parameter Value (KTPV) for more information.CODE EXAMPLE 1-2 uses
CODE EXAMPLE 1-2 Hello Interval World withINTERVALvariables and initialization to perform the same operation as CODE EXAMPLE 1-1.INTERVALVariables
cat ce1-2.f95INTERVAL :: X = [2, 3], Y = [4, 5] ! Line 1PRINT *, "[2, 3] + [4, 5] = ", X+Y ! Line 2ENDmath%f95 -xia ce1-2.f95math%a.out[2, 3] + [4, 5] = [6.0,8.0]In line 1, the variables,
XandYare declared to be default typeINTERVALvariables and are initialized to [2, 3] and [4, 5], respectively. Line 2 uses list-directed output to print the labeled interval sum ofXandY.1.3.4
INTERVALInput/Output
Full support for reading and writing intervals is provided. Reading and writingINTERVALandCOMPLEXdata items are similar. Intervals use square brackets, instead of parentheses as delimiters. Because reading and interactively entering interval data can be tedious, a single-number interval format is introduced. The single-number convention is that any number not contained in brackets is interpreted as an interval whose lower and upper bounds are constructed by subtracting and adding 1 unit to the last displayed digit.
- 2.345 = [2.344, 2.346],
- 2.34500 = [2.34499, 2.34501],
- 23 = [22, 24].
- [2.34499, 2.34501] = 2.34500 + [-1, +1]uld
where [-1, +1]uld means that the interval [-1, +1] is added to the last digit of the preceding number. The subscript, uld, is a mnemonic for "unit in the last digit."
To represent a degenerate interval, a single number can be enclosed in square brackets. For example,
- [2.345] = [2.345, 2.345] = 2.345000000000.....
This convention is used both for input and representing degenerate literal
INTERVALconstants in Fortran code. Thus, type[0.1]to indicate the input value is an exact decimal number, even though 0.1 is not machine representable.For example, during input to a program,
[0.1,0.1]=[0.1]represents the point, 0.1, while using single-number input/output,0.1represents the interval
- 0.1 + [-1, +1]uld = [0, 0.2].
In
f95the input conversion process constructs a sharp interval that contains the input decimal value. If the value is machine representable, the internal machine approximation is degenerate. If the value is not machine representable, an interval having width of 1-ulp (unit-in-the-last-place of the mantissa) is constructed.
Note – A uld and an ulp are different. A uld refers to implicitly constructing an interval using the single number input/output format to add and subtract one unit to and from the last displayed digit. An ulp is the smallest possible increment or decrement that can be made to an internal machine number.
The simplest way to read and print
INTERVALdata items is with list-directed input and output.CODE EXAMPLE 1-3 is a simple tool to help users become familiar with interval arithmetic and single-number
INTERVALinput/output using list-directedREADandINTERVALinput/output is provided, as described in Section 2.9.2 Input and Output.
Caution – The interval containment constraint requires that directed rounding be used both during input and output. With single-number input followed immediately by single-number output, a decimal digit of accuracy can appear to be lost. In fact, the width of the input interval is increased by at most 1-ulp, when the input value is not machine representable. See Section 1.3.5 Single-Number Input/Output and CODE EXAMPLE 1-6.
1.3.5 Single-Number Input/Output
One of the most frustrating aspects of reading interval output is comparing interval infima and suprema to count the number of digits that agree. For example, CODE EXAMPLE 1-4 and CODE EXAMPLE 1-5 shows the interval output of a program that generates different random width
INTERVALdata.
Note – Only program output is shown in CODE EXAMPLE 1-4 and CODE EXAMPLE 1-5. The code that generates the output is included with the examples located in the/opt/SUNWspro/examples/intervalmath/docExamplesdirectory.
CODE EXAMPLE 1-4 [inf, sup] Interval Output
f95 -xia ce1-4.f95a.out5,4,05,8,05,16,0
Compare the output readability in CODE EXAMPLE 1-4 with CODE EXAMPLE 1-5.
CODE EXAMPLE 1-5 Single-Number Output.
a.out5,4,15,8,15,16,1In the single-number display format, trailing zeros are significant. See Section 2.9.2 Input and Output for more information.
Intervals can always be entered and displayed using the traditional [inf, sup] display format. In addition, a single number in square brackets denotes a point. For example, on input,
[0.1]is interpreted as the number 1/10. To guarantee containment, directed rounding is used to construct an internal approximation that is known to contain the number 1/10.
CODE EXAMPLE 1-6 Character Input with Internal Data Conversion
cat ce1-6.f951 FORMAT(" X = ? ")f95 -xia ce1-6.f95a.out1.371.444CODE EXAMPLE 1-6 notes:
- Single numbers in square brackets represent degenerate intervals.
- When a non-machine representable number is read using single-number input, conversion from decimal to binary (radix conversion) and the containment constraint force the number's interval width to be increased by 1-ulp (unit in the last place of the mantissa). When this result is displayed using single-number output, it can appear that a decimal digit of accuracy has been lost. This is not so. To echo single-number interval inputs, use character input together with internal
READstatement data conversion, as shown in CODE EXAMPLE 1-6.
Note – The empty interval is supported inf95. The empty interval can be entered as "[empty]". Infinite interval endpoints are also supported, as described in Section 2.9.2.1 External Representations and illustrated in CODE EXAMPLE 2-37.
1.3.6 Interval Statements and Expressions
The
f95compiler contains the followingINTERVAL-specific statements, expressions, and extensions:
- The
INTERVALdata type, related instructions, and statements described in TABLE 1-1 are supported.- All intrinsic functions that accept real arguments have corresponding interval versions. (It is a known error that the same is not true for integers. See Section 1.5.1.1 Integer Overflow.)
- A number of intrinsic
INTERVAL-specific functions and operators have been added, includingINTERVAL-specific relational operators and set-theoretic functions. For a complete list of intrinsicINTERVALfunctions andINTERVALoperators, see Section 2.9.3 Intrinsic INTERVAL Functions and Section 2.9.4 Mathematical Functions.1.3.7
TABLE 1-1 INTERVALSpecific Statements and ExpressionsINTERVALINTERVAL(4)INTERVAL(8)INTERVAL(16)Default INTERVALtype declarationKIND=4INTERVALKIND=8INTERVALKIND=16INTERVAL[a,b]See Note 1Literal INTERVALconstant:[a,b][a]See Note 2[a,a]INTERVAL APARAMETER A=[c,d]
Named constant:AV =exprSee Note 3Value assignment FORMAT(E,EN,ES,F,G,VE,VF,VG,VEN,VES,Y)See Note 4E,EN,ES,F,G,VE,VF,VG,VEN,VES,Yedit descriptors(1) The letters a and b are placeholders for literal decimal constants, such as 0.1and0.2. (2) A single decimal constant contained in square brackets denotes a degenerateINTERVALconstant. The same convention is used in input/output. (3) Letexprstand for any Fortran arithmetic expression, whether or not it contains items of typeINTERVAL. An assignment statement,V=expr, evaluates the expression,expr, and assigns the resulting value toV. Mixed-modeINTERVALexpressions are not permitted under the-xia=strictcommand line option. Under the-xiaor-xia=widestneedoption, mixed-mode expressions are correctly evaluated using widest-need expression processing. Before expression evaluation under widest-need, all integer and floating-point data items are promoted to containing intervals with the largest KTPV found anywhere in the expression, including,V. For details, see Section 2.3.2 Value Assignment. (4) Interval input/output support is designed to provide flexibility, readability, and ease of code development. The most important new edit descriptor isY, which is used to read and display intervals using the single-number interval format. For a complete description of all edit descriptors that can process intervals, see Section 2.9.2 Input and Output.
Default Kind Type Parameter Value (KTPV)In
f95the defaultINTEGERKTPV isKIND(0)= 4. To represent any defaultINTEGERwith a degenerate defaultINTERVALrequires the defaultINTERVALKTPV,KIND([0]), to be2*KIND(0)= 8. Choosing 8 for the defaultINTERVALKTPV is also done because:
- Intervals are often used to perform numerically intense computations, as have been performed on CDC and Cray machines.
- When evaluating a single arithmetic expression, the width of intervals necessarily grows because of accumulated rounding errors, dependence, and cancellation. Extra precision can help to reduce the effect of accumulated rounding errors.
1.3.8 Value Assignment
V=exprThe
INTERVALassignment statement assigns the value of an interval expression, denoted by the placeholderexpr, to anINTERVALvariable, array element, or array,V. The syntax is:
V=exprwhere
Vmust have anINTERVALtype, andexprdenotes any non-COMPLEXnumeric expression. Under widest-need expression processing, the expressionexprneed not be anINTERVALexpression. Under strict expression processing,exprmust be anINTERVALexpression with the same KTPV asV.1.3.9 Mixed-Type Expression Evaluation
Gracefully handling mixed-type
INTERVALexpressions is an important ease-of-use feature, because it facilitates writing transparent (easy to understand) mathematical expressions.Mixed-type
INTERVALexpressions are supported to make writing and reading interval code no more difficult than it is forREALcode. The interval containment constraint is satisfied in mixed-mode expressions using either widest-need or strict expression processing.1.3.9.1 Widest-Need and Strict Expression Processing
Computing narrow-width interval results is facilitated if the width of
CODE EXAMPLE 1-7 Mixed Precision with Widest-NeedINTERVALconstants is dynamically defined by expression context, as described in Section 2.3 INTERVAL Arithmetic Expressions. In mixed-KTPV expressions, shown in CODE EXAMPLE 1-7, dynamically increasing the KTPV ofINTERVALvariables can also decrease the width ofINTERVALexpression results.
math%cat ce1-7.f95INTERVAL(4) :: X = [1, 2], Y = [3, 4]INTERVAL :: Z1, Z2! Widest-need CodeZ1 = X*Y ! Line 3! Equivalent Strict CodeZ2 = INTERVAL(X, KIND=8)*INTERVAL(Y, KIND=8) ! Line 4IF (Z1 .SEQ. Z2) PRINT *, 'Check.'ENDmath%f95 -xia ce1-7.f95math%a.outCheck.In line 3, KTPVmax =
KIND(Z)=8. This value is used to promote the KTPV ofXandYto 8 before computing their product and storing the result inZ1.These steps are shown explicitly in the equivalent strict code in line 4.
The process of scanning a statement to determine the maximum KTPV and performing the necessary promotions, is called widest-need expression processing, see Section 2.3 INTERVAL Arithmetic Expressions.
For syntax and semantics of the intrinsic
INTERVALconstructor functions, see Section 2.8 Extending Intrinsic INTERVAL Operators.1.3.9.2 Mixed-Mode (Type and KTPV) Expressions
If the widest-need principle is used with both KTPVs and data types, mixed-mode (type and KTPV)
CODE EXAMPLE 1-8 Mixed TypesINTERVALexpressions can be safely and predictably evaluated. For example, in CODE EXAMPLE 1-8, the expression forY1in line 3 is an interval expression, becauseXandY1areINTERVALvariables.
with Widest-Need
cat ce1-8.f95INTERVAL(16) :: X = [0.1, 0.3]INTERVAL(4) :: Y1, Y2! Widest-need codeY1 = X + 0.1 ! Line 3! Equivalent strict codeY2 = INTERVAL(X + [0.1_16], KIND=4) ! Line 4IF (Y1 == Y2) PRINT *, "Check"ENDmath%f95 -xia ce1-8.f95math%a.outCheckTo guarantee containment, a containing interval must be used in place of a real approximation to the constant 0.1. However, KTPVmax = 16, because
KIND(X)=16. Therefore, theINTERVALconstant [0.1_16], a sharp KTPV = 16 interval containing the exact value, 1/10, is used to updateX. Finally, the result is converted to a KTPV = 4 containing interval and assigned toY1. Line 4 contains the equivalent strict code. Under strict expression processing, neither mixed-type nor mixed-KTPV expressions are permitted.The logical steps in widest-need expression processing are:
1. Scan the entire statement, including the left-hand side, for anyINTERVALdata items.
- The presence of any
INTERVALconstants, variables, or intrinsic functions, makes the expression's typeINTERVAL.2. Scan theINTERVALexpressions for KTPVmax , based on the KTPV of eachINTERVAL,REAL,INTEGER, constant, or variable.
Note – Integers are converted to intervals with twice their KTPV so all integer values can be exactly represented.
3. Promote all variables and constants to intervals with KTPVmax.4. Evaluate the expression.5. Convert the result to a lower KTPV if needed to match the left-hand side's KTPV.6. Assign the resulting value to the left-hand side.These steps guarantee that mixed-mode
INTERVALexpression processing satisfies the containment constraint and efficiently produces reasonably narrow interval results.Mixed-mode
INTERVALexpression evaluation using widest-need expression processing is supported by default with the-xiacommand-line flag. Using -xia=stricteliminates any automatic type conversions to intervals and any automatic KTPV increases ofINTERVALvariables. In strict mode, all interval type and precision conversions must be explicitly coded.1.3.10 Arithmetic Expressions
Writing arithmetic expressions that contain
CODE EXAMPLE 1-9 SimpleINTERVALdata items is simple and straightforward. Except forINTERVALliteral constants and intrinsicINTERVAL-specific functions,INTERVALexpressions look likeREALarithmetic expressions. In particular, with widest-need expression processing,REALandINTEGERvariables and literal constants can be freely used anywhere in anINTERVALexpression, such as in CODE EXAMPLE 1-9.INTERVALExpression Example
cat ce1-9.f95INTEGER :: N = 3REAL :: A = 5.0INTERVAL :: XX = 0.1*A/N ! Line 5PRINT *, "0.1*A/N = ", XENDmath%f95 -xia ce1-9.f95math%a.out0.1*A/N = [0.16666666666666662,0.16666666666666672]Because
X, the variable to which the assignment is made in line 5, is anINTERVAL, the following steps are taken before evaluating the expression0.1*A/N:
- The literal constant 0.1 is converted to the default
INTERVALvariable containing the degenerate interval[0.1].- The
REALvariableAis converted to the degenerate interval[5].- The
INTEGERvariableNis converted to the degenerate interval[3].The expression [0.1] × [5]/[3] is evaluated using interval arithmetic. The above steps are part of widest-need expression processing, which is required to satisfy the containment constraint when evaluating mixed-mode
INTERVALexpressions. See Section 1.3.9 Mixed-Type Expression Evaluation.An
INTERVALassignment statement must satisfy one requirement: the variable to which the assignment is made must be anINTERVALvariable, array element, or array. For more information on the widest-need processing mode, see Section 2.3.1 Mixed-Mode INTERVAL Expressions.Because the interval system implemented in Sun WorkShop 6
f95is closed, if anyINTERVALexpression fails to produce a valid interval result, it is a compiler error that should be reported. See Section 1.4 Code Development Tools for information on how to report a suspected error and Section 1.5.1 Known Containment Failures for a list of known errors.
Note – Not all mathematically equivalentINTERVALexpressions produce intervals having the same width. Additionally, it is often not possible to compute a sharp result by simply evaluating a singleINTERVALexpression. In general, interval result width depends on the value ofINTERVALarguments and the form of the expression.
1.3.11 Interval Order Relations
Ordering intervals is more complicated than ordering points. Testing whether 2 is less than 3 is unambiguous. With intervals, while the interval
[2,3]is certainly less than the interval[4,5], what should be said about[2,3]and[3,4]?Three different classes of
INTERVALrelational operators are implemented:
- certainly
- possibly
- set
For a certainly-relation to be true, every element of the operand intervals must satisfy the relation. A possibly-relation is true if it is satisfied by any elements of the operand intervals. The set-relations treat intervals as sets. The three classes of
INTERVALrelational operators converge to the normal relational operators on points if both operand intervals are degenerate.To distinguish the three operator classes, the normal two-letter Fortran relation mnemonics are prefixed with the letters
C,P, orS. Inf95the set operators.SEQ.and.SNE.are the only operators for which the point defaults (.EQ.or==and.NE.or/=) are supported. In all other cases, the relational operator class must be explicitly identified, as for example in:
.CLT.certainly less than.PLT.possibly less than.SLT.set less thanSee Section 2.4 Intrinsic Operators for the syntax and semantics of all
INTERVALoperators.The following program demonstrates the use of a set-equality test.
CODE EXAMPLE 1-10 Set-Equality Test
cat ce1-10.f95INTERVAL :: X = [2, 3], Y = [4, 5] ! Line 1IF(X+Y .SEQ. [6, 8]) PRINT *, "Check." ! Line 2ENDmath%f95 -xia ce1-10.f95math%a.outCheck.Line 2 uses the set-equality test to verify that
X+Yis equal to the interval [6, 8].IF(X+Y == [6, 8]) PRINT *, "Check." ! line 2UseCODE EXAMPLE 1-11 and CODE EXAMPLE 1-12 to explore the result of
INTERVAL-specific relational operators.
CODE EXAMPLE 1-11 Interval Relational Operators
cat ce1-11.f95f95 -xia ce1-11.f95a.out[2] [3]2 3CODE EXAMPLE 1-12 demonstrates the use of the
INTERVAL-specific operators listed in TABLE 1-2.
TABLE 1-2 Interval-Specific Operators Interval Hull 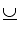
Intersection 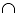
Disjoint 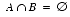
Element 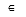
Interior See Section 2.7.3 Interior: (X .INT. Y). Proper Subset 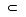
Proper Superset 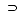
Subset 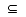
Superset 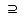
CODE EXAMPLE 1-12 Set Operators
cat ce1-12.f951 FORMAT(" X, Y = ? ")f95 -xia ce1-12.f95a.out[1] [2][1,2][1,3]1.3.12 Intrinsic
INTERVAL-Specific FunctionsA variety of intrinsic
INTERVAL-specific functions are provided. See Section 2.9.4.4 Intrinsic Functions. Use CODE EXAMPLE 1-13 to explore how intrinsicINTERVALfunctions behave.
CODE EXAMPLE 1-13 Intrinsic INTERVAL-Specific Functions
cat ce1-13.f951 FORMAT(" X = ?")f95 -xia ce1-13.f95a.out[1.23456,1.234567890][1,10]1.3.13 Interval Versions of Standard Intrinsic Functions
Every Fortran intrinsic function that accepts
REALarguments has an interval version. See Section 2.9.4.4 Intrinsic Functions. Use CODE EXAMPLE 1-14 to explore how some intrinsic functions behave.
CODE EXAMPLE 1-14 Interval Versions of Standard Intrinsic Functions
cat ce1-14.f951 FORMAT(" X = ?")f95 -xia ce1-14.f95a.out[1.1,1.2][-0.5,0.5]1.4 Code Development Tools
Information on interval code development tools is available online. See the Interval Arithmetic README for a list of interval web sites and other online resources.
To report a suspected interval error, send email to
sun-dp-comments@Sun.COMInclude the following text in the Subject line of the email message:
WORKSHOP "6.0mm/dd/yy" Intervalwhere mm/dd/yy is the month, day, and year.
1.4.1 Debugging Support
In Sun WorkShop 6, interval data types are supported by dbx to the following extent:
- The values of individual
INTERVALvariables can be printed using the- The value of all
INTERVALvariables can be printed using thedumpcommand.- New values can be assigned to
INTERVALvariables using theassigncommand.- Printing the value of
INTERVALexpressions is not supported.- There is no provision to visualize
INTERVALdata arrays.- All generic functionality that is not data type specific should work.
For additional details on
dbxfunctionality, see Debugging a Program With dbx.1.4.2 Global Program Checking
Global program checking (GPC) in Sun WorkShop 6 Fortran 95 detects one interval-specific error:
CODE EXAMPLE 1-15INTERVALtype mismatches in user-supplied routine calls.INTERVALType Mismatch
cat ce1-15.f95INTERVAL XX = [-1.0,+2.9]PRINT *,XCALL SUB(X)ENDSUBROUTINE SUB(Y)INTEGER Y(2)PRINT *,YENDmath%f95 -xia ce1-15.f95 -Xlist--- See ce1-15.lst ---Global Call-Chain Considerata===============================1) <503> At line 4, MainPgm() calls SUB(fileline 6):MainPgm() sends argument 1 as type "Interval(16),"but SUB() expects type "Integer(4)"2) <507> At line 4, MainPgm() calls SUB(fileline 6):MainPgm() sends argument 1 as a "Scalar,"but SUB() expects a "1-D Array"1.4.3 Interval Functionality Provided in Sun Fortran Libraries
The following libraries contain intrinsic
INTERVALroutines.
TABLE 1-3 Interval Libraries intrinsic INTERVALarray functionslibifaiNone intrinsic INTERVALlibrarylibsunimathNone
1.4.4 Porting Code and Binary Files
There is limited legacy interval Fortran code with which to contend. Until language syntax and semantics are standardized, different providers of interval compiler support will inevitably diverge. The standardization process will be facilitated if users provide feedback regarding the most favored
INTERVALsyntax and semantics. Comments can be sent to the email alias listed in the Interval Arithmetic README.The representation of intervals in binary files will change as compilers supporting narrower interval systems are made available.
1.4.5 Parallelization
In this release, the
-autoparcompiler option has no effect on loops containing interval arithmetic operations. These loops are not automatically parallelized. The-explicitparcompiler option must be used to parallelize loops marked with explicit parallelization directives.1.5 Error Detection
The following code samples list interval-specific error messages. Each code sample includes the error message and the sample code that produced the error.
CODE EXAMPLE 1-16 Invalid Endpoints
CODE EXAMPLE 1-17 Equivalence of Intervals and Non-Intervals
cat ce1-16.f95INTERVAL :: I = [2., 1.]ENDmath%f95 -xia ce1-16.f95INTERVAL :: I = [2., 1.]^"ce1-14.f95", Line = 1, Column = 24: ERROR: The left endpoint of the interval constant must be less than or equal to the right endpoint.f90: COMPILE TIME 0.150000 SECONDSf90: MAXIMUM FIELD LENGTH 4117346 DECIMAL WORDSf90: 2 SOURCE LINESf90: 1 ERRORS, 0 WARNINGS, 0 OTHER MESSAGES, 0 ANSI
CODE EXAMPLE 1-18 Equivalence of
cat ce1-17.f95INTERVAL :: IREAL :: REQUIVALENCE (I, R)ENDmath%f95 -xia ce1-17.f95EQUIVALENCE (I, R)^"ce1-15.f95", Line = 3, Column = 14: ERROR: Equivalence of INTERVAL object "I" and REAL object "R" is not allowed.f90: COMPILE TIME 0.160000 SECONDSf90: MAXIMUM FIELD LENGTH 4117346 DECIMAL WORDSf90: 4 SOURCE LINESf90: 1 ERRORS, 0 WARNINGS, 0 OTHER MESSAGES, 0 ANSIINTERVALObjects with Different KTPVs
CODE EXAMPLE 1-19 Assigning a
cat ce1-18.f95INTERVAL(4) :: I1INTERVAL(8) :: I2EQUIVALENCE (I1, I2)ENDmath%f95 -xia ce1-18.f95EQUIVALENCE (I1, I2)^"ce1-16.f95", Line = 3, Column = 14: ERROR: Equivalence of the interval objects "I1" and "I2" with the different kind type parameters is not allowed.f90: COMPILE TIME 0.190000 SECONDSf90: MAXIMUM FIELD LENGTH 4117346 DECIMAL WORDSf90: 4 SOURCE LINESf90: 1 ERRORS, 0 WARNINGS, 0 OTHER MESSAGES, 0 ANSIREALExpression to anINTERVALVariable in Strict Mode
CODE EXAMPLE 1-20 Assigning an
cat ce1-19.f95INTERVAL :: XREAL :: RX = RENDmath%f95 -xia=strict ce1-19.f95X = R^"ce1-17.f95", Line = 3, Column = 3: ERROR: Assignment of a REAL expression to a INTERVAL variable is not allowed.f90: COMPILE TIME 0.350000 SECONDSf90: MAXIMUM FIELD LENGTH 4117346 DECIMAL WORDSf90: 4 SOURCE LINESf90: 1 ERRORS, 0 WARNINGS, 0 OTHER MESSAGES, 0 ANSIINTERVALExpression toINTERVALVariable in Strict Mode
cat ce1-20.f95INTERVAL :: XINTERVAL(16) :: yX = YENDmath%f95 -xia=strict ce1-20.f95X = Y^"ce1-18.f95", Line = 3, Column = 3: ERROR: Assignment of an interval expression to an interval variable is not allowed when they have different kind type parameter values.f90: COMPILE TIME 0.170000 SECONDSf90: MAXIMUM FIELD LENGTH 4117346 DECIMAL WORDSf90: 4 SOURCE LINESf90: 1 ERRORS, 0 WARNINGS, 0 OTHER MESSAGES, 0 ANSI1.5.1 Known Containment Failures
Whenever an interval containment failure can occur, a compile-time warning should be issued. An integer expression outside the scope of widest-need expression processing is the only known situation in which such a warning is necessary.
1.5.1.1 Integer Overflow
Numerical inaccuracies are normally associated with
REALrather thanINTEGERexpressions. In one respect,INTEGERexpressions are more dangerous thanREALexpressions. WhenREALexpressions overflow, an exception is raised, and an IEEE infinity is generated. The exception is a warning that overflow has occurred. Infinities tend to propagate in floating-point computations, thereby alerting users of a potential problem. It is also possible to trap on overflow.When
INTEGERexpressions overflow, they silently wrap around to some possibly-opposite-signed value. Moreover, the only practical way to detect integer overflow is to perform the inverse operation and test for equality on every integer operation. Integer constant expressions are safe because they are evaluated during compilation where overflow is detected and signalled with a warning message.The following example shows what can happen if the scope of widest-need expression processing is not extended to all intrinsic
CODE EXAMPLE 1-21INTEGERoperations and functions, including the ** operation with anINTEGERexponent.INTEGEROverflow Containment Failure
cat ce1-21.f95INTERVAL :: X = [2], Y = [2]INTEGER :: I = HUGE(0)X = X**(I+1)Y = Y*(Y**I)IF(X .DJ. Y) PRINT *, "X and Y are disjoint."ENDmath%f95 -xia ce1-21.f95math%a.outX and Y are disjoint.This code demonstrates a silent containment failure. It is a known error because the scope of widest need expression processing does not presently extend to the integer exponent of the ** operation. For information on the power operator, see Section 2.5 Power Operators X**N and X**Y.
Caution – This error has not been fixed in the Sun WorkShop 6 Fortran 95 release, and no warning messages are issued.
|
Sun Microsystems, Inc. Copyright information. All rights reserved. Feedback |
Library | Contents | Previous | Next | Index |