| ���ͷ������� |
��Ͽ D
��ư�������黻�ˤĤ���
�� - ������Ͽ�ϡ�1991 ǯ 3 ��ȯ�Ԥ� "Computing Surveys" �˷Ǻܤ��줿 "Every Computer Scientist Should Know About Floating-Point Arithmetic" �� (David Goldberg��) ����Խ����������ͭ���� Association for Computing Machinery �� (Copyright 1991) �ε��ĤΤ�Ȥˡ��������ʤ�������ΤǤ���
����
��ư�������黻�ϡ���������������Ȥ��Ƽ�������뤳�Ȥ�����ޤ�������ԥ塼�������ƥ�������ˤϡ���ư�������黻��������Ȥ�����¸�ߤ�������ͤ���С�����ǧ���ˤ�¿�������¤ȤΤ��줬����褦�Ǥ������Ȥ��С��ۤȤ�ɤΥ���ԥ塼������ˡ���ư�������Υǡ����������Ѥ���Ƥ��ޤ����ޤ� PC ���饹���ѡ�����ԥ塼���˻��ޤǤ����륳��ԥ塼������ư��������������졼�������Ѥ���Ƥ��ޤ����������ư���������르�ꥺ���ѥ��뤹�뤿��ˡ�����ѥ��餬�ƤӽФ���뤳�Ȥ��褯����ޤ������¤ˤϡ������С��ե����ʤɤ���ư�������㳰���б����Ƥ��ʤ����ڥ졼�ƥ������ƥ�ʤɳ�̵�Ǥ���Ȥ�����ޤ���������Ͽ�Ǥϡ�����ԥ塼�������ƥ���߷�ô���Ԥ��Ф���ľ��Ū�ʱƶ���Ϳ������ư�������Τ��ޤ��ޤ�¦�̤ˤĤ����������ޤ�������Ū�ˤϡ���ư������ɽ�����طʡ��ݤ������IEEE ��ư������ɸ��ˤĤ����������ޤ����Ǹ�˥���ԥ塼���߷Ԥ���ư��������ɤΤ褦�˥��ݡ��ȤǤ��뤫������Ĥ��Ҳ𤷤ޤ���
���ƥ���/���֥������ȵ��һ� (�켡 ) C.0 [����ԥ塼�������ƥ������] ������ �� ̿��åȤ��߷���D.3.4 [�ץ�����ߥ���] ���ץ����å� �� ����ѥ�������Ŭ����G.1.0 [���Ͳ���] ������ �� ����ԥ塼���黻�����顼���������ͥ��르�ꥺ�� (�� )
D.2.1 [���եȥ��������˥����] ����/���� �� ������D.3.4 [�ץ�����ߥ���] ����������������� �� ���ޥ�ƥ�������D.4.1 [���ڥ졼�ƥ������ƥ�] ���ץ��������� �� Ʊ����
����¾�Υ�����ɤ�ɽ�����������������㳰����ư����������ư������ɸ�ࡢ�ʳ�Ū��������ե������ݸ�塢NaN�������С��ե��������и������ݤ�������ݤ�⡼�ɡ�ulp����������ե���
�Ϥ����
����ԥ塼�������ƥ���߷�Ȥ�ʤ���ǡ���ư�������黻�˴ؤ������ɬ�פˤʤ뤳�Ȥ��褯����ޤ������������¤ˤϡ���ư�������黻�˴ؤ���ܤ��������ϰճ��ʤۤɾ��ʤ���ΤǤ�����������ä������ʤ����Ҥ�1�ĤǤ��� "Floating-Point Computation" (Pat Sterbenz ��) �⡢���Ǥ��Ѵ��ˤʤäƤ��ޤ���������Ͽ�Ǥϡ�����ԥ塼�������ƥ���߷פ��礭�����������ư�������黻�γ�¦�̤ˤĤ��ƾܤ����������ޤ���������Ͽ���礭�� 3 ����ʬ�����ޤ����ִݤ�����������Ǥϡ���§�黻�δ���Ū�����˳Ƽ�δݤ�⡼�ɤ�Ŭ�Ѥ������αƶ��ˤĤ����������ޤ����ޤ� ulp �����и����Ȥ��� 2 ����δݤ������¬����ˡ�˴ؤ����طʾ�����ޤ���2 ���Ǥϡ�¿���Υϡ��ɥ������٥�����ƼҤˤ�äƵ�®�������Ǻ��Ѥ���ĤĤ��� IEEE ��ư������ɸ��ˤĤ����������ޤ���IEEE ɸ��ˤϡ�����Ū�ʱ黻�˴ؤ���ݤ����ˡ���������Ƥ��ޤ���IEEE ɸ��ˤĤ��Ƥϡ��ִݤ�������˼�������ˤ�ȤŤ����������ޤ�������Ū�ˤ�̿��åȤ��߷ס���Ŭ������ѥ��顢������㳰�����ˤĤ����������ޤ���
������Ͽ����ư�������ˤĤ�����������Ȥ��ϡ�ɬ�������������������Ǥ���Ȥ�����������ͳ��ʻ���Ƽ����Ƥ���ޤ�������ϡ�������ͳ�˴ؤ����������Τ���ñ��ʷ������ǤϺѤޤ����Ȥ��Ǥ��ʤ���礬�褯���뤫��Ǥ����ޤ������μ�ݤ�ľ��Ū�ˤϴط��Τʤ����ƤˤĤ��Ƥϡ־ܺ١פȤ��������Ω���Ƽ����Ƥ���ޤ����־ܺ١פ��ɤ����Ф��Ƥ⤫�ޤ��ޤ��ޤ���������Ͽ�ˤ��äˡ������˴ؤ���־����פ���¿���Ҳ𤷤Ƥ���ޤ����־����פν����βս�Ϣ��ε�����դ���ɽ�路�ޤ����ޤ��־����פ��ά�������ϡ����ε����������ʸ��ľ��˼����ޤ���
�ݤ����
¿���μ¿���ͭ�¸ĤΥӥåȤ����̵�¤˰��̤��Ƥ����ˤϡ�����ͤ�ɽ����ɬ�פˤʤ�ޤ��������ˤ�̵�¤ο�������ޤ������ץ��������Ǥ��̾�����黻�η�̤� 32 �ӥåȤ��Ȥ˳�Ǽ����ޤ���������Ǥ�դθ�����ӥåȤǡ��¿���ȼ���黻��Ԥ����ϡ��ɤ�ۤ�¿���ΥӥåȤ���Ѥ��Ƥ⡢��̤��ͤ����Τˤ�ɽ���Ǥ��ʤ��ʤäƤ��ޤ����������äơ���ư�������黻�η�̤ˡ��ݤ�����ä��뤳�Ȥˤ�äơ�ͭ�¤��ϰ���˼����ɽ�����ʤ���Фʤ�ޤ����δݤ����ΤȤ�������������ϡ���ư�������黻�����ڤ�Υ�����ȤΤǤ��ʤ������ȸ����ޤ����ݤ������¬����ˡ�ˤĤ��Ƥϡ������и����� ulp���Ȥ��Ƥ���������
���⤽�⡢�̾����ư�������黻�Ǵݤ������������뤳�Ȥ��Ǥ��ʤ��Τ��Ȥ���С�����Ū�ʱ黻������¿���δݤ�������Ф뤳�Ȥ˲������꤬����ΤǤ��礦�������κ���Ū�ʵ��䤳�������ι�ǰ������פ�����ˤۤ��ʤ�ޤ������ݸ����Ǥ��ݸ��ˤĤ����������Ƥ��ޤ����ݸ�����ݤ��뤳�Ȥˤ�ꡢ2 �Ĥζᤤ�ͤ�����Ȥ��θ������㸺���뤳�Ȥ��Ǥ��ޤ����ݸ������衢IBM �� 1968 ǯ�ˡ�System/360 �������ƥ�����������٥ե����ޥåȤȤ����ݸ��Ѥη���ɲä��� (ñ���٥ե����ޥåȤˤϤ��Ǥ��ݸ�夬���ꤵ��Ƥ��ޤ���) ���Ȥ��б����ơ���¸�����ޥ��������������Ȥ����ä����ǽ��뤵���褦�ˤʤ�ޤ������ݸ��θ��Ѥ���� 2 �ľҲ𤷤ޤ���
IEEE ɸ��λ��ͤϡ�ñ�ʤ��ݸ���ɬ�������᤹������Τ�ΤǤϤ���ޤ���§�黻�Τۤ���ʿ�������Υ��르�ꥺ�ब�Ѱդ��졢�ƥ��르�ꥺ���Ʊ����̤������Ǥ��������ɬ�פˤʤ�ޤ����������äơ�����ޥ����̤Υޥ���˥ץ�������ܿ��������Ǥ⡢ξ���Υޥ���Ǥ� IEEE ɸ�ब���ݡ��Ȥ���Ƥ���С����ܱ黻�ˤ��ƥӥåȤ��Ȥˡ��ޤä���Ʊ����̤���������뤳�Ȥˤʤ�ޤ��������Τʴݤ������ˤϡ��������Τʻ��ͤˤ�ȤŤ����̤�����ޤ���
��ư�������ե����ޥå�
����ޤǤˤ⡢�¿���ɽ�����뤵�ޤ��ޤʷ�������Ƥ���Ƥ��ޤ��������Τ����Ǥ����Ū�ʷ�������ư������ɽ�� 1�Ǥ�����ư������ɽ���Ǥϡ���� �� (�Ĥͤ˶����Ȥ��ޤ�) ������ p ����Ѥ��ޤ����� = 10 �ǡ�p = 3 �Ȥ���ȡ�0.1 �Ȥ����ͤ�1.00 × 10-1 ��ɽ�路�ޤ����ޤ� �� = 2 �ǡ�p = 24 �ξ�硢�������� 0.1 �����Τ�ɽ�����뤳�ȤϤǤ��ޤ������褽 1.10011001100110011001101 × 2-4 �Ȥʤ�ޤ������̤ˡ���ư���������� �� d.dd... d × ��e ��ɽ�蘆��ޤ� (������ d.dd... d �ϡ�ͭ�շ��2�ȸƤФ졢����� p �Ȥʤ�ޤ�)����������Τ˸����ȡ�� d0 . d1 d2 � dp-1 × ��e �ϡ����ο���ɽ�路�ޤ���
(1)
��ư���������Ȥ����Ѹ�ϡ��嵭�Τ褦�ʷ�����ɽ���Ǥ���¿��Τ��Ȥ�ؤ��ޤ�����ư������ɽ���Ǥϡ�������ƻؿ� emax �ȺǾ����ƻؿ� emin �Ȥ��� 2 �ĤΥѥ�������Ѥ��ޤ���ͭ�շ夬��p �Ĥǡ����ƻؿ��� emax - emin + 1 �Ȥ���С���ư���������ϼ��Τ褦�˥����ǥ��Ǥ��ޤ���
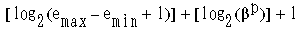
�Ǹ�� + 1 �����ӥåȤ�ɽ�路�ޤ��������ǥ����ǥ����Τ�Τϡ����פǤϤ���ޤ��¿�����ư���������Ȥ��Ƥ����Τ�ɽ������ʤ���ͳ�� 2 �Ĥ���ޤ����Ǥ����Ū�ʥ������Ͼ������� 0.1 ����Ǥ��������ͭ�¤� 10 �ʾ��������Ȥ���ɽ������ޤ�����2 �ʿ��Ǥ�̵�¤�ȿ��ɽ���ˤʤ�ޤ����������äơ���= 2 �ξ�硢0.1 �Ȥ������ͤ����Τˤ� 2 �Ĥ���ư���������δ֤�¸�ߤ��Ƥ��ꡢ��������ͤǤ���������ɽ���Ǥ��ʤ����Ȥˤʤ�ޤ���
�ޤ����̤ξ����Ȥ��Ƽ¿���ͭ���ϰϤ�Ķ�����硢���ʤ�������ͤ��� ×
�ʾ塢���뤤�� 1.0 ×
�ʲ��ˤʤäƤ��륱�������ͤ��ޤ���������Ͽ�Ǥϡ��ǽ������˸¤äư����ޤ����ʤ���ͭ���ϰϤ�Ķ������ͤˤĤ��Ƥϡ���̵������������ ���������������γƹ���������ޤ���
��ư������ɽ���ϡ�ɬ�������դ�ɽ���ˤϤʤ�ޤ���
�㤨�С�0.01 × 101 �� 1.00 × 10-1 �Ϥ������ 0.1 ��ɽ�路�ޤ�����Է夬�����ʳ� (�嵭�θ��� (1) �� d0 �� 0 �ξ��) �Ǥ���С�ɽ���ϡ�����������Ƥ���פȸ����ޤ�����ư�������� 1.00 × 10-1 ������������ޤ�����0.01 × 101 ������������ޤ���=2��p = 3��emin = -1��emax = 2 �ξ�硢�� D-1 �˼����Ȥ��ꡢ�� 16 �Ĥ���������ư����������¸�ߤ��ޤ����ޤ�������ͭ�շ夬 1.00 �Ȥʤ��ͤ�ɽ�路�ޤ�����ư������ɽ��������������ȡ���դ�ɽ���������ޤ������������������¤ˤ�äƥ�����ɽ�����뤳�Ȥ��Ǥ��ʤ��ʤ�ޤ���������ɽ���������Ū����ˡ�Ȥ��ơ�1.0 ×����Ѥ��ޤ�������ˤ�ꡢ����μ¿���ɽ�魯�ֹ椬��ư������ɽ���μ�����������б����Ƥ���Ȥ������¤��ݻ�����ޤ�3���ؿ��� k �ӥåȥե�����ɤ˳�Ǽ����ȡ�1 �ӥå�ʬ�� 0 ��ɽ�魯�����ͽ��ɬ�פ�����Τǡ�2k - 1 ���ͤ������ؿ��ѤȤ��Ƴ��ݤ���뤳�Ȥˤʤ�ޤ���
�ʤ�����ư���������� × ��ɽ���ΰ����Ȥ��ƻ��Ѥ�����Τǡ���ư�������ξ軻����Ȥϰۤʤ�ޤ���× ����ΰ�̣�ϡ�ʸ̮�����ñȽ�Ǥ��뤳�Ȥ��Ǥ��ޤ���
�� D-1 �������� ��= 2��p = 3��emin = -1��emax = 2
�㤨�С�(2.5 × 10-3) × (4.0 × 102) �Ȥ������Ǥϡ���ư�������ξ軻�� 1 ������Ԥ��Ȥ�����̣�ˤʤ�ޤ���
������� ulp
��ư�������黻�Ǥ����衢�ݤ�������뤳�Ȥ��Ǥ��ʤ��Τǡ����θ�����¬�ꤹ����ˡ���Ω���Ƥ������Ȥ����פǤ������� ��=10��p = 3�Ȥ�����ư�������ե����ޥåȤ����ͤ��Ƥߤޤ� (������Ͽ�Ǥϡ�Ʊ�������Ѥ��ޤ�)����ư�������黻�η�̤� 3.12 × 10-2 �ξ��ǡ����̵�¤����٤��Ф��Ʒ������ 0.0314 �ˤʤꡢ�ǽ���� 2 ��˥åȤθ��������뤳�Ȥ��狼��ޤ���Ʊ���褦�ˡ��¿� 0.0314159 �� 3.14 × 10-2 �Ȥ���ɽ�魯�ȡ��ǽ���θ����� 0.159 �Ȥʤ�ޤ������̤���ư�������� d.d...d × ��e ����Ѥ��� z ��ɽ�路����硢�ǽ���θ����ϡ�d.d...d - (z/��e)�æ�p-1 ��˥åȤȤʤ�ޤ�4 5��ulp�Ȥ����Ѹ�ϡ�"units in the last place" (�ǽ���Υ�˥å�) ��ά������ΤǤ������η�̤������Τ��ͤ˥���ζᤤ��ư�������ͤȤʤ��硢0.5 ulp����������뤳�Ȥˤʤ�ޤ�����ư�������ͤȼ¿����ͤθ�����ɽ�魯���ˡ����и����ζ���ͤ���뤳�Ȥ�Ǥ��ޤ������и����Ȥϡ���ư���������ȼ¿��κ���¿��ͤdz�ä���̤Τ��ȤǤ����㤨�С�3.14159 �� 3.14 × 100 �ˤ�äƶ��ɽ�������������и����� 0.00159/3.14159=0.0005 �Ȥʤ�ޤ���
0.5 ulp �������������и�����������硢�ºݤ��ͤ˺Ǥ�ᤤ�ͤ� d.dd...dd × ��e ��ɽ�魯�ȡ�0.00...00�¡�× ��e ��θ������Ф뤳�Ȥ�����ޤ� (������ �¡�� ��/2 �η��ɽ�路����ư����������ͭ�շ�θ����� p ��˥åȡ��ޤ�������ͭ�շ� p ��˥åȤϥ����ˤʤ�ޤ�)�����θ����� ((��/2)��-p) × ��e �Ǥ���d.dd...dd × ��e �η����ο������и����Ϥ��٤�Ʊ���ˤʤ�������ͤϤ��٤Ʀ�e ���� �� × ��e ���ϰϤˤ���Τǡ����и����� ((��/2)��-p) × ��e/��e �� ((��/2)��-p) × ��e/��e+1 ���ϰϤ�¸�ߤ��ޤ���
(2)
�äˡ�0.5 ulp �������������и����ϡ��� ���Ȥ��Ʋ��ѤȤʤ�ޤ������η����Τ��Ȥ�֥�֥�פȸ����ޤ�����= (��/2)��-p ��弰 (2) �ξ�¤����ꤷ����硢�¿��ͤ��Ǥ�ᤤ��ư���������˴ݤ����ȡ����и�����ɬ�� �� �ˤ�äƶ��������ꤵ��뤳�Ȥˤʤ�ޤ������Τ��Ȥ���ޥ����ץ������פȸ����ޤ���
�����ǡ����и����� 0.00159/3.14159 = 0.0005 �Ȥʤ�ޤ������Τ褦�ʾ����������뤿��ˡ����и������̾�����˦Ť�褸�����Ȥ���ɽ�路�ޤ�
(���ξ�硢�� = (��/2)��-p= 5(10)-3 = 0.005 �Ȥʤ�ޤ�) ���������äơ����и�����
(0.00159/3.14159)/0.005) ��= 0.1�� ��ɽ������ޤ���ulp �����и����ΰ㤤���������뤿��ˡ����� x = 12.35 ����˼��ޤ��������ͤ�
= 1.24 × 101 �ˤ�����ͤȤ���ɽ�魯���Ȥ��Ǥ��ޤ��������� 0.5 ulp �ǡ����и����� 0.8�ŤǤ������� 8
������ޤ������Τ��ͤ� 8 x = 98.8 �ǡ����ͤ�
8= 9.92 × 101 �Ǥ��������� 4.0 ulp �Ǥ��������и����ϰ����Ȥ��� 0.8�ŤǤ������ʤ�����и������Ѥ��ʤ�������ulp ������¬���ͤ� 8 ���礭���ʤäƤ��ޤ������̤ˡ������ ��
�ξ�硢ulp �ˤ�����и����Ϻ��� �� �η���ʬ������ư�����ǽ��������ޤ����դˡ��弰 (2) �˼����Ȥ��ꡢ0.5 ulp �Ȥ�����������ˤ��� ʬ������ư�������и����������뤳�Ȥˤʤ�ޤ����ݤ������ɽ�魯�Ǥ⼫������ˡ�� ulp ����Ѥ�������Ǥ����㤨�С��Ǥ�ᤤ��ư���������˴ݤ��Ȥ������ϡ������� 0.5 ulp �ʲ��ˤʤ�Ȥ������ȤǤ������������Ƽ�θ����������ǵ�����ݤ������ʬ�Ϥ�����ϡ����и������������ΤǤ�������ˤĤ��Ƥ� 226�ڡ����Ǿܤ���ʬ�Ϥ��ޤ����Ťϡ��Ǥ�ᤤ��ư�������ͤ�ꡢ��֥뷸���� ʬ����¿���ʤ��ǽ��������Τǡ������ˤ������η��ϡ��� �ξ������ޥ���ǤϤ��������̩�ˤʤ�ޤ���
�ݤ�������礭������������ξ�硢ulp�Ȧ� �κ���¿���Ƥ�� ������ޤ�����Τǡ����촹���ƻ��Ѥ��Ƥ⤫�ޤ��ޤ����㤨�С���ư���������� n ulp ���������������硢������ο��� log�� n �Ȥʤ�Ȥ�����̣�Ǥ�����������и����� n�� �ξ��ϡ����Τ褦��ɽ�蘆��ޤ���
contaminated digitslog�� n (3)
�ݸ��
2 �Ĥ���ư���������κ�������� 1 �Ĥ���ˡ�Ȥ��ơ������Τ�Τ��ͤ����Τ˵��ơ������Ǥ�ᤤ�ͤ˴ݤ�뤳�Ȥ��Ǥ��ޤ���������ˡ�ϡ����ڥ��ɤΥ��������礭���ʤ�ȡ�����ʬ�������Ȥ�������褦�ˤʤ�ޤ���p = 3 �Ȥ���� 2.15 × 1012 - 1.25 × 10-5 �ϼ��Τ褦�˷��Ǥ��ޤ���
x = 2.15 × 1012
y = 0.0000000000000000125 × 1012
x - y = 2.1499999999999999875 × 1012����ˤ�� 2.15 × 1012 �˴ݤ���ޤ�����ư�������б��Υϡ��ɥ��������̾�����η�٤���ͭ����ΤǤϤʤ������ꤵ�줿������оݤȤ��Ʊ黻��Ԥ��ޤ������ݤ��줿����� p �ξ�硢�����꾮�������ڥ��ɤ����˥��եȤ����ȡ��Ʒ��ñ���˴�����ޤ� (�ݤ���ޤ���)��2.15 × 1012 - 1.25 × 10-5 �ϼ��Τ褦�ˤʤ�ޤ���
x = 2.15 × 1012
y = 0.00 × 1012
x - y = 2.15 × 1012��ϡ��������Τ˷��������Ȥޤä���Ʊ���ˤʤꡢ���η�̤��ݤ���ޤ����̤����ͤ��Ƥߤޤ���10.1 - 9.93 �ϼ��Τ褦�ˤʤ�ޤ���
x = 1.01 × 101
y = 0.99 × 101
x - y = 0.02 × 101���Τʲ�� 0.17 �ʤΤǡ�����κ��� 30 ulp �Ȥʤꡢ�����η�˸����������Ƥ��ޤ����ʤ�������ۤ��礭�ʸ������Ф�ΤǤ��礦��
���� 1
- �ѥ��� b �� p ����Ѥ�����ư�������ե����ޥåȤ� p ��κ����������硢��̤����и����Ϻ��硢b - 1 �ˤʤ롣
����
- �� x - y �� �� - 1 �����и����ϡ�x = 1.00...0 ��y = .�Ѧ�...�� (�� = �� - 1) �ξ��������ޤ��������� y �η���� p �Ǥ� (���٤� ��)�����Τʺ��� x - y = ��-p �Ǥ��������� p ������Dz��������ȡ�y �κDz��̷夬���եȥ��դ���Τǡ�����κ��� ��-p+1 �Ǥ����������äơ������� ��-p - ��-p+1 = ��-p (�� - 1) �ǡ����и����� ��-p(�� - 1)/��-p = �� - 1 �Ǥ�����
�� = 2 �ξ�硢���и����Ϸ�̤�Ʊ�����餤�礭���ʤ뤳�Ȥ�����ޤ����ޤ��� = 10 �ξ�硢9 �ܤˤʤ뤳�Ȥ�����ޤ�������������ȡ��� = 2 �ξ�硢�嵭�μ� (3) �ϱ�����ο��� log2(1/��) = log2(2p) = p �ˤʤ뤳�Ȥ��ޤ������ʤ����̤� p ��Ϥ��٤Ƹ��äƤ��뤳�Ȥˤʤ�ޤ������ξ������褹�뤿��ˡ��ݸ���Ȥ��� 1 ��ʬ���ɲä��Ƥߤޤ������ʤ�������������� p + 1 ����ڤ�ΤƤơ������η�̤� p ��˴ݤ�ޤ��������ݸ�����Ѥ���ȡ�������ϼ��Τ褦�ˤʤ�ޤ���
x = 1.010 × 101
y = 0.993 × 101
x - y = 0.017 × 101�ޤ�����������ʤ�ޤ���110 - 8.59 �ξ�硢1 ����ݸ����ߤ���ȡ���̤����и����ϡ��Ť���礭���ʤ뤳�Ȥ�����ޤ���
x = 1.10 × 102
y = 0.085 × 102
x - y = 1.015 × 102�����ݤ��� 102 �ˤʤ�ޤ������������������ 101.41 �ǡ����и����� 0.006 �Ȥʤꡢ�� = 0.005 ����礭���ʤ�ޤ������̤ˤϡ���̤����и����� �Ť��鷺�����礭���ʤ�ޤ������Τ�ɽ�魯�ȼ��Τ褦�ˤʤ�ޤ���
���� 2
- x �� y �� �� �� p �Υѥ�������Ѥ����ե����ޥåȤˤʤäƤ�����ˡ� p + 1 �� (1 �ݸ��) �Ǹ�����Ԥ��ȡ���̤����и����� 2�� ��꾯�ʤ��ʤ롣
���������ˤĤ��Ƥ� �ִݤ�������Ǿ������ޤ����ʤ���x �� y ������Τ�����Ǥ��äƤ⤫�ޤ�ʤ��Τǡ��嵭�������Ǥϲû�����Ѥ��Ƥ��ޤ���
�껦
���κǸ�ι�η����ϡ��ݸ�夬�ʤ���С�2 �Ĥζᤤ�ͤǸ������������������и����ϡ��������礭���ʤ��ǽ�������롢�Ȥ������ȤǤ������ʤ������ (��������Ѥ����û� ) ��ȼ������ɾ��������̡����и������礭���ʤꤹ���ơ��夬���٤�̵��̣�ˤʤ��ǽ��������ޤ� (����1)���ߤ��˶ᤤ�ͤ�����ȡ����ڥ��ɤκǾ�̷夬���줾����פ��ơ���ߤ��껦����ޤ��������껦�ˤϰ����������� 2 ���ब����ޤ���
�������껦�ϡ����ڥ��ɤ��ݤ�����αƶ����������������ޤ����㤨�С����������κ��θ�������ˤ��� b2 - 4ac �ξ��Ǥ���b2 �� 4ac ����ư�������ξ軻�η�̤Ȥʤ�Τǡ��������ݤ�����αƶ�������ޤ������ˤ������ͤ����Ǥ�ᤤ��ư���������˴ݤ��졢���٤� 0.5 ulp ����ˤʤäƤ���Ȥ��ޤ���������Ԥ��Ȥ����껦�ˤ�ä����Τʷ夬¿���ü������ݤ�����ˤ�äƱ������줿��������Ĥ���뤳�Ȥ�����ޤ����������äơ�������� ulp ���礭���������ޤޤ���ǽ��������ޤ����㤨�С�b = 3.34��a = 1.22��c = 2.28 �Ǥ���Ȳ��ꤷ�ޤ��� b2 - 4ac �����Τ��ͤϡ�0.0292 �Ǥ����������� b2 �� 11.2 �ˡ��ޤ� 4ac �� 11.1 �ˤ��줾��ݤ����Τǡ��ǽ�Ū�ʲ�� 0.1 �Ȥʤꡢ���� 11.2 - 11.1 �� 0·1 �Ǥ��ä��Ȥ��Ƥ⡢70 ulp��θ������Фޤ� 6���������Τ������θ����ˤʤä��ΤϤʤ��������ξ軻��Ƴ�����줿���������餫�ˤʤä��Ȥ������ȤǤ���
�������������껦�ϡ����Το��̤�����Ȥ��˵����ޤ���x �� y �˴ݤ�������ʤ���硢�ݸ�����Ѥ��Ƹ�����Ԥ��ȡ����� 2 �ˤ�� x - y �κ������и��������˾����� (2�� �ʲ�) �ʤ�ޤ���
�������껦�θ����Ȥʤ�������������ѹ����뤳�Ȥˤ�ꡢ�������Ǥ����礬����ޤ����������������κ��θ�������Ƥߤޤ���
(4)
b2 ��
�ξ�硢
�ˤ��껦���Ԥ��ʤ��Τǡ�
�Ȥʤ�ޤ�����������2 �Ĥθ����Τ����Τ⤦�����βû� (����) �������Ȥʤäư������껦���Ԥ��ޤ��������������ˤϡ����Τ褦�� r1 ��ʬ�Ҥ�ʬ���軻���� (r2 �ξ���Ʊ�ͤ�)��
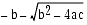
(5)
�ǡ�b > 0 �ξ�硢���� (4) ����Ѥ��� r1 �������ȡ��껦���Ԥ��ޤ����������äơ�r1 �η��ˤϸ��� (5)���ޤ� r2 �η��ˤϸ��� (4) ����Ѥ���褦�ˤ��Ƥ���������������b < 0 �ξ��ϡ�r1 �η��˸��� (4)���ޤ� r2 �η��˸��� (5) ����Ѥ��Ƥ���������
x2 - y2 �μ��Ⱝ�����껦��ȼ�������Ǥ���(x - y)(x + y) �Ȥ���ɾ�������������ΤǤ�7�����������κ��θ����Ȥϰۤʤꡢ���μ������ˤ⸺����ȼ���ޤ������ݤ��������ߤ��ʤ��������껦�ʤΤǰ����ǤϤ���ޤ������� 2 �ˤ�ꡢx - y �����и�����¿���Ƥ� 2�� ���ޤ����ޤ�������ϡ�x + y �ˤ⤢�ƤϤޤ�ޤ������и����ξ��ʤ����̤�軻���Ƥ⡢�Ѥ����и����Ͼ������ʤ�ޤ� (�ִݤ��������) ��
���Τ��ͤȷ��ͤκ�����뤿��ˡ����Τ褦��ɽ������Ѥ��ޤ����ޤ� x - y �ϡ�x �� y �����Τʺ���ɽ�魯��ΤȤ��ޤ����ޤ� x ���� y ���������ͤ�ɽ�魯���ϡ�x
y ��ɽ�����ޤ���Ʊ�ͤˡ�
��
��
�Ͻ�˲û����軻�������γƷ��ͤ�ɽ�路�ޤ������٤���ʸ���ξ�硢����δؿ��η��� (�㤨��
LN(x)��SQRT(x) �ʤ�) ��ɽ�路�ޤ�����ʸ���Ȱ���Ū�ʿ��ص���ϡ��ͤ��Τ�� (�㤨�� ln(x)���ʤ�) ��ɽ�魯��ΤȤ��ޤ���
x2 - y2 �ζ���ͤ�ɽ�魯��硢(x
y)
(x
y) �Ȥ���ɽ���Ϥ����Ƹ���Ū�Ǥ�����x �� y ����ư�����������Τ�
��
�ο����ͤζ���ͤˤʤ뤳�Ȥ�����ޤ����㤨�С�
��
����2 ��ɽ���Ǥ����Τˤ�ɽ�碌�ʤ� 10 �ʿ��Ǥ����礬����ޤ������ξ�硢x
y �� x - y �ζ���ͤ�ɽ�魯�ˤ��Ƥ⡢���μ�
-
����١����и������礭���ʤ�Τǡ�x2 - y2 ���Ф��� (x + y)(x - y) �������ϡ�����ۤ��礭���Ϥʤ��ʤ�ޤ���(x + y)(x - y) �� x2 - y2 �η���٤ϤۤȤ��Ʊ���ʤΤǡ����ξ��˸¤� (x + y)(x - y) ������ͭ���Ȥ������Ȥˤʤ�ޤ������������̤ˤϡ����Ϥ�����ͤǤϤʤ����Ȥ�¿���Τǡ��������껦���������껦���֤��������̣�Ϥ���ޤ��Ȥϸ������ǡ������������ʤ����Ǥ⡢�껦������Ū���ӽ� (���������κ��θ����Τ褦��) �Ǥ���С���̣������ޤ���������Ͽ�Ǥϡ����륢�르�ꥺ����Ф�����ư�����������Ϥ�����������̤��ǽ�ʸ¤����Τ˷�����뤳�Ȥ�����Ȥ��ޤ���
x2 - y2 �μ��ϡ�(x - y)(x + y) �Ȥ��ƽ�����ȡ��������껦���������껦���֤���������Τǡ�������Τˤʤ�ޤ���
���ˡ��������껦���������껦���֤������뤳�ȤΤǤ�����������Ҳ𤷤ޤ���
���ѷ������Ѥϡ����Τ褦�� 3 �� a��b��c ��Ĺ����ľ��ɽ�魯���Ȥ��Ǥ��ޤ���
���ѷ�������ʿ���������Ǥ��� (a
b + c) �Ȳ��ꤷ�ޤ���s
a �Ȥʤ�Τǡ��� (6) �ι� (s - a) �Ǥϡ�2 �Ĥζᤤ�� (�����˴ݤ�������ޤޤ���ǽ��������ޤ�) �θ�����Ԥ��ޤ����㤨�� a = 9.0��b = c = 4.53 �ξ�硢�������ͤ� 9.03 �� A �� 2.342...�Ȥʤ�ޤ������� s (9.05) �� 2 ulp �θ���������ޤ�����A �η��ͤ� 3.04 �ʤΤǸ����� 70 ulp �Ȥʤ�ޤ���
ʿó�ʻ��ѷ��ξ��Ǥ⡢���Τʷ�̤�������褦�ˡ����� (6) �Τ褦�˽����뤳�Ȥ��Ǥ��ޤ� (Kahan��1986)��
a��b��c �� a �� b �� c �ξ����������ʤ����ϡ����줾���̾�����ѹ����Ƥ��顢���� (7) ����Ѥ��ޤ��� (6) �� (7) �α��դ����Ū��Ʊ��Ǥ��뤳�Ȥ����Ū��ñ�˥����å��Ǥ��ޤ���a��b��c ���ͤˤ�ꡢ���� 2.35 �������ޤ������θ����� 1
ulp�ǡ��ǽ�θ������Ϥ뤫�����ΤǤ��뤳�Ȥ��狼��ޤ���������ξ�硢���� (7) �ϸ��� (6) ���Ϥ뤫�����ΤǤ���Τǡ����̤˸��� (7) ��ͭ���Ǥ���ȸ����ޤ���
���� 3
- ���� (7) ����Ѥ��ƻ��ѷ������Ѥ���Ȥ��˵�����ݤ�����ϡ��ݸ��Ǹ�����Ԥ��� e �� 0.005 �ǡ�ʿ������ 1/2 ulp �ʲ����ϰϤǷ������¤ꡢ11��������ޤ����롣
e < 0.005�Ȥ������ϡ����¾夢������ư�����������ƥ����������ޤ����㤨�С��� = 2 �ξ�硢 p �� 8 �Ǥ���С�ɬ�� e < 0.005 �ˤʤꡢ�� = 10 �Ǥ���� p �� 3 �ǽ�ʬ�Ȥ������Ȥˤʤ�ޤ���
�������и����˴ؤ������� 3 �ε��ҤǤϡ�������ư�������黻�ˤ�äƷ�����뤳�Ȥ��狼��ޤ����ºݤˡ����и����ϼ��˴ؤ����ΤǤ���
SQRT((a(b
c))
(c
(a
b))
(c
(a
b))
(a
(b
c)))
4 (8)
���� (8) �ι�¤��ʣ���������Ȥ�Ǥ���Τǡ������ε��ҤǤϡ�E ����դ���ɽ����ɽ�魯�ΤǤϤʤ���E �η����Ȥ��ư����ޤ���
�������ϰϤ����Ū�������礬����ޤ����嵭�Τ褦�ʿ��ͤ���ξ�硢���� (7) �η��ͤ� 2.35 �ǡ��������ͤǤ��� 2.34216 ����Ӥ���ȡ����и����� 0.7�ŤȤʤ�ޤ�������ϡ�11�Ť��Ϥ뤫�˾������ͤǤ����������ϰϤ����������Ū�ϡ����Τʶ��������ꤹ�뤳�ȤǤϤʤ��������˿��ͤ����꤬¸�ߤ��ʤ����Ȥ��ǧ���뤳�Ȥˤ���ޤ���
�������껦���ѹ��Ǥ���Ǹ����� (1 + x)n (������
) �Ǥ������μ��϶�ͻ���Ǥ褯���Ѥ���ޤ����㤨�С�ǯΨ 6 % �ζ�Ը��¤����� 100 �ɥ뤺���¶⤷������ʣ���������ͤ��Ƥߤޤ���n = 365 �ǡ�i = 0.06 �Ȥ���ȡ�1 ǯ������߳ۤ�
�� = 2�� p = 24 �Ȥ��Ʒ�����ȷ�̤� $37615.45 �Ȥʤꡢ�ºݤζ�ۤ� $37614.05 �Ȥ� $1.40 �κ����Фޤ��������������ͳ�ϴ�ñ�Ǥ����� 1 + i/n �Ǥϡ�0.0001643836 �� 1 ��û�����Τǡ�i/n �β��̥ӥåȤ�������Ȥ������ȤǤ������δݤ�����ϡ�
1 + i/n �� n �褹��ȡ��������ޤ���(1 + i/n)n �Ȥ���ʣ���ʼ��� enln(1 + i/n) �Ƚ����뤳�Ȥ��Ǥ��ޤ������ξ�������ϡ�x ������������ ln (1 + x) �η��Ǥ���1 �Ĥ���ˡ�Ȥ��� ln (1 + x)
x �ζ���ͤ���Ѥ��뤳�Ȥ��Ǥ��ޤ������ξ�硢��ʧ���� $37617.26 �Ȥʤꡢ������ $3.21 �ʤΤǡ�ñ��ʸ����������٤�����ޤ��������������� 4 �˼����Ȥ��ꡢ(1 + x) ������Τ˷�������ˡ������ޤ� (HP��1982ǯ)�����θ����ˤ�ꡢ$37614.07 �Ȥ�����̤�����졢�������鷺�� 2 ����Ȱ���ˤʤ�ޤ���
���� 4 �Ǥϡ�
LN(x)�ˤ�� ln (x) �ζ���ͤ� 1/2 ulp ����θ����ǵ����뤳�Ȥ�����Ȥ��ޤ�������ˤ�ꡢx ���ͤ��������Ȥ��ˡ�1x ����x �β��̥ӥåȤˤ��������Ӽ����뤿��ˡ�
LN(1x) �ˤ�� ln (1 + x) �ζ���ͤ������ʤ����꤬��褵��ޤ������ʤ����
�ΤȤ��ˡ�ln (1 + x) �η��ͤϼºݤ��ͤζ���ͤˤϤʤ�ʤ��Ȥ�������Ǥ���
���� 4
- ln (1+ x) �θ����Ƿ�������硢
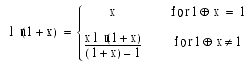
- �ݸ�����Ѥ��Ƹ�����Ԥ���e < 0.1���ޤ��� ln �� 1/2 ulp ����θ����Ƿ�����ȡ�0 �� x <
�ξ������и����� 5e ����Ȥʤ롣
���θ����ϡ�x ���ɤΤ褦���ͤǤ��äƤ�Ŭ�Ѥ���ޤ�����
�ξ�硢���ʤ������θ��� ln (1 + x) �ǰ������껦������������˸¤��̣������ޤ��������ϰ츫����̣�����Τ褦�˻פ��ޤ��������줬������ư�����ͳ�ϴ�ñ�Ǥ���ln (1 + x) ��
�Ƚ����Ƥߤޤ������դ����ǤϤ��Τޤ��Ǥ��ޤ�
�������դ����� ��(x) = ln(1 + x)/x �ϡ�x �� 1 ��û�����Ȥ����礭�ʴݤ�����������ޤ�����������ln(1 + x)
x �Τ��� �� �ϤۤȤ������Ǥ����������äơ�x ��鷺�����ѹ���������Ǥ⡢�礭�ʸ�����ȼ���ޤ���
���ʤ����
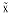
�ξ�硢
(
) �������ȡ�x��(x) = ln(1 + x) �Τۤܶ���ͤ������ޤ���
��
+ 1 �����������Ǥ���
���ͤ�����Ǥ��礦����1 +
�Ϥ��礦�� 1
x �ˤʤ�Τǡ�
= (1
x)
1�Ȥ����ͤǤ���
���ι�η����Ȥ��ơ����Τζᤤ�ͤ�����Ȥ� (�������껦��ȼ��) �ϡ��ݸ��ˤ�����٤��ݾڤ����Ȥ������Ȥ������ޤ��������Τʷ�̤�⤿�餹�����ϡ��������껦����Ѥ��ơ����ͤ����٤�夲�뤳�Ȥˤ�ꡢ�����뤳�Ȥ��Ǥ��ޤ�����������������ˡ���ݸ�����Ѥ��Ƹ�����Ԥ����˸¤����ѤǤ��ޤ����ޤ��ݸ�����Ѥ��Ƥ⡢�û���ΥӥåȤ� 1 ��¿���ʤ�����ʤΤǡ�����ۤɤε�����ȼ���ޤ����㤨�� 54 �ӥåȤ������ٲû���ξ�硢;ʬ�ʥ����Ȥ� 2 % ���٤ǺѤߤޤ����������٤Υ����Ȥˤ�äơ����ѷ������Ѥ������� (6) �估 ln (1 + x) �ʤɤ�¿���Υ��르�ꥺ���¹Ԥ��������������ޤ����Ƕ�Υ���ԥ塼���ˤ��̾�ݸ�夬�Ѱդ���Ƥ���Τǡ�������б��Ǥ��ʤ������ƥ�ϡ��ۤȤ�ɤ���ޤ��� (Cray �����ƥ�ʤɤ�����ޤ�)��
���Τʴݤ����
�ݸ�����Ѥ�����ư�������黻��Ԥ��ȡ����Τ˷�������ǺǤ�ᤤ��ư���������˴ݤ�����⡢���٤�����ޤ�����Ԥη���ˡ������Τʴݤ�����פȸ����ޤ� 8������ 2 �����˾Ҳ𤷤���ϡ�1 ��ʬ���ݸ�����ݤ�������Ȥ��äơ�ɬ���������Τʷ�̤�������Ȥϸ¤�ʤ����Ȥ��Ƥ��ޤ������ι�ˤϡ�������ư����ݾڤ��뤿��ˡ��ݸ�����Ѥ��륢�르�ꥺ�������Ĥ��Ҳ𤷤ޤ����������Ǥϡ����Τʴݤ��Ԥ�����Υ��르�ꥺ�������ޤ���
�����ޤǤ��ʳ��Ǥϡ��ޤ��ݤ��������Ƥ��ޤ��ݤ�����ϡ��ڤ겼�����ڤ�夲�ζ��ڤ��ɤ����դ��뤫�Ȥ����� (�㤨�С�12.5 �� 12 �Ȥ��뤫 13 �Ȥ��뤫�Ȥ�������) �������������ޤ���1 �Ĥ���ˡ�Ȥ��ơ�10 �ޤǤ��ͤ�ͼθ������ơ�0��1��2��3��4 ���ڤ�Τơ�5��6��7��8��9 ���ڤ�夲��Ȥ����ͤ���������ޤ����������äơ�12.5�� 13 �Ȥ��ư����ޤ���DEC �� VAX �ǤϤ��Τ褦�ʻͼθ��������Ѥ���Ƥ��ޤ����ޤ���5 �ǽ������� 2 �Ĥδݤ���ˡ�Τ��礦�ɶ��ܤˤ���Ȥ�����̣�ǡ��ݤ��Ԥ�������Τ�Ⱦʬ���ڤ�夲��Ⱦʬ���ڤ겼����Ȥ����ͤ����⤢��ޤ������� 50% ���� 2 ʬ����Ȥ�����ˡ�ˤϡ��ݤ�η�̤����ʤ��Ƥ⡢�Dz��̤η夬�����ˤʤäƤ��ʤ���Фʤ�ʤ��Ȥ�������ȼ���ޤ����������äơ�12.5 �ϡ�2 �������Ǥ��뤿�ᡢ13 �ǤϤʤ���12 ���ڤ�ΤƤ��ޤ����ڤ�夲�ȶ����ؤ��ڤ�ΤƤΤɤ��餬�褤���Ȥ�������ˤĤ��ơ�Reiser �� Knuth �϶����ؤ��ڤ�ΤƤ�����˾�ޤ����Ȼ�Ŧ���Ƥ��ޤ� (1975)��
���� 5
- x �� y ����ư���������Ȥ��ơ�x0 = x�� x1 = (x0
y)
y��...��xn =(xn-1
y)
y ��������롣
��
������ؤ��ڤ�ΤƤˤ��Ʊ���褦�˴ݤ��ȡ����٤Ƥ� n �ˤĤ��� xn = x���ޤ� n �� 1 �Τ��٤ƤˤĤ��� xn = x1 �Ȥʤ롣��
���η�̤�ʬ�ह���ǡ�x = 1.00��y = -0.555 �Ȥ��� �� = 10�� p =3 �ξ���ͤ��Ƥߤޤ���������ڤ�夲���硢x0
y = 1.56��x1 = 1.56
0.555 = 1.01��
x1y = 1.01
0.555 = 1.57�Ȥ����������ˤʤꡢxn = 9.45 (n �� 845) �ˤʤ�9 �ޤǡ�xn ��Ϣ³�ͤ� 0.01 ���Ȥ������Ƥ����ޤ����������ڤ�ΤƤ��硢xn �ϤĤͤ� 1.00 �ˤʤ�ޤ���������ϡ��ڤ�夲�Υ롼�����Ѥ���ȡ�����̤��������˾����ˤ���Ƥ����������������ؤ��ڤ�ΤƤ���Ѥ���ȡ����Τ��줬�����ʤ����Ȥ��Ƥ��ޤ������θ�������Ǥϡ������ؤ��ڤ�ΤƤ��Ӥ��ƻ��Ѥ��뤳�Ȥˤ��ޤ���
¿�����٤α黻�Ǥϡ����Τʴݤ 1 ������Ԥ��ޤ������٤�夲��ˤϡ�2 �Ĥδ���Ū�ʥ��ץ�����������ޤ���1 �Ĥϡ��������礭��ͭ�շ����Ѥ�����ư���������Ǥ�������ͭ�շ�ϥ������˳�Ǽ���졢������֥����Ǥ����ο������뤿��Υ롼����Υ����ǥ����Ԥ��ޤ����⤦ 1 �ĤΥ��ץ������ϡ��̾����ư��������������Ȥ��Ƥ���˹⤤���٤���ư����������ɽ�魯��ˡ�Ǥ������ξ�硢̵�¤����٤��������Ǥ��ɲä��뤳�Ȥˤ�ꡢ�⤤���٤���ư�����������������ޤ��������Ǥϡ�2 ���ܤΥ��ץ������ˤĤ����������ޤ�����ư�����������������Ѥ��������ϡ��������ˤ��ܿ���ǽ�ʷ��ǥ����ǥ��Ǥ��뤳�Ȥˤ���ޤ�������ȿ�̡����Τʴݤ�α黻��ɬ�פˤʤ�ޤ���
���Υ����ƥ�ˤ�����軻�ν��פ����ϡ��Ʋÿ��� x y ��Ʊ�����٤���Ĥ褦�ˡ�x y ���Ѥ��¤Ȥ���ɽ�魯���Ȥˤ���ޤ�������ϡ�x �� y ��ʬ�䤹�뤳�Ȥˤ�äƹԤ��ޤ���x = xh + xl ��y = yh + yl �Ƚȡ��ºݤ��Ѥ� xy = xhyh + xh yl + xl yh + xl yl �Ȥʤ�ޤ��� x �� y �� p �ӥåȤ�ͭ�շ夬������ [p/2] �ӥåȤ� xl��xh��yh��yl ��ɽ�魯���Ȥ��Ǥ���С��ÿ���ͭ�շ�� p �ӥåȤˤʤ�ޤ��� p �������Ǥ���С���ñ��ʬ��Ǥ��ޤ���x0.xl...xp -1�ο��ϡ�x0.xl...xp/2 - 1 �� 0.0 ... 0xp/2 ... xp - 1 ���¤Ȥ���ɽ�魯���Ȥ��Ǥ��ޤ���������p ������ξ�硢���Τ褦�˴�ñ�ˤ�ʬ��Ǥ��ޤ����������������Ѥ��ơ�1 �ӥå�ʬ���ɲäǤ��ޤ����㤨�С��� = 2�� p = 5��x = 0.10111 �ξ�硢x �� xh= 0.11������� xl = -0.00001�Ȥ���ʬ��Ǥ��ޤ���Dekker (1971) �ˤ��ȡ�ʬ����ˡ�ϴ�ñ�Ǥ�����1 ����ݸ��ʳ��ˤ�;ʬ�˷夬ɬ�פǤ���
���� 6
- �� > 2 �Ǥ��äƤ� p �������Ǥ���Ȥ������¤Τ�Ȥˡ�p ����ư���������٤Ȥ��ơ���ư�������������Τ˴ݤ���ΤȤ��롣���ΤȤ���k = [p/2] �����٤�Ⱦʬ (�ڤ�夲) �ǡ�m = ��k + 1 �Ȥ���ȡ�x �� x = xh + xl (������
xh = (mx)
(m
x
x)��xl = x
xh �ǡ��� xi �� [p /2] �ӥå����٤�ɽ����ǽ�Ȥ���) �Ȥ���ʬ��Ǥ��롣
�����������ºݤ���ˤɤΤ褦��Ŭ�Ѥ���뤫�뤿��ˡ��� = 10�� p = 4��b = 3.476��a = 3.463��c = 3.479 �Ǥ���Ȳ��ꤷ�ޤ���b2 - ac ��Ǥ�ᤤ��ư���������˴ݤ��ȡ�0·03480�ˤʤꡢb
b = 12.08��a
c = 12.05 �ˤʤ�ޤ����������äơ�b2 - ac �η��ͤ� 0·03�Ȥʤ�ޤ�������ˤ� 480 ulp �θ���������ޤ������� 6 �ˤ�ȤŤ��� b = 3.5 - 0.024��a = 3.5 - 0.037��c = 3.5 - 0.021 �Ȥ���ȡ�
b2 �� 3.52 - 2 × 3.5 × 0.024 + 0.0242 �Ȥʤ�ޤ����Ʋÿ��Ϥ��٤����ΤʤΤǡ�
b2 = 12.25 - 0.168 + 0.000576 �ˤʤ�ޤ� (���λ������¤�ɾ���Ϥ���Ƥ��ޤ���)��Ʊ���褦�ˡ�ac = 3.52 - (3.5 × 0.037 + 3.5 × 0.021) + 0.037 × 0.021 = 12·25 - 0.2030 + 0.000777 �ˤʤ�ޤ����Ǹ�ˡ�2 �Ĥ�Ϣ³�ऴ�Ȥ˸�������ȡ�b2 - ac �ζ���ͤ�
00.0350
0.000201= 0.03480 �Ȥ��Ƶ����ޤ�������ϡ����Τ˴ݤ���η�̤Ȱ��פ��ޤ������� 6 �����Τʴݤɬ�פˤʤ뤳�Ȥ��ǧ���뤿��ˡ�p = 3���� = 2��x = 7������� m = 5��mx = 35��m
x = 32 �����ͤ��Ƥߤޤ���1 ����ݸ�����Ѥ��Ƹ�����Ԥ��ȡ�(m
x )
x = 28 �Ȥʤ�ޤ����������äơ�xh = 4��xl = 3 �Ȥʤ�Τǡ�xl �� [p /2] = 1 �ӥåȤǤ�ɽ�碌�ޤ���
���Τʴݤ�κǸ����Ȥ��ơ�m �� 10 �ǽ����������ͤ��Ƥߤޤ������η�̡����̤ˤ� m/10 �˰��פ��ʤ���ư���������������ޤ����� = 2 �ξ�硢���Τʴݤ����Ѥ��ơ�m/10 �� 10 ��ݤ���ȡ��ԻĤʤ��Ȥ� m ���ꥹ�ȥ�����ޤ����ºݤˤϡ�����˰���Ū�ʻ��¤����ƤϤޤ�ޤ� (Kahan)�������Ͼܺ٤ˤ錄���ΤǤ��������Τ褦�ʾܤ��������ޤǴؿ��Τʤ����ϡ���IEEE ɸ����ޤ��ɤ����Ф��Ƥ⤫�ޤ��ޤ���
���� 7
- �� = 2 �ΤȤ���m �� n �� |m|<2p - 1 �������ǡ�n �� n = 2i + 2j �Ȥ����ü�ʷ����������硢��ư�������黻�����Τ˴ݤ��Ȥ���С� (m
n )
n �� m �Ȥʤ롣
����
- 2 �Τ٤���ǥ����������Τϡ�ͭ�շ�ǤϤʤ���ñ�˻ؿ����ѹ����������ʤΤǡ����ƶ��Ϥ���ޤ���q = m/n �ξ�硢2p - 1 �� n < 2p �Ȥʤ�褦�� n ���������
< q < 1 �Ȥʤ�褦�� m ��������ޤ����������ä� 2p - 2 < m < 2p �Ȥʤ�ޤ���m �ˤ� p �Ĥ�ͭ�եӥåȤ�����Τǡ�2 �ʾ������α��˺��� 1 �ӥåȤ�ɬ�פǤ���m �������ѹ����ƤⰭ�ƶ��Ϥʤ��Τǡ�q > 0�Ȥ��ޤ���
= m
n �ξ�硢�������������ˤϡ�����ɬ�פ�����ޤ���
(9)
- ����ϡ�m �� 2 �ʾ������α�¦�˺��� 1 �ӥåȤ����Ѥ���Ƥ���Τǡ�n
�ˤ�� m �˴ݤ���ޤ���
- ��֤ξ��ΰ����ˤĤ��Ƥϡ���n
- m��=
�ξ��ˡ�����������Ƥ��ʤ������ m �ϡ�m��< 2p - 1���ޤ����̥ӥåȤ� 0 �ˤʤ�Τǡ����������� m �β��̥ӥåȤ� 0 �ˤʤ�ޤ����������äơ���֤��ͤ� m �˴ݤ���ޤ���
q = .q1q2 ...��= .q1q2 ... q p 1 �Ǥ���Ȳ��ꤷ�ޤ���|n
- m|�ζ���ͤ����ˤ�
�ޤ�����- q��=��N/2p + 1 - m/n�� (N�ϴ��������) ������ޤ���n = 2i + 2j������� 2p - 1 �� n < 2p �Ǥ��뤫�顢����� k �� p - 2 �ˤĤ��Ƥ� n = 2p - 1 + 2k �Ǥʤ���Фʤ�ޤ��������äơ����Τ褦�ˤʤ�ޤ���
- ʬ�Ҥ������Ǥ���N �ϴ���ʤΤǡ��ºݤˤϴ���������Ȥʤ�ޤ����������äơ�
��- q�á� 1/ (n2 p+1-k ) �Ȥʤ�ޤ���q <
(q >
�ξ���Ʊ��) �Ȳ���10����ȡ�
n< m�ǡ����Τ褦�ˤʤ�ޤ���
- ��m-n
��= m-n
= n(q-
) = n(q-(
-2-p-1) ) ��
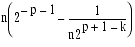
- = (2p-1+2k)2-p-1+2-p-1+k =
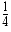
- ����ˤ�ꡢ (9) ������Ω������������������뤳�Ȥˤʤ�ޤ�11����
�����ϡ�2i + 2j ���i + ��j ���֤�������¤ꡢǤ�դδ�� �� �ˤĤ��ƿ��ˤʤ�ޤ��������� �� ���礭���ʤ�˽��äƦ�i + ��j ��ʬ��κ����礭���ʤäƤ����ޤ���
�����ǡ�����Ͽ�κǽ�������ִ���Ū�ʱ黻������¿���δݤ�������Ф뤳�Ȥ˲������꤬���뤫���פȤ�������Ū�ʵ����Ω���֤뤳�Ȥˤ��ޤ������������ϡ��礤������Ϥ���פǤ���������ͳ�ϡ����Τʴ��ܱ黻�Ǥ����и������㤯�ޤ�����Ȥ�����̣�ǡ������Ρ��������פ�����Ǥ��뤫��Ǥ���
�Ƹ����ˤ鷺�������и�����ȼ���Ȥ�����̣�ǡ����������������Ȥ�����Ǥ���Ȥ�����ͳ�ˤ�äơ��ݤ����������Ϥ���Ȥ������Ȥˤʤ�ޤ������껦���Ǥϡ��ݸ�����Ѥ��륢�르�ꥺ��ˤ�äƤϡ��嵭�ΰ�̣����������̤��������Τ�������������ޤ������������������θ����ؤ����Ϥ��������Τ�¬��ˤ�ȤŤ����ͤǤ����硢���� 3 �� 4 �Ǹ���������̵��̣�ˤʤäƤ��ޤ���������ͳ�ϡ�x �� y ��������¬���ͤζ���ͤǤ����硢�������껦 x - y ���������Ѥ�뤫��Ǥ��������������Τʷ��ϡ����� 6 �� 7 �Ǽ��������Τʴط���¾ڤǤ���Ȥ�����̣�ǡ��ǡ����������Τʾ��Ǥ�ͭ���Ǥ��뤳�Ȥ˰㤤�Ϥ���ޤ�����ư�������ѿ������줾�졢�ºݤ��ͤζ���ͤˤ����ʤ����Ǥ�ͭ���Ǥ���Ȥ������ȤǤ���
IEEE ɸ��
��ư�������黻�ˤϡ�IEEE 754 �� IEEE 854 �Ȥ��� 2 �Ĥ�ɸ�ब����ޤ���IEEE 754 �ϡ�ñ���٤ξ�� �� = 2�� p = 24���ޤ������٤ξ�� p = 53 ����Ѥ��� 2 �ʿ�ɸ��Ǥ� (IEEE 1987)������ɸ��ˤ�ꡢñ���٤������٤ξ������Τʥӥåȡ��쥤�����Ȥ����ꤵ��ޤ���IEEE 854 �Ǥϡ��� = 2���ޤ��� �� = 10 �Τ����줫����Ѥ��ޤ���IEEE 754 �ȰۤʤꡢIEEE 854 �ξ�����ư����������ӥåȤ���沽��������ϻ��ꤵ��ޤ��� (Cody�ۤ� 1984)��p ���Ф���������ͤ�ɬ�פ���ޤ���ñ���٤������٤�ǧ����� p ���ͤ����¤���ޤ����ʤ� IEEE ɸ���Ȥ����Ѹ�ϡ��ʾ� 2 �Ĥ�ɸ��˶��̤���������ɽ�魯���˻��Ѥ��ޤ���
�ܹ�Ǥϡ�IEEE ɸ��γ��פˤĤ����������ޤ����ʹߤγƹ�Ǥϡ�����ɸ��γ������ȡ����줬���Ѥ��줿��ͳ���ޤ����ʤ� IEEE ɸ�ब�Ǥ�ͥ�줿��ư������ɸ��Ǥ��뤫�ɤ�����ʬ�Ϥ���Τ��ܻ����μ�ݤǤϤʤ��Τǡ������ޤ�ɸ��Ȥ��Ƥ��Τޤ������졢���δ��ܳ�ǰ���������뤳�Ȥˤ��ޤ����ܺ٤ˤĤ��Ƥϡ�IEEE ɸ�༫�Τλ����Ȥ��Ƥ������� (IEEE 1987��Cody �ۤ���1984)��
�ե����ޥåȤ����
���
IEEE 854 �� �� = 10 �����Ѥ���Ƥ�����ͳ�����餫�Ǥ������ 10 �ϡ�����Ū�˿Ƥ��ߤ䤹�����Ǥ��뤫��Ǥ����� = 10 �ϡ��ä˷���̤� 10 �ʿ���ɽ�魯�褦������ʤɤ�Ŭ���Ƥ��ޤ���
IEEE 854 �ǡ������ 10 �ʳ��ξ���ɬ�� 2 ����Ѥ�����ͳ�Ϥ����Ĥ�����ޤ��������и����� ulp���ǡ���ͳ�� 1 �Ĥ��������ޤ������� �� 2 �ˤ���ȡ����и����Ȥ��Ʒ�������硢0.5 ulp �δݤ������ �� ���ܿ�����ư����Τǡ�������ʬ�Ϸ�̤��Ϥ뤫�˸������ʤꡢ���и����ˤ�ȤŤ������ϤۤȤ�ɤξ�硢ñ���ʬ�ϤǤ���Ȥ�����ͳ�Ǥ����ޤ���������礭����������ͭ�������٤˴ؤ�����ͳ��ͤ����ޤ����� = 16�� p = 1 �ȡ��� = 2�� p = 4 �ξ�����Ӥ��Ƥߤޤ���������Υ����ƥ��ͭ�շ�� 4 �ӥåȤȤ��ޤ����㤨�С�15/8 ������ޤ����� = 2 �ξ�硢15 �� 1.111 × 23 �ȡ��ޤ� 15/8 �� 1.111 × 20 ��ɽ������ޤ����������äơ�15/8 �Ϥ��Τޤ����Τ�ɽ�蘆��ޤ����������� = 16 �ξ�硢15 �� F × 160 (F �� 15 ���б����� 16 ��ɽ��) ��ɽ�路�ޤ�����������15/8 �� 1 × 160�Ȥʤꡢ�������ӥåȤ� 1 �ӥåȤ�������ޤ����̤ˡ���� 16 ����Ѥ���Ⱥ��� 3 �ӥåȤ����Ȥ�����Τǡ� p �� 16 �ʷ�����٤ϡ�ͭ�����٤� 2 �ʤ� 4p ʬ�ǤϤʤ���4p -3 �ˤޤ��㲼���뤳�Ȥ�����ޤ����� ���ͤ��礭���ʤ�˽��äơ������������꤬�ФƤ���Ȥ���С�IBM �� System/370 �ˡ��ʤ� �� = 16 ����Ѥ����ΤǤ��礦�����ο��դ� IBM �ʳ����Τ�褷�⤢��ޤ���2 �Ĥ���ͳ���ͤ����ޤ����ޤ����ؿ����ϰϤ�������Ȥ������Ǥ���System/370 ��ñ���٤Ǥϡ��� = 16 �� p = 6 �����Ѥ���Ƥ��ޤ����������äơ�ͭ�շ�ˤ� 24 �ӥåȤ�ɬ�פˤʤ�ޤ���24 �ӥåȤ� 32 �ӥåȤ˼��ޤ�Τǡ��ؿ��Ѥ� 7 �ӥåȤ�����Ѥ� 1 �ӥåȤ��Ĥ�ޤ����������äơ�ɽ����ǽ�ʿ������ϰϤ� 16-2 6���� 162 6 = 22 8 �ˤʤ�ޤ����� = 2 ��Ʊ���ؿ��ϰϤ���ݤ���ˤϡ��ؿ�ʬ�� 9 �ӥåȤ�ɬ�פȤʤꡢͭ�շ�ˤϤ鷺�� 22 �ӥåȤ������ѤǤ��ޤ��������� = 16 �Ȥ���ȡ����ҤΤȤ��ꡢͭ�����٤� 4p - 3 = 21�ӥåȤˤޤ��㲼����Ȥ������꤬����ޤ�������⡢�� = 2 �� 1 �ӥå�ʬ�����٤�夲�� (�ܹ�Ǹ��) ���Ȥ��Ǥ�����ϡ�����˰����ʤ�ޤ����������äơ��� = 2 �Υޥ���ˤϡ��� = 16 �Υޥ���� 21 �� 24 �ӥåȤ��������� 23 �ӥå�ʬ�����٤����ݤ���ޤ���
IBM �� �� = 16 ����Ѥ����⤦ 1 �Ĥ���ͳ�ϥ��եȤ˴ؤ����ΤǤ���2 �Ĥ���ư����������û��������ˡ��ƻؿ����ۤʤäƤ���ȡ�����ΰ��֤��碌�뤿��ˡ������줫��ͭ�շ�եȤ��ʤ���Фʤ�ʤ����Ȥ�����ޤ������줬�����ǥѥե����ޥ��㲼���뤳�Ȥ�����ޤ����� = 16��p = 1 �Υ����ƥ�Ǥϡ�1��15 �ޤǤο��Ϥ��٤ƻؿ���Ʊ���ˤʤ�Τǡ�(
) = 105 �Τɤ��Ȥ߹�碌��û����Ƥ⥷�եȤ�ɬ�פ���ޤ���������= 2��p = 4 �Υ����ƥ�Ǥϡ������ο��λؿ����ϰϤ� 0��3 �ʤΤǡ�105 �ڥ��Τ����� 70 �ˤĤ��Ƥϥ��եȤ�ɬ�פˤʤ�ޤ���
�Ƕ�Υϡ��ɥ������Ǥϡ����ڥ��ɤΥ��֥��åȤ��Ф��륷�եȤ��Ƥ⡢�ѥե����ޥ塢����ۤ��礭�������������ʤ��Τǡ���֥�ξ��ʤ� ��= 2 ������ͭ���ʴ���Ǥ���ȸ����ޤ�����= 2 �Τ⤦ 1 �Ĥ������ϡ�ͭ�շ��;ʬ�ʥӥåȤ����������Ǥ�12����ư����������ɬ�������������Τǡ�ͭ�շ�κǾ�̥ӥåȤ�ɬ�� 1 �ˤʤꡢ������б�����ӥåȤ�̵�̤ˤ���Τϰ�̣������ޤ����μ�ˡ�����Ū�����Ѥ����ե����ޥåȤΤ��Ȥ������ӥå��פȸ����ޤ�������ư�������ե����ޥåȡ��Ǥϡ�0 ���Ф����ü�ʵ���ɬ�פǤ��뤳�Ȥ��������ޤ����������Ǽ�������ˡ�ϡ�emin - 1 �λؿ��ȡ����٤ƥ�����ͭ�շ�ˤ�ꡢ
�ǤϤʤ���0 ��ɽ�魯�Ȥ�����ΤǤ���
IEEE 754 ��ñ���٤ϡ�����Ѥ� 1 �ӥåȡ��ؿ��Ѥ� 8 �ӥåȡ������ͭ�շ��Ѥ� 23 �ӥåȤ���Ѥ��ơ�32 �ӥåȤ��ɤ��ޤ���������������ӥåȤ���Ѥ���Τǡ�23 �ӥåȤ�������Ѥ��ƥ����ɤ������Ǥ⡢ͭ�շ�� 24 �ӥå� (p =24) �ˤʤ�ޤ���
����
IEEE ɸ��Ǥϡ�ñ���١������١���ĥñ���١�����ӳ�ĥ�����٤Ȥ��� 4 ����Υե����ޥåȤ�������Ƥ��ޤ���IEEE754 �ξ�硢ñ���٤������٤Ϥۤܡ�����ʬ����ư�������ϡ��ɥ��������ᤵ��뵡ǽ���б����뤳�Ȥ��Ǥ��ޤ���ñ���٤Ǥ� 32 �ӥåȤΥ����ɡ��ޤ������٤Ǥ� 2 ��Ϣ³���� 32 �ӥåȥ�ɤ���ͭ����ޤ�����ĥ���٤ϡ����٤�¿���夲���ؿ����ϰϤ��ĥ�����ե����ޥåȤǤ�
(ɽ D-1) ��
ɽ D-1 IEEE 754�ե����ޥåȤΥѥ��� p 24 ��32 53 ��64 emax +127 ��1023 +1023 > 16383 emin -126 ��-1022 -1022 �� -16382 �ؿ����� (�ӥå�) 8 ��11 11 ��15 �ե����ޥåȤ��� (�ӥå�) 32 ��43 64 ��79
IEEE ɸ��ϡ���ĥ���٤ˤ�ä��ɲä���;ʬ�ʥӥåȿ��β��¤�������ꤷ�ޤ�����ĥ�����٥ե����ޥåȤκ�����Ƹ��٤ϡ����ɽ�ˤ��� 79 �ӥåȤˤʤäƤ��ޤ������ص��� 80 �ӥåȥե����ޥåȤȸƤФ�뤳�Ȥ�����ޤ���������ͳ�ϡ���ĥ���٤Υϡ��ɥ����������Ǥϰ��̤˱���ӥåȤϻ��Ѥ��ʤ��Τǡ�79 �ӥåȤǤϤʤ���80 �ӥåȤ���Ѥ��뤫��Ǥ���13
IEEE ɸ��Ǥϡ���ĥ���٤˺Ǥ�������֤����Τǡ������٤˴ؤ���侩�ϲ��⤢��ޤ�������ˡ����ݡ��Ȥ����Ǥ�����ܥե����ޥåȤ��б������ĥ�ե����ޥåȤ�ץ���Ȥ���褦�˶����侩����Ƥ��ޤ���
��ĥ���٤����Ѥ��줿��ͳ�ϡ�����ˤ��Ȥ���������ޤ���������̾10 �����Ѥ��ޤ���������Ū�ˤ� 13 �����Ѥ��ޤ���13 ��Τ�����10 �������ɽ�����뤳�Ȥˤ�ꡢ����ϰ츫���ؿ�����������ʤɤδؿ��� 10 ��ޤǤ����٤Ƿ�����֥֥�å��ܥå����פ���Ѥ��Ƥ���褦�˻פ��ޤ����ؿ����п�����������ʤɤδؿ��� 10 ��ޤǤ����٤����Ū��Ψ�褯���Ǥ�������Ǥϡ�;ʬ�ʷ夬�����Ĥ�ɬ�פˤʤ�ޤ�����ɡ�500 ��˥å����٤θ������п��ζ���ͤ������ͭ�����Ĥ���ΤϤ���ۤ����Ϥ���ޤ��������äơ�13 �����Ѥ��Ʒ����뤳�Ȥˤ�ꡢ10 �����������������褦�ˤʤ�ޤ�������;ʬ�� 3 �ӥåȤ�ӥåȤȤ��ƻ��Ѥ��뤳�Ȥˤ�ꡢ���ڥ졼����ñ��ʥ�ǥ�ˤ�ä���������뤳�Ȥ��Ǥ��ޤ���
IEEE ɸ��γ�ĥ���٤�Ʊ���褦�ʺ��Ѥ���äƤ��ޤ�������ˤ�ꡢ�ƥ饤�֥���ñ���� (�ޤ���������) �ˤ�� 0.5 ulp ���٤θ������ϰϤǸ�ΨŪ�˷��Ǥ���褦�ˤʤ�ޤ����������äơ��桼������ñ��ʥ�ǥ�ˤ�äƳƥ饤�֥�����Ѥ��뤳�Ȥ��Ǥ��ޤ����㤨�С��軻���п��θƤӽФ��ʤɤ˸¤餺������Ū�����ˤ�äƤ⡢0.5 ulp ����θ��������Τ��ͤ��֤����褦�ˤʤ�ޤ�����������ĥ���٤���Ѥ���Ȥ��ϡ��������Ѥ��Ƥ��뤳�Ȥ�桼�����ˤ����餫�ˤ��뤳�Ȥ����פǤ����㤨�С������ɽ�������ͤ�����ɽ������ɽ��������Ʊ�����٤Ǵݤ���Ƥ����硢�ʹߤ����η�̤ϱ���ӥåȤ˰�¸����Τǡ��桼�����ˤ�ͽ¬�Ǥ��ʤ��ʤ뤳�Ȥ�����ޤ���
��ĥ���٤ˤĤ��Ƥ���˾ܤ����������뤿��ˡ�IEEE 754 ��ñ����ɽ���� 10 �ʿ����Ѵ�����Ȥ�������ˤĤ��ƹͤ��Ƥߤޤ�����ǽ�Ǥ���С�10 �ʿ����ɤ��᤹�����ǡ�ñ���ٿ��������Ǥ���褦�ˡ���ʬ�ʷ������ݤ���ñ���ٿ�����Ϥ���Τ�����Ū�Ǥ���ñ���٤� 2 �ʿ�����������Τˡ�9 ��� 10 �ʿ�������н�ʬ�Ǥ��뤳�Ȥ��狼�äƤ��ޤ� (��2 �ʿ����� 10 �ʿ��ؤ��Ѵ����Ȥ��Ƥ�������)��10 �ʿ����դ� 2 ��ɽ�����᤹��硢1
ulp���٤ξ������ݤ���������äƤ���ä���ˤʤ�Τǡ���̿Ū�Ȥʤ�ޤ�����ĥ���٤���ΨŪ�ʥ��르�ꥺ����Բķ�Ȥʤ�褦�ʾ������������ޤ���ñ���٤ξ�硢10 �ʿ���ñ���٤� 2 �ʿ����Ѵ�����ˤϡ������ƴ�ñ����ˡ������ޤ����ޤ������� N �Ȥ��� 9 ��� 10 �ʿ����ɤ�ꡢ��������̵�뤷�ޤ���ɽ D-1 ���顢p �� 32 �ξ�硢109 < 232
4.3 × 109 �Ȥʤ�Τǡ�N ��ñ���ٳ�ĥ�ե����ޥåȤ����Τ�ɽ���Ǥ��뤳�Ȥ��狼��ޤ������� N ���������Τ�ɬ�פ� 10P �Τ٤������ޤ�������ϡ�10 �ʿ��λؿ��ȡ����λ����ޤǤ�̵�뤵�줿�������ΰ��֤��θ�����Ȥ߹�碌�ˤʤ�ޤ���10|P| ������ޤ���|P| �� 13 �Ǥ���С�1013 = 213 513 �ǡ�513 < 232 �Ȥʤ�Τǡ���������Τ�ɽ�����뤳�Ȥ��Ǥ��ޤ����Ǹ�ˡ�N �� 10|P| ��軻 (�ޤ��� p < 0 �ξ��Ͻ���) ���ޤ������κǸ�η����������Ԥ���С��Ǥ�ᤤ 2 �ʿ��������ޤ����Ǹ�ξ軻 (����) �����Τ˹Ԥ���ˡ�ˤĤ��Ƥϡ���2 �ʿ����� 10 �ʿ��ؤ��Ѵ����Ǿܤ����������Ƥ��ޤ����������äơ�|P| �� 13 �ξ�硢ñ���ٳ�ĥ�ե����ޥåȤ���Ѥ��뤳�Ȥˤ�ꡢ9 ��� 10 �ʿ����Ǥ�ᤤ 2 �ʿ����Ѵ� (���ʤ�����Τʴݤ�) ����뤳�Ȥˤʤ�ޤ����ޤ� |P| > 13 �ξ�硢ñ���ٳ�ĥ�ե����ޥåȤǤϾ�Υ��르�ꥺ��˽�ʬ�б��Ǥ��ʤ��Τǡ�ɬ���������Τ� 2 �ʿ������Ǥ���Ȥϸ¤�ޤ������� Coonen (1984) �ˤ�ꡢ2 �ʿ����� 10 �ʿ��ؤ��Ѵ��ȡ����εդ����ǡ���Ȥ� 2 �ʿ�����������뤳�Ȥ��¾ڤ���Ƥ��ޤ���
�����٤����ݡ��Ȥ���Ƥ���С��嵭�Υ��르�ꥺ��ϳ�ĥñ���٥ե����ޥåȤǤϤʤ������٤Ǽ¹Ԥ���ޤ����������������٥ե����ޥåȤ� 17 ��� 10 �ʿ����Ѵ����������᤹���ˤϳ�ĥ�����٥ե����ޥåȤ�ɬ�פˤʤ�ޤ���
�ؿ�
�ؿ��ˤ�������� 2 �Ĥδط����ͤ�����Τǡ�����ɽ�����뤿����������ˡ�����ʤ���Фʤ�ޤ�������դ��ο��ϡ����ȿ��̤��Ȥ߹�碌����ˡ�ȡ�2 �������ɽ��������ˡ������ޤ������/���̤η����ϡ�IEEE �ե����ޥåȤˤ��ͭ�շ������ɽ�魯���˻��Ѥ���ޤ������ʤ�� 1 �ӥåȤ�����ѤȤ��Ƴ��ݤ����Ĥ�ΥӥåȤǿ��̤�ɽ�路�ޤ����ޤ� 2 �������ɽ�魯��ˡ�������黻�ΤȤ��ˤ褯���Ѥ���ޤ���������ˡ�Ǥϡ�[ -2p-1 , 2p-1 - 1] ���ϰϤˤ������ 2p �ξ�;��������������κǾ��ͤ�ɽ�魯���Ȥ��Ǥ��ޤ���
IEEE 2 �ʿ�ɸ��ǻؿ���ɽ��������ϡ����������ˡ����Ѥ��ޤ�������ˡ��Х�����ɽ���פ���Ѥ��ޤ����ؿ��� 8 �ӥåȤdz�Ǽ����ñ���٤ξ�硢�Х������� 127 �Ȥʤ�ޤ� (�����٤ξ��� 1023 �Ǥ�)��
�����ʤ���������ɽ�魯�ؿ��ӥåȤǤ����硢��ư���������λؿ���
- 127 �ˤʤ�ޤ�������ϥХ������ؿ�
�ȶ��̤��뤿��ˡ��֥Х������ʤ��λؿ��פȸƤФ�뤳�Ȥ�����ޤ���
ɽ D-1 ��ȡ�ñ���٤ξ��� emax = 127��emin = -126 �Ǥ��뤳�Ȥ��狼��ޤ���|emin |< emax �Ȥʤ�Τϡ��Ǿ���
�εտ��������С��ե������ʤ��Ȥ�����ͳ�ˤ���ΤǤ��������ͤεտ�����������ե������뤳�ȤϤ���ޤ���������ϥ����С��ե����ξ��ۤɿ��������ǤϤ���ޤ����ִ�����Ǥϡ�0 ��ɽ�魯�Τ� emin - 1����Ѥ�����������ޤ������ޤ� ���ü�ʿ����Ǥϡ�emax + 1 �ˤĤ����������ޤ���IEEE ñ���٤ξ�硢����ϥХ������ؿ����ϰϤ�
emin - 1 = 127 ���� emax + 1 = 128 �ˤ���Ȥ������Ȥˤʤ�ޤ����������Х������ʤ��λؿ����ϰϤϡ�0 ���� 255 �ޤǤȤʤꡢ8 �ӥåȤ�ɽ���Ǥ�������ο����������ޤ������
IEEE ɸ��Ǥϡ���§�黻�η�̤����Τ˴ݤ���ޤ������ʤ����̤����Τ˷������塢�Ǥ�ᤤ��ư���������˴ݤ�� (�����ؤδݤ�) �Ȥ������ȤǤ������ݸ����Ǥϡ����Τʺ��� 2 �Ĥ���ư�����������¤������Τϡ��ؿ����礭���ۤʤ�Ȥ��˥����ȹ�ˤʤ�Ȼ�Ŧ���ޤ���������ˡ����и�����Ǿ��¤��������ʤ��麹���������������ˡ��Ҳ𤷤ޤ�������������1 ����ݸ�����Ѥ��Ʒ���������Ȥ��äơ�ɬ�����⡢���Τʷ�̤��������Ǵݤ�������Ʊ���η�̤�������Ȥϸ¤�ޤ���
������ 2 ���ܤ��ݸ��� 3 ���ܤ����ƥ��å��ӥåȤ���Ѥ��뤳�Ȥˤ�ꡢ1 ����ݸ��ξ����¿���Υ����Ȥ�ȼ����ΤΡ����Τʷ��θ�˴ݤ��Ԥʤä�����Ʊ����̤����뤳�Ȥ��Ǥ��ޤ� (Goldberg 1990)��������ˡ�ˤ�ꡢɸ������ΨŪ�˼¸��Ǥ��ޤ���
���ѱ黻�η�̤����˻��ꤹ�뤳�Ȥˤ�ꡢ���եȥ������ΰܿ�������������ޤ�������ޥ����̤Υޥ���˥ץ�������ܿ�����Ȥ��ˡ�ξ���Υޥ���� IEEE ɸ�ब���ݡ��Ȥ���Ƥ���С����δ֤������������ַ�̤Ϥ��٤ƥ��եȥ������Х��˸��������ꡢ�黻��κ��ˤ���ΤǤʤ����Ȥ��ο��Ǥ��ޤ����ޤ����Τʻ���ˤ�äơ���ư�������˴ؤ��������Ԥ��䤹���ʤ�ޤ�����ư�������˴ؤ�������ϡ����ޤ��ޤʱ黻�����������ǵ�����Ƽ��������н褹��ɬ�פ��ʤ����Ǥ���������ΤǤ��������ץ�����ब���������Ȥ�����Ǥ���Τ�Ʊ���褦�ˡ���ư�������ץ������ξ��⡢�����������Ƥ�����̤δݤ�����ˤ�ä�����ξ�郎���������Ȥ�����ΤǤ��äƤ⡢�������뤳�Ȥ��Ǥ��ޤ������� 4 �ϡ����Τ褦�ʾ������������ΤǤ����������������ϡ����������������Ƥ����Τ˻���Ǥ���С��Ϥ뤫���ưפˤʤ�ޤ������ä����륢�르�ꥺ�ब IEEE �黻��Ŭ�礷�Ƥ��뤳�Ȥ��狼��С�IEEE ɸ��ݡ��Ȥ���ޥ���Ǥ���¤ꡢ������Ǥ��äƤ�������ư��ޤ���
Brown (1981) �ϡ�����Ū����ư�������ϡ��ɥ������˸����븶����ȯɽ���ޤ����������������Υ����ƥ�Ǥξ�����ɬ�����⡢���껦���� �����Τʴݤ������˼������르�ꥺ������������դ��뤳�ȤˤϤʤ�ޤ������Υ��르�ꥺ������������٤ƤΥϡ��ɥ������ǥ��ݡ��Ȥ���Ƥ���Ȥϸ¤�ʤ�����Ǥ�������ˡ�Brown �θ����ϡ�ñ�����Τʷ��ȴݤ����˴ؤ���ñ���������⡢���ʤ�ʣ���ˤʤäƤ��ޤ����������äơ�Brown �θ������Ȥ�������Ƴ���Τϡ���ñ�����Τʴݤ�Ǥ��뤳�Ȥ�����Ȥ��ƾ���������������ʤ�ޤ���
��ư������ɸ��ˤ�ä��б������������ƤˤĤ��Ƥϡ�����Ū��Ʊ�դ���Ω����Ƥ���櫓�ǤϤ���ޤ���+��-��×��/ �λ�§�黻�ʳ��ˡ�IEEE ɸ��Ǥ�ʿ��������;������/��ư���������Ѵ��γ��������Τ˴ݤ��褦�˵��ꤵ��Ƥ��ޤ����ޤ��������ե����ޥåȤ�10 �ʿ����Ѵ������Τ˴ݤ�ʤ���Фʤ�ޤ��� (���������������礭�����ξ��Ͻ����ޤ�)��Kulisch �� Miranker (1986) �ϡ����Τ˻��ꤵ�줿���Υꥹ�Ȥ����Ѥ��ɲä��뤳�Ȥ���Ƥ��ޤ�����IEEE �黻�ˤ�ȤŤ������Ѥ������ȡ��ǽ�Ū�ʲ��礭���ۤʤ뤳�Ȥ�����Ȼ�Ŧ����Ƥ��ޤ���
�㤨�С��¤����Ѥ��ü�ʥ������ʤΤǡ� ((2 × 10-30 + 1030) - 1030 ) -10-30 ���¤�
10-30��Ʊ���ˤʤ�ޤ��������� IEEE �б��Υޥ���Ǥϡ�����̤� -10-30 �Ȥʤ�ޤ�����®�ξ軻���¸������꾯�ʤ��ϡ��ɥ����������Ȥǡ������� 1 ulp ������ޤ������Ѥ�����뤳�Ȥ��Ǥ��ޤ� (Kirchner/Kulish��1987)��14 15ɸ��Ȥ��Ƶ��ꤵ������Ϥ��٤ơ�10 �ʿ��� 2 �ʿ����Ѵ������ξ�����������Τ˴ݤ��Ԥ�ɬ�פ�����ޤ�������ϡ��Ѵ���������������٤Ƥ����ˤĤ������Τ˴ݤ�����ΨŪ�ʥ��르�ꥺ�ब�¾ڤ���Ƥ��뤫��Ǥ����ʤ��Ѵ������ξ��ϡ��Ǥ����Ū�Ǥ���Ȥ���륢�르�ꥺ��Ǥ⡢���Τʴݤ�ˤ�������١�¿�����٤�����ޤ� (Coonen��1984) ��
IEEE ɸ��Ǥϡ����ơ��֥롦����Υ������פ����뤿��ˡ�Ķ�۴ؿ���ɬ���������Τ˴ݤ��ɬ�פϤ���ޤ�������������뤿��ˡ�4 �Ĥξ������ΰ��֤ǻؿ��ؿ��Υơ��֥������������ͤ��Ƥߤޤ���exp (1.626) = 5.0835 �Ȥ��ޤ��������ݤ��ȡ�5.083���ޤ��� 5.084 �Τ�����ˤʤ�ΤǤ��礦��exp (1.626) �Ť˷�����ȡ�5.08350 �Ȥʤ�ޤ�������� 5.083500������ 5.0835000 �ˤʤ�ޤ���exp ��Ķ�۴ؿ��Ǥ����硢exp (1.626) �� 5.083500 ...0ddd���ޤ��� 5.0834999 ...9ddd �Τ�����Ǥ��뤫��Ƚ�ǤǤ���ޤǤ��������֤��������ǽ��������ޤ����������äơ�Ķ�۴ؿ��ˤĤ��ơ�̵��������٤Ƿ������塢���η�̤�ݤ����Ʊ���褦�����٤����Τϸ���Ū�ǤϤ���ޤ����̤Υ��ץ������Ȥ��ơ�Ķ�۴ؿ��르�ꥺ��Ū�˻��ꤹ�뤳�Ȥ�Ǥ��ޤ��������������٤ƤΥϡ��ɥ������������ƥ������Ŭ�ѤǤ��� 1 �ĤΥ��르�ꥺ�ब¸�ߤ���櫓�ǤϤ���ޤ��Ƕ�Υޥ����Ķ�۴ؿ����������ˡ�ͭ������͡�CORDIC16��������緿�ơ��֥�Ȥ��� 3 �Ĥμ�ˡ����ѤǤ��ޤ���������μ�ˡ�⤽�줾���ȼ��Υ��饹�Υϡ��ɥ�������Ŭ�Ѥ�����Τǡ����ߤΤȤ������Ƽ�Υϡ��ɥ��������������б��Ǥ���ñ��Υ��르�ꥺ��Ϥ���ޤ���
�ü�ʿ�
��ư�������ϡ��ɥ������ˤ�äƤϡ��ƥӥåȥѥ�����ͭ������ư����������ɽ�魯��礬����ޤ���IBM System/370 �ϡ����ΰ���Ǥ���������VAXTM �Ǥϡ���ͽ�ڥ����פȤ����ü�ʿ���ɽ�魯����Υӥåȥѥ������ݤ���Ƥ��ޤ������ιͤ����� CDC 6600 ��ͳ�褹���Τǡ�
INDEFINITE��INFINITY�Ȥ����ü�ʿ��Υӥåȥѥ������Ѥ���ޤ���IEEE ɸ��ˤϡ�����������Ѿ����ơ�NaN (Not a Number ) ��̵����Ȥ�����ǰ������ޤ����ü�ʿ������ݡ��Ȥ���Ƥ��ʤ��ȡ������ʿ�����ʤɤ��㳰��������������硢���ܡ��Ȥ���ʳ����н褹����ˡ������ޤ���IBM System/370 FORTRAN �Ǥϡ�-4 �Τ褦�������ʿ�����η��˽вȡ��ǥե���Ȥ�ư��Ȥ��ƥ��顼��å���������Ϥ��ޤ����ƥӥåȥѥ�����ϡ�ͭ���ʿ���ɽ�魯�Τǡ�ʿ����������ͤ���ư���������Ǥʤ���Фʤ�ޤ���System/370 FORTRAN �ξ��
���ᤵ��ޤ���������IEEE �黻�ξ��ϡ�NaN ���ᤵ��ޤ���
IEEE ɸ��ˤ�ꡢ�����ü���ͤ����ꤵ��ޤ� (ɽ D-2 �Ȥ��Ƥ�������)����0����������������
������� NaN (���ι����������Ȥ��ꡢNaN ��¸�ߤ��ޤ�) �Ǥ����������ü���ͤϡ�emax + 1 �ޤ��� emin - 1 �λؿ��ˤ�äƤ��٤ƥ����ɤ���ޤ� (�ʤ���0 �ˤ� emin - 1 �λؿ������뤳�ȤϤ��Ǥ˻�Ŧ�����Ȥ���Ǥ�)��
ɽ D-2 IEEE 754 ���ü���� e = emin - 1 f = 0 ��0 e = emin - 1 f �� 0 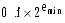
emin �� e ��emax -- 1.f × 2e e = emax + 1 f = 0 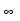
e = emax + 1 f �� 0 NaN
NaNs����ޤǡ�0/0 ��
�ʤɤη��ϡ����λ����Ƿ�����ߤθ����Ȥʤ������ǽ�ʥ��顼�Ȥ��ư����Ƥ��ޤ��������������������������Ǥ���Τޤ�³�Ԥ��뤳�Ȥ˰�̣�����륱������ͤ����ޤ������Ȥ��С�����ؿ�
f�Υ�������륵�֥롼����zero(f)�����ͤ��Ƥߤޤ������衢�������Х��֥롼��������Ԥ����֤Ȥ��ơ��ؿ���������줿�ֳ� [a,b] ��桼���������ꤷ�ʤ���Фʤ�ޤ���Ǥ��������Υ��֥롼����Τ��Ȥ�zero(f,a,b)�ȸ����ޤ�������������ʥ������Х��֥롼����Ǥϡ������ɲþ�������Ϥ���ɬ�פϤ���ޤ���������Ū�ʥ������Х��֥롼����ϡ�ñ�˴ؿ������Ϥ������ᤵ�졢�ΰ�λ���ʤɤ�̵��̣�Ȥʤ�褦������ʤɤ�Ŭ�ѤǤ��ޤ������������ºݤˤϤۤȤ�ɤΥ������Х��֥롼������ΰ�λ��꤬ɬ�פˤʤ�ޤ���������ͳ�ϴ�ñ�Ǥ����������Х��֥롼����Ϥ����Ĥ����ͤǴؿ�f��Ĵ�٤뤳�Ȥˤ�������Ԥ��ޤ���f���ΰ��Ķ�����ͤ�����ȡ�f���Ф��륳���ɤ� 0/0 �ޤ����ˤʤꡢ������ߤ��ơ��������Хץ������ܡ��Ȥ��Ƥ��ޤ����Ȥ����뤫��Ǥ���
��������ϡ�NaN �Ȥ����ü���ͤ�Ƴ������0/0 ��
�μ��η��Ǥϡ���������ߤ�������� NaN ����������褦�˻��ꤹ��С���褷�ޤ���ɽ D-3 �ˤϡ�NaN �θ����Ȥʤ�������Ĥ������Ƥ���ޤ���
zero(f)��f���ΰ��Ķ�����ͤ�����ȡ�f�Υ����ɤˤ�� NaN ���֤��졢�������Х��֥롼����ν�����³�Ԥ��ޤ������ʤ����zero(f)�ϸ��ä���¬�����ȤˤĤ��ơ֤Ȥ������פ��ȤϤ���ޤ���������Ȥˡ�NaN ���̾����ư�����������Ȥ߹�碌�����η�̤��ñ�˳�ǧ���뤳�Ȥ��Ǥ��ޤ���f�κǸ��ʸ��return (-b + sqrt(d))/(2*a)�Ȥʤ�ޤ���d < 0 �ξ�硢f�� NaN ���֤��ޤ���d < 0 �ʤΤǡ�NaN ���̤ο����¤� NaN �ξ��ϡ�sqrt(d)�� NaN��-b + sqrt(d)�� NaN �ˤʤ�ޤ���Ʊ�ͤˡ������Τ����줫�Υ��ڥ��ɤ� NaN �ξ�硢���� NaN �ˤʤ�ޤ������̤ˡ���ư���������� NaN ���ᤵ�줿���ϡ���̤� NaN �ˤʤ�ޤ���
ɽ D-3 NaN �������������� + + (-
)
x 0 x 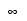
/ 0/0, /
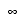
REM x REM0,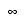
REMy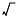
(x < 0 �ΤȤ�)
�桼�������ΰ�����Ϥ���ɬ�פΤʤ�����������Ф���������̤Υ��ץ������Ȥ��ơ������ʥ����Ѥ��뤳�Ȥ�Ǥ��ޤ����������Х��֥롼����ϡ���ư�������㳰���Ф��륷���ʥ�ϥ�ɥ�ȡ��뤹�뤳�Ȥ��Ǥ��ޤ���
f���ΰ賰��ɾ�����졢�㳰��ȯ������ȡ�����ϥ���������Ф��Ϥ���ޤ������Υ��ץ��������������ϡ��Ƹ��줴�Ȥ˥����ʥ�����������ˡ���ۤʤ� (������ˡ���ʤ����⤢��ޤ�) �Τǡ��ܿ������ޤä����ʤ��Ȥ������Ǥ���IEEE 754 �Ǥϡ�NaN �ϻؿ� emax + 1 �ȥ����ʳ���ͭ�շ��ȼ����ư���������Ȥ���ɽ�魯���Ȥ�����ޤ����������Ȥˡ������ƥ��¸�ξ����ͭ�շ������뤳�Ȥ��Ǥ��ޤ����������äơ���դ� NaN ��¸�ߤ���櫓�ǤϤʤ�����Ϣ�� NaN �����Τ���������뤳�Ȥˤʤ�ޤ���NaN ���̾����ư�����������Ȥ߹�碌��ȡ���̤� NaN ���ڥ��ɤ�Ʊ���ˤʤ�ޤ����������äơ�Ĺ�����η�̤� NaN �ξ�硢ͭ�շ�ˤ��륷���ƥ��¸�ξ���ϡ��ǽ�� NaN ���������줿������������������Ȥʤ�ޤ����ºݤˡ��Ǹ��ʸ�ˤ����դ�ɬ�פǤ���ξ���Υ��ڥ��ɤ� NaN �ξ�硢��̤Ϥ����줫������ NaN �ˤʤ�Τǡ�ɬ������ǽ���������줿 NaN �Ǥ���Ȥϸ¤�ޤ���
̵����
NaN����Ѥ��ơ�0/0 ���Τ褦�ʼ������Ф��줿�Ȥ��˷���³�Ԥ��������Ʊ���褦�ˡ�̵����ˤ�äƥ����С��ե������������Ȥ��˽�����³���뤳�Ȥ��Ǥ��ޤ��������ñ�˺�����ƿ����᤹���⡢�Ϥ뤫�˰�������ˡ�Ǥ���
�㤨�С���= 10�� p = 3��emax = 98 �ΤȤ�����ͤ��Ƥߤޤ���x = 3 × 1070��y = 4 × 1070 �ξ�硢x2 �ϥ����С��ե�������9.99 × 1098 ���֤��������ޤ���Ʊ���褦�ˡ�y2������� x2 + y2 �Ϥ��줾���˥����С��ե������ơ�9.99 × 1098 ���֤��������ޤ����ǽ�Ū�ˤϡ�
�Ȥʤꡢ����� 5 × 1070 �ȤϤۤɱ�̤Ȥʤ�ޤ���IEEE �黻�ξ�硢x2 �η�̤ϡ�y2 ��x2 + y2 ��
��Ʊ���褦�ˡ�
�Ȥʤ�ޤ����ǽ�Ū�ʷ�̤�
�Ȥʤꡢ��������������礭���Ϥ��줿�̾����ư�����������᤹��ꡢ�Ϥ뤫�˰����Ǥ���ȸ����ޤ�17��
0 �� 0 �ǽ������Ƥ⡢NaN �ˤʤ�ޤ��������ʳ��ο��� 0 �dz��ȡ�
���֤���ޤ� (1/0 =
��-1/0 = -
)���������̤�����ͳ�ϼ��ΤȤ���Ǥ���x ������³����᤹ܶ��˽�����f(x) �� 0��g(x) �� 0 �ˤʤ��硢f(x)/g(x) ���ͤ�Ǥ�դˤʤ�ޤ����㤨�С�f(x) = sin x��g(x) = x �ξ�硢x �� 0 ���� f(x)/g(x) �� 1 �Ǥ�����f(x) = 1- cos x �ξ�硢f(x)/g(x) �� 0 �ˤʤ�ޤ���0/0 ��2 �Ĥξ������ͤξ������¤�����Ȥ���ª����ȡ�0/0 ��Ǥ�դˤʤ�ޤ����������äơ�IEEE ɸ��ǡ�0/0 ��
NaN�ˤʤ�ޤ�����������c > 0 �ξ�硢f(x) �� c��g(x) �� 0 �Ǥ���С�������ʬ�ϴؿ� f �� g �ˤĤ��� f(x)/g(x) �����Ȥʤ�ޤ��������� x ���Ф��� g(x) < 0 �ξ�硢f(x)/g(x) ��-
�Ȥʤ�ޤ�������ʳ��ξ��ϡ��³��� +
�ˤʤ�ޤ����������äơ�IEEE ɸ��Ǥϡ�c �� 0�Ǥ���¤ꡢc/0 =��
���������ޤ���
�����ϡ��̾�� c �� 0 �����˰�¸����Τǡ�-10/0 = -
���ޤ� -10/-0 = +
�Ȥʤ�ޤ��������С��ե��������������������
�ȡ������ˤ������������ǵ�����
�Ȥΰ㤤�ϡ����ơ������ե饰������å�����ж��̤Ǥ��ޤ� (�ܺ٤ˤĤ��Ƥϡ��֥ե饰�����������Ƥ���
�� ) �����Ԥξ��ϥ����С��ե������ե饰�����ޤ���Ԥξ��ϥ����ˤ������Υե饰�����줾�쥻�åȤ���ޤ������ڥ��ɤȤ���̵����������������η�̤���ꤹ��롼��ϴ�ñ�Ǥ���
̵�����ͭ�¿� x ���֤����������θ³��� x �������ꤷ�ޤ���
�������äơ��ʤΤǡ�3/
= 0 �ˤʤ�ޤ���
Ʊ�ͤˡ�4 -
= -
��
=
�ˤʤ�ޤ����³����ʤ���硢��̤� NaN �ˤʤ�Τǡ�
/
�� NaN �ˤʤ�ޤ� (ɽ D-3���ɲä�����Ƥ��ޤ�)������ϡ�0/0 �� NaN �ˤʤ�ȷ���������ο����Ȱ��פ��ޤ���
������ʬ����
NaN��ɾ�������ȡ������Τ��ͤ�NaN�ˤʤ�ޤ��������������ξ�硢1/
= 0 �Τ褦�ʥ롼�뤬����Τǡ������ͤ��̾����ư���������ˤʤ��礬����ޤ��������Ǥϡ�̵����α黻�ˤĤ��ƥ롼���Ŭ�Ѥ���ºݤ�����ޤ���
�ؿ� x/(x2 + 1) ����������ͤ��Ƥߤޤ�������ϡ�x ��
����礭���ʤ�ȥ����С��ե�������Τǡ��褤�����ǤϤ���ޤ���̵����η��ˤ�ꡢ1/x �ζ���ͤǤϤʤ� 0 �����������Τǡ����ä��������ޤ��������� x/(x2 + 1) �� 1/(x + x-1) �Ƚ����뤳�Ȥ��Ǥ��ޤ������ν����ˤ�ꡢ�ᤤ�ʳ��ǥ����С��ե����������뤳�ȤϤʤ��ʤꡢ̵����α黻�ˤ�ꡢx = 0 : 1/(0 + 0-1) = 1/(0 +
) = 1/
= 0 �ΤȤ����������ͤ������ޤ���̵����α黻���ʤ��ȡ�1/(x + x-1) �μ��Ǥϡ�x = 0 ���ɤ�����ƥ��Ȥ���ɬ�פ�����ޤ������ξ�硢;ʬ��̿��ɲä����ۤ����ѥ��ץ饤���˲�������ǽ��������ޤ���������ϡ�̵����α黻�ˤ�äơ��ü�ʥ�����������å�����ɬ�פ��ʤ��ʤ�Ȥ�������Ū�ʻ��������ΤǤ��������������ˤĤ��Ƥϡ�̵������ˡ�����Ū��ư�� (x/(x2 + 1) �Τ褦��) �����Ȥ��ʤ��褦�ˡ����Ť�Ĵ�٤�ɬ�פ�����ޤ���
����դ�����
�����ϡ��ؿ� emin -1 �ȥ�����ͭ�շ�ˤ�ä�ɽ�魯���Ȥ��Ǥ��ޤ������ӥåȤ� 2 �Ĥ��ͤ��뤳�Ȥ��Ǥ���Τǡ������ˤ� +0�� -0 �� 2 ���ब����ޤ���+0 �� -0 ����Ӥ�����ˡ����̤��Ƥ��ޤ��ȡ�
if(x=0)�Τ褦�ʴ�ñ�ʥƥ��ȤǤ⡢x�����ˤ�ä�ͽ¬�Ǥ��ʤ���̤ˤʤ뤳�Ȥ�����ޤ����������äơ�IEEE ɸ��Ǥϡ�-0 < +0 �ǤϤʤ���-0 = +0 �Ȥʤ�褦���������Ƥ��ޤ�������������Ĥͤ�̵�뤹�뤳�Ȥ��ǽ�Ǥ�����IEEE ɸ��Ǥ�̵�뤵��ޤ��軻���ޤ��Ͻ���������դ��Υ�����ȼ����硢������������Ȥ��ˤ��̾����椬Ŭ�Ѥ���ޤ����������äơ�3·(+0) = +0������� +0/-3 = -0�ˤʤ�ޤ����ޤ���������椬�ʤ����ϡ�x =���ξ�硢1/(1/x) = x ������Ω���ʤ��ʤ�ޤ���������ͳ�� 1/-
�� 1/+
�Ϥ������ 0��1/0 �� +
�Ȥʤꡢ���������뤫��Ǥ���1/(1/x) = x �ΰ�̣���ݻ�����ˤϡ�������̵�����������Ѥ��ޤ������������ξ��⡢�����С��ե�������������椬������Ȥ�����̤��Ѥ��ޤ���
����դ���������Ѥ���⤦ 1 �Ĥ���ϡ���������ե����ȡ�log �Τ褦�� 0 ����Ϣ³�Ȥʤ�ؿ��˴ؤ����ΤǤ���IEEE �黻�Ǥϡ�x < 0 �ΤȤ��ˡ�log 0 = -
��log x �� NaN ���������Τ������ˤʤäƤ��ޤ��������˥�������ե������������������ɽ�魯 x �����ͤ��Ƥߤޤ�������դ��Υ����Τ���ˡ�x ������ˤʤ�Τǡ�log ��
NaN���᤹���Ȥ��Ǥ��ޤ��������������ʤ��Υ����ξ�硢log �ؿ��ϥ�������ե������������ 0 �Ȥ���̤Ǥ��ʤ��ʤ�Τǡ�-���֤��ޤ�����������Ϣ³�ˤʤ�⤦ 1 �Ĥδؿ�����Ȥ��ơ����ͤ������֤� signum �ؿ�������ޤ���
����դ������κǤⶽ̣�Τ�����ϡ�ʣ�ǿ��黻�Ǥ���
ñ�����Ȥ��ơ�
�Ȥ�����������ͤ��Ƥߤޤ�������ϡ�z � 0�ξ��˿��ˤʤ�ޤ���
z = -1 �ξ��ϡ�
�������
�Ȥʤ�ޤ���
�������äơ�
�Ȥʤ�ޤ�����������ϡ�ʿ������ʣ�����ͤȤʤꡢʣ�ǿ�ʿ�����Τ�Ϣ³�����ͤ�����Ǥ��ʤ��Ȥ������¤�ͳ�褹���ΤǤ��������������٤���μ¿��ǹ��������֥������åȤ��θ���оݤ��鳰���С�ʿ������Ϣ³�ˤʤ�ޤ�������Ǥ⡢-x + i0 (������ x > 0) �η�������μ¿��ˤĤ��ơ��ɤ��������Ȥ�������ϻĤ�ޤ�������դ������ˤ�ꡢ������������ʷ��Dz�褹�뤳�Ȥ��Ǥ��ޤ���
x + i(+0) �η����ο����������ޤ��֥������åȤΤ⤦�����ˤ��� x + i(-0) �η����ο��ϡ��դ�����
�ˤʤ�ޤ����ºݤˡ�
�����������ˤ�ꡢ���η�̤������ޤ���
�Ȥʤ�Τǡ�z = -1 + i0 �Ǥ���С�
1/z = 1/(-1 + i0) = [(-1 - i0)] / [(-1 + i0)(-1 - i0)] = (-1 - i0)/((-1)2 - 02 ) = -1 + i(-0)
�Ȥʤꡢ������
�Ȥʤ�ޤ���
�������äơ�IEEE �黻�Ǥϡ����٤Ƥ� z �ΰ�̣���ݻ�����ޤ�������˹��٤��㤬 Kahan �ˤ�äƾҲ𤵤�Ƥ��ޤ� (1987)��+0 �� -0 ����̤��뤳�Ȥ������Ϥ���ޤ������狼��ˤ����ʤ뤳�Ȥ�����ޤ����㤨�С�����դ������ˤ�ꡢx = +0������� y = -0 �ΤȤ��˵��Ȥʤ� x = y �� 1/x = 1/y �δط�������ޤ�����������IEEE �Ѱ���Ǥϡ�����դ���������Ѥ�������������������������äƤ����Ƚ�Ǥ��Ƥ��ޤ�������������
��= 10�� p = 3��emin = -98 �����������줿��ư�������������ͤ��Ƥߤޤ���
x = 6.87 × 10-97 �� y = 6.81 × 10-97 �ϡ��Ǿ�����ư�������� 1.00 × 10-98 �� 10 �ܰʾ��礭���Τǡ��̾����ư���������Τ褦�˻פ��ޤ�������������������ư���������ˤϡ�x �� y! �Ǥ��äƤ⡢xy = 0 �ˤʤ�Ȥ����Ѥ�ä�����������ޤ���
����ϡ�x - y = 0.06 × 10-97 = 6.0 × 10-99 �������������Ȥ��ƤϾ���������ɽ���Ǥ��ʤ����ᡢ�����˥ե�å��夷�ʤ���Фʤ�ʤ��Ȥ�����ͳ�ˤ���ΤǤ��������������ݻ����뤳�Ȥϡ��ɤ����ٽ��פʤΤǤ��礦��
if (x��y) then z=1/(x-y)�Ȥ��������ɡ��ե饰���ȤҤ�����ǡ���������Υ��������ˤ�äƥץ������ܡ��Ȥ����뤳�Ȥ��ñ�ˤǤ��ޤ��������������Τ褦�ʥХ����Ф���ˡ�ϡ�����Ū�ˤ����Ū�ˤ��礭����ô�ˤʤ�ޤ�������˹��٤���ˡ�Ȥ��ơ�����ԥ塼���������λ��ͽ�ˤϡ����ߤΤȤ����絬�Ϥʥץ��������������ڤ���Τϸ���Ū�ǤϤʤ���ΤΡ������¾ڤ��뤳�Ȥ�ǰƬ�˥ץ��������߷פ���ȡ���ΨŪ�ʥ����ɤ��Ǥ�������Ȼ�Ŧ����Ƥ��ޤ����㤨�С����Ѽ����������Τϡ����ˤ��줬�����ΰ����Ȥ��Ƥ����ѤǤ��ʤ����Ǥ⡢����Ū�ʼ��ʤǤ�����ư�����������ɤˤ�äơ��̾�Υ����ɤξ���Ʊ���褦�ˡ�����Ǥ��������ǽ�ʻ��¤�������褦�ˤʤ�ޤ���
�㤨�С����� (6) ��ʬ�Ϥ����硢x/2 < y < 2xx
y = x - y �Ȥ������¤��狼���������Ω���ޤ���Ʊ���褦�ˡ����� (10) �����Ǥ��뤳�Ȥ��狼��С�����Ǥ�����ư�����������ɤ�Ҥ��䤹���ʤ�ޤ�������ʬ�ο��ˤ��ƤϤޤ뤫��Ȥ�������ϡ�����������뤳�ȤˤϤʤ�ޤ���
IEEE ɸ��Ǥϡ���������18������Ѥ��Ƹ��� (10) ������Ӥ���¾�δط���������ޤ��������������Ϥ褯�������оݤȤʤ���ʬ�Ǥ��ꡢ754 ��ǧ�Ĥ����ޤǤ�Ĺ�����֤������ä��Τϡ������餯������ͳ�ˤ���ΤȻפ��ޤ����ѥե����ޥι⤤�ϡ��ɥ������ϤۤȤ�ɤξ�硢IEEE �ߴ��Ǥ��뤳�Ȥ����ʤ����������������ľ�ܥ��ݡ��Ȥ��뤳�ȤȤϸ¤�ޤ�����������������ѡ����뤤��������������ǥϡ��ɥ��������ȥ�åפ��졢���եȥ������� IEEE ɸ��Υ��ߥ�졼�������Ǥ��������ˤʤäƤ��ޤ�19���������������طʤˤ���ͤ��ϡ�Goldberg (1967) ����Ƥ�����Τǡ�������ñ��Ǥ����ؿ��� emin �ξ�硢ͭ�շ������������ɬ�פ��ʤ��Τǡ���= 10�� p = 3��emin = -98 �Ǥ���С�0.98 × 10-98 ����ư���������ˤʤ�Τǡ�1.00 × 10-98 �ϺǾ�����ư���������ǤϤʤ��ʤ�ޤ���
��= 2 �ξ��˱���ӥåȤ���Ѥ���ȡ�emin �λؿ���ȼ�����ϡ����ۤ���Ԥ���ӥåȤ����뤿���ɬ��ͭ�շ夬 1.0 �ʾ�ˤʤ�Τǡ�¿���λپ㤬�ФƤ��ޤ������β����ˡ�ϡ�0 ��ɽ�魯���Τ����Ʊ���ǡ�ɽ D-2 �ˤޤȤ�Ƥ���ޤ���emin �ؿ�����Ѥ��ơ�������������ɽ�魯���Ȥ��Ǥ��ޤ������ʤ��ͭ�շ�ե�����ɤΥӥåȤ� b 1, b 2, ... b p -1�ǡ��ؿ����ͤ� e �ξ�硢ɽ��������� 1.b 1b 2 ... bp -1 × 2e �Ȥʤꡢe = emin -1 �ξ��� 0·b 1b 2 ... b p -1 × 2e+1 �Ȥʤ�ޤ��������������ˤ� emin -1 �ǤϤʤ���emin �λؿ���ȼ���Τǡ��ؿ��� +1 ��ɬ�ܤˤʤ�ޤ���
�ܹ�κǽ�˼�������= 10�� p =3��emin = -98��x = 6.87 × 10-97��y = 6.81 × 10-97 �����ƤӼ��夲�ޤ��������������ξ�硢x - y �ϥ����ؤΥե�å���ϹԤ�줺������� 0·6 × 10-98 �Ȥ���������������ɽ�蘆��ޤ�������ư��Τ��Ȥ��ʳ�Ū�ʡ֥�������ե����פȸ����ޤ����ʳ�Ū��������ե�������Ѥ���С����� (10) ���Ĥͤ˿��ˤʤ뤳�Ȥ��ñ�˸��ڤ��뤳�Ȥ��Ǥ��ޤ���
�� D-2 �ʳ�Ū��������ե����ȥ����ե�å�������
�� D-2 �ˡ��������������ޤ�����ο����ϡ�������������ư����������ɽ�路�ޤ���0 ����Ǿ����������� 1.0 ×
�ޤǤ˳ʺ������뤳�Ȥ����դ��Ƥ�����������ư�������黻�η�̤����κ����ϰϤ�������ϡ������ؤΥե�å��夬�Ԥ��ޤ������ο����ϡ���Ϣ����ư����������������������ä����Ȥ��ˡ��ɤ���������뤫������ΤǤ������γʺ�������졢����̤� 1.0 ×
��꾯�ʤ���С��Ǥ�ᤤ������������ɽ�蘆��ޤ���������������������û�����ȡ����ܤ�����ư���������ɤ����δֳ֤���§Ū�˼���ޤ������ܤ�����ɤ����δֳ֤�Ʊ�����ȡ��¤η����ˤ�äưۤʤ���Ȥ�����ޤ����������������ʤ���С���-p+1
����
�ޤǤδֳ֤����¤η����ˤ�뵬§Ū���Ѳ��ǤϤʤ�����p-1 �η����˽��äơ�����Ѳ����뤳�Ȥˤʤ�ޤ������Τ��ᡢ��������ե����θ³��˶ᤤ�����������Ф����礭�����и�����ȼ�����르�ꥺ��ϤۤȤ�ɤξ�硢�ʳ�Ū��������ե�������Ѥ���ȡ������ϰ����������ư���褦�ˤʤ�ޤ���
�ʳ�Ū��������ե������ʤ���С�x - y �Τ褦��ñ��ʼ��Ǥ⡢���
x = 6.87 × 10-97������� y = 6.81 × 10-97 ����Τ褦�ˡ����������줿���Ϥ��Ф��������礭�����и�����ȼ�����Ȥˤʤ�ޤ����礭�����и����ϡ������� (Demmel��1984) �˼����褦�ˡ��껦���ʤ����Ǥⵯ�����ǽ��������ޤ���a + ib �� c + id �Ȥ��� 2 �Ĥ�ʣ�ǿ�������������ͤ��Ƥߤޤ������θ����ˤϡ�ʬ�� c + id �Τ����줫�����Ǥ�����礭���Ȥ��ˡ��ǽ���̤��ϰ���ˤ��äƤ⡢�����С��ե�������Ȥ������꤬����ޤ���
� i
���ξ���������硢���� Smith �θ�������Ѥ���ȡ�������Ū�Ǥ���
Smith �θ����� (2��10-98 + i10-98 ) / (4��10-98 + i(2��10-98)) ��Ŭ�Ѥ���ȡ��ʳ�Ū��������ե����ˤ�ä� 0.5 �Ȥ����������������ޤ����������ե�å���ξ��ϡ�
0.4 �ˤʤꡢ������ 100 ulp �Ȥʤ�ޤ�������ϡ�1.0 ×�¤Ȥ�������θ����ϰϤ��ݾڤ��������������Ȥ��Ƥ�ŵ��Ū���ͤǤ���
�㳰���ե饰���ȥ�åץϥ�ɥ�
IEEE �黻�ǡ������ˤ����������뤤�ϥ����С��ե����Ȥ��ä��㳰��������ȡ��ǥե���ȤȤ��Ʒ�̤���𤷡�������³�Ԥ��ޤ�������Ū�ʥǥե���ȤȤ��ơ�0/0 ��
�ˤ� NaN���ޤ� 1/0 �ȥ����С��ե����ˤ�
���֤��ޤ������ι�Ǥϡ��㳰�����������Ǥ⡢�ʾ�Υǥե�����ͤˤ�äƽ�����³�Ԥ�������˾�ޤ�������Ĥ��Ҳ𤷤ޤ����������줫���㳰��������ȡ����ơ������ե饰�⥻�åȤ���ޤ���IEEE ɸ��λ��ͤǤϡ��桼���������ơ������ե饰���ɤ��/���ߤǤ�����ʤ����ʤ���Фʤ�ޤ��ե饰�ϡ����ä��åȤ����ȡ�����Ū�˥��ꥢ�����ʤ��¤ꡢ���Τޤޥ��åȾ��֤ˤʤ�Ȥ�����̣�ǡ֥��ƥ��å��פ�����������ޤ��������̵�����ɽ�魯 1/0 �ȡ������С��ե����Ȥΰ㤤����̤���ˤϡ��ե饰��ƥ��Ȥ���ʳ�����ˡ�Ϥ���ޤ���
�㳰���������Ȥ��ˡ�������³�Ԥ��뤳�Ȥ������Ǥʤ����⤢��ޤ�����̵������Ǥϡ�x/ (x2 +1) ������ޤ�����
x >
�ξ�硢ʬ���̵����ˤʤ�Τǡ��ǽ�Ū�ʲ� 0 �Ȥ������ޤä������ä���̤ˤʤ�ޤ������θ����ξ�硢1/ (x + x-1) �Ƚ����������ϲ�褷�ޤ��������ν����ˤ�ä�ɬ���������꤬��褷�ʤ����⤢��ޤ���IEEE ɸ��Ǥϡ��ȥ�åץϥ�ɥ�ȡ���Ǥ���褦�ʻ��ͤ������侩����Ƥ��ޤ����㳰��������ȡ��ե饰�åȤ�������˥ȥ�åץϥ�ɥ餬�ƤӽФ��졢�ȥ�åץϥ�ɥ餬�֤��ͤ����η�̤Ȥ��ƻ��Ѥ��ޤ������ơ������ե饰�ꥢ���ޤ��ϥ��åȤ���Ȥ���Ƚ�Ǥϡ��ȥ�åץϥ�ɥ�˰�Ǥ����ޤ�������ʳ��ξ�硢�ե饰���ͤ�̤����ˤ��뤳�Ȥ��Ǥ��ޤ���
IEEE ɸ��Ǥϡ��㳰�μ���ˤ�äơ������С��ե�������������ե����������ˤ�������̵����������������Τ����Ȥ��� 5 �ĤΥ��饹��ʬ�ष�Ƥ��ޤ����㳰�γƥ��饹���Ȥˡ����̤Υ��ơ������ե饰���Ѱդ���Ƥ��ޤ����ǽ�� 3 �Ĥ��㳰�ΰ�̣�Ϥ���̾�������Ȥ���Ǥ���̵�������Ȥϡ�ɽ D-3 �˼��������ȡ�NaN ��ȼ��������������Τ��ȤǤ���̵������㳰�θ����Ȥʤ����Ǥϡ��ǥե���ȤȤ��� NaN ���֤���ޤ����������դϿ��ǤϤ���ޤ����������Ф��륪�ڥ��ɤΤ����줫�� NaN �ξ�硢��̤� NaN �ˤʤ�ޤ������������Ƥ� ɽ D-3 �˼������Τ����줫�˰��פ��ʤ��¤ꡢ̵�������㳰�ϵ����ޤ���20��
ɽ D-4 IEEE 754���㳰1 �����С��ե��� �� �ޤ��ϡ�xmax
round(x2-a) ��������ե��� 0�� �ޤ��� denormal
round(x2a) �����ˤ����� 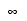
���ڥ��� ̵������� NaN���ڥ��� �����Τ���� round(x) round(x)
1 x ���������Τʷ�̡�ñ���٤� a =192�������٤� a =1536��xmax = 1.11 ...11 × �Ȥʤ�ޤ���
��= 10�� p = 3 �Υ����ƥ�ǡ�3.5
4.2 = 14.7 �����ΤǤ�����3.5
4.3 = 15.0 �����ΤǤϤʤ��Τ� (�������� 3.5��4.3 = 15.05)�������������㳰�������ޤ�����2 �ʿ����� 10 �ʿ��ؤ��Ѵ����Ǥϡ������������㳰����Ѥ������르�ꥺ��ˤĤ����������Ƥ��ޤ����ޤ�ɽ D-4 �ˡ�5 ������㳰��ư���ޤȤ�Ƥ���ޤ���
�����Τ������㳰�����ˤ˵�������ϡ�����������꤬�����ΤȻפ��ޤ�����ư�������ϡ��ɥ��������ȼ��Υե饰���Ѱդ���Ƥ��餺������˥��ڥ졼�ƥ������ƥ�˳��������ư�������㳰����𤹤�����ξ��ϡ������Τ������㳰���������Ȥ��Υ����ȤϤ����ƹ⤯�ʤ�ޤ�����������ϡ����եȥ��������ݻ����륹�ơ������ե饰����Ѥ���С���褷�ޤ����㳰�����Ƶ����������ǡ��������륯�饹�Υ��եȥ������ե饰�åȤ�����ư�������ϡ��ɥ������ˡ��б������㳰���饹��ޥ�������褦�˻ؼ����ޤ�������ʹߤ��㳰�Ϥ��٤ơ����ڥ졼�ƥ������ƥ�ؤβ�����ȼ�鷺�ˡ����������褦�ˤʤ�ޤ����桼���������ơ������ե饰��ꥻ�åȤ���ȡ��ϡ��ɥ������ޥ��������٥��͡��֥�ˤʤ�ޤ���
�ȥ�åץϥ�ɥ�
�ȥ�åץϥ�ɥ����Ѥ����̣�ϡ��ޤ����̤θߴ������ݻ����뤳�Ȥˤ���ޤ����㳰�������������ǥ��ܡ��ȤȤʤ��С������Υ����ɤǤϡ��ץ��������Ǥ��ڤ뤿��Υȥ�åץϥ�ɥ�ȡ��뤹�뤳�Ȥ��Ǥ��ޤ���
������äˡ�doSuntil(x�100)�Τ褦�ʥ롼�פ���Ѥ��륳���ɤ�ͭ���ˤʤ�ޤ���NaN �ϡ�<���塢>�� �� ��= (�� �Ϥʤ�) ����Ѥ���������Ӥ�����ɬ�������֤��Τǡ�x��NaN�ˤʤ�ȡ����Υ����ɤ�̵�¥롼�פ�����ޤ��������С��ե��������ǽ���Τ���
�Τ褦���Ѥ������Ȥ��˻��Ѥ����ȥ�åץϥ�ɥ����̤����ӤȤ������Ѥ��뤳�Ȥ�Ǥ��ޤ����п�����Ѥ��ơ�exp
���������ˡ�Ǥ������Υ��ץ�����������ϡ����٤˷礱�뤳�Ȥ˲ä��������С��ե����������ʤ����Ǥ�ñ���
�����⥳���Ȥ��礭���ʤ����ˤ���ޤ����ޤ�������������뤿��������С��ե���/��������ե�����������ƥ����Ȥ����ȥ�åץϥ�ɥ����Ѥ�����ˡ�⤢��ޤ� (Sterbenz��1974)��
���ιͤ����ϼ��ΤȤ���Ǥ����ޤ������˽������������ѥ���������ޤ���
������� k ���Ф��ƥ����С��ե��������ɬ�����ȥ�åץϥ�ɥ餬�������ͤ� 1 �������䤷���ؿ����åפ��ƥ����С��ե������ͤ��֤��ޤ���IEEE 754 ��ñ���٤Ǥϡ�emax = 127 �Ȥʤ�Τǡ�pk = 1.45 × 2130 �Ǥ���С������С��ե����������ȥ�åץϥ�ɥ餬�ƤӽФ���ޤ����ȥ�åץϥ�ɥ�ϻؿ����Ȥ��ϰϤ˥�åפ���pk �� 1.45 × 2-62 (��������) ���ѹ����ޤ���Ʊ�ͤˡ�pk ����������ե�������ȡ��������ͤ����ꡢ��λؿ������λؿ��˥�åפ���ޤ����軻�����٤ƽ���ä������ǥ����������ξ�硢�ǽ�Ū���Ѥ� pn �ˤʤ�ޤ������������Ǥ�����Ѥϥ����С��ե���������Ǥ���Х�������ե������ޤ�����ʬ�Ѥ���������ϰϤ�Ķ���Ƥ��ʤ����ϡ��ȥ�åץϥ�ɥ�ϸƤӽФ��줺�����ˤ��;ʬ�ʥ����Ȥ�ȯ�����뤳�ȤϤ���ޤ������С��ե����ޤ��ϥ�������ե��������������Ǥ⡢pk �Ϥ��줾�졢����Ū�����٤ξ軻����Ѥ��� Pk - 1 ���������Ƥ���Τǡ��п��Ƿ�����������Ϥ뤫�����ΤǤ���Barnett (1987) �ϡ������С��ե���/��������ե�����������Ȥ��������٤ˤ�äơ����Ф�ɽ�dz�����������ФǤ��������Ҳ𤷤ޤ�����
IEEE 754 �λ��ͤǤϡ������С��ե���/��������ե������ȥ�åץϥ�ɥ餬�ƤӽФ��줿�����ǡ����줬��åפη�̤�������Ȥ����Ϥ���ޤ��������С��ե������Ф����åפϡ���̤�̵�¤����٤Ƿ���������� 2a �ǽ��������塢�б��������٤˴ݤ�������������ޤ�����������ե����ξ��ϡ���̤� 2a �Ǿ軻���ޤ����ؿ��� ��ñ���٤ξ��� 192�������٤ξ��� 1536 �Ȥʤ�ޤ�������ϡ�1.45 × 2130 �� 1.45 × 2-62 ���Ѵ�����뤫��Ǥ���
�ݤ�⡼��
IEEE ɸ��Ǥϡ����줾����������Τ˷��������η�̤��ݤ���� (2 �ʿ����� 10 �ʿ��ؤ��Ѵ��Ͻ���) �Τǡ����ΤǤʤ���̤�����������ɬ�����ݤ�Ԥ��ޤ����ݤ�Ȥ����衢�Ǥ�ᤤ�ͤ�ɽ�魯�Ȥ������ȤǤ�������ʳ���ɸ��ˤϡ�0 �ؤδݤᡢ+
�ؤδݤᡢ-
�ؤδݤ�Ȥ��� 3 ����δݤ�⡼�ɤ�����ޤ���-
�ؤδݤ���������ؤ��Ѵ��ȤȤ�˻��Ѥ���ȡ��Ѵ��������ڤ겼���ؿ��Ȥ��ƹԤ��ޤ������� +
�˴ݤ��ȡ��ڤ�夲�ؿ��ˤʤ�ޤ���0 �ؤδݤᡢ�ޤ��� -
�ؤδݤͭ���ˤʤäƤ���Ȥ��ˡ������ͤ������С��ե�������ȡ��ǥե���Ȥη�̤� +
�ǤϤʤ���ɽ����ǽ�ʺ����ͤˤʤ�Τǡ��ݤ�⡼�ɤϥ����С��ե����˱ƶ���Ϳ���뤳�Ȥˤʤ�ޤ���Ʊ�ͤˡ�+
�ؤδݤᡢ�ޤ��� 0 �ؤδݤͭ���ˤʤäƤ���Ȥ�������ͤ������С��ե�������ȡ���κ����ͤ���������ޤ���
�ݤ�⡼�ɤ� 1 �Ĥα�����Ȥ��ơ����Х�η�������ޤ� (�⤦ 1 �Ĥα�����ϡ���2 �ʿ����� 10 �ʿ��ؤ��Ѵ����Ǽ����ޤ�)�����Х�η�����Ѥ����硢2 �Ĥ��� x��y ���¤Х�
�Ȥ��ư����ޤ���������
�� x
y ��-
�˸����äƴݤᡢ
�� x
y �� +
�˸����äƴݤ��Ȥ�����̣�Ǥ����û������Τʷ�̤ϡ����Х�
���ϰϤˤ���ޤ����ݤ�⡼�ɤ��ʤ���С����Х�η����̾
��
(������
�ϥޥ����ץ�����) �ˤ�äƼ¸����ޤ�21��
���η�̡����Х�Υ�������¿��˸��Ѥ���ޤ������Х���η�̤ϥ��Х�Ȥ��Ʒ������Τǡ��̾�����Ф������Ϥ⥤�Х�ǻ��ꤷ�ޤ���2 �ĤΥ��Х�
��
��û�����ȡ���̤�
(������
�ϴݤ�⡼�ɤ� -
�˥��åȤ���
���ޤ�
�ϴݤ�⡼�ɤ� +
�˥��åȤ���
) �ˤʤ�ޤ���
���Х������Ѥ�����ư�������黻��Ԥ��ȡ��ǽ�Ū�ʲ�ϡ����Τʷ���̤�ޤ।�Х�Ȥ��������ޤ�������ϡ����Х뤬���������� (�褯�����뤳�ȤǤ�)�����������Υ��Х����Ǥ�դ��ͤˤʤ�Τǡ�����ۤ������ǤϤ���ޤ����Х�η��ϡ�¿�����٤���ư�������ѥå�������ʻ�Ѥ���С�����˰�̣������ޤ����ޤ������������ p �ȤȤ�˷���Ԥ��ޤ������Х���η�̤ˤ�ꡢ�ǽ�Ū�ʲ������ΤǤ��뤳�Ȥ��狼��С��ǽ�Ū�ʥ��Х뤬Ŭ�ڤʥ������ˤʤ�ޤ��ʳ�Ū�����٤�夲�ʤ��顢���٤������ʤ����ޤ���
�ե饰
IEEEɸ��Ǥϡ������Ĥ��Υե饰�ȥ⡼�ɤ����ݡ��Ȥ���Ƥ��ޤ������Ǥ����������Ȥ��ꡢ5 ������㳰 (��������ե����������С��ե����������ˤ�������̵�����������Τ����) ���Ф��ƥ��ơ������ե饰���Ѱդ���Ƥ��ޤ����ޤ��ݤ�⡼�ɤˤϡ��Ǥ�ᤤ�ͤؤδݤᡢ+
�ؤδݤᡢ0 �ؤδݤᡢ-
�ؤδݤ�� 4 ���ब����ޤ������줾����㳰���Ф��ƥ��͡��֥롦�⡼�ɡ��ӥåȤ� 1 �ij��ݤ���褦�˶��������ᤷ�ޤ����ܹ�Ǥϡ��ƥ⡼�ɤȥե饰��ɤΤ褦��ͭ�������ѤǤ��뤫������Ĥ��Ҳ𤷤ޤ�������˹��٤���ˤĤ��Ƥϡ���2 �ʿ����� 10 �ʿ��ؤ��Ѵ����˼����Ƥ��ޤ���
xn (������ n ������) ������륵�֥롼��������ͤ��Ƥߤޤ���n > 0 �ξ��ϡ����Τ褦��ñ��ʥ롼�����ѤǤ��ޤ���
PositivePower(x,n) {while (n is even) {x = x*xn = n/2}u = xwhile (true) {n = n/2if (n==0) return ux = x*xif (n is odd) u = u*x}
������n < 0 �ξ��� xn ������뤵������Τ���ˡ�ϡ�
PositivePower(1/x,-n)�ǤϤʤ���1/PositivePower(x,-n)��ƤӽФ����ȤǤ���������ͳ�ϡ��ǽ�μ��ξ�硢�軻��Ԥ� n ���ͤ��Ȥˡ�1/x �ν���������줿�ݤ�������ޤޤ�뤳�Ȥˤʤ뤫��Ǥ���2 ���ܤμ��Ǥϡ����Τ��ͤη� (x) �ˤ�ȤŤ��ơ��Ǹ�˹Ԥ������Ǵݤ������ 1 �����ȼ���ޤ�����������������ˡ�ˤ����������ޤ���PositivePower(x,-n)����������ե����ˤʤ�ȡ���������ե������ȥ�åץϥ�ɥ餬�ƤӽФ���뤫�����뤤�ϥ�������ե��������ơ������ե饰�����åȤ���ޤ�������ư��ϡ�x-n ����������ե������������ǡ�xn �ϥ����С��ե����ˤʤ뤫���ϰ���˼��ޤ뤫�Τ����줫�ˤʤ�Τǡ�����Ǥ�22����������IEEE ɸ��Ǥϥ桼���������٤ƤΥե饰�˥��������Ǥ���Τǡ����֥롼����ˤ���ñ�ˤ���������뤳�Ȥ��Ǥ��ޤ���ñ�ˡ������С��ե���/��������ե��������͡��֥롦�ӥåȤդˤ��ơ������С��ե���/��������ե��������ơ������ӥåȤ���¸��������Τ��ȤǤ������θ塢1/PositivePower(x,-n)������ޤ��������С��ե�������������ե����Τ�����Υ��ơ������ӥåȤ⥻�åȤ���ʤ���С��ȥ�åס����͡��֥롦�ӥåȤȤȤ�˥��ơ������ӥåȤ��ꥹ�ȥ�����ޤ��������줫�Υ��ơ������ӥåȤ����åȤ��줿���ϡ��ե饰���ꥹ�ȥ����졢PositivePower(1/x,-n)����Ѥ��ƺƷ����ޤ������ξ��ϡ�Ŭ�ڤ��㳰�������ޤ����ե饰����Ѥ���⤦ 1 �ĤΥ������ϡ�arccos x = 2 arctan
�Ȥ��������� arccos�������Ȥ��˵����ޤ���arctan (
) ��ɾ���� ��/2 �Ȥʤ��硢arccos (-1) �ϡ�̵����α黻�˽��ä� 2��arctan (
) = �Ф�������ɾ������ޤ����������� (1 - x)/(1 + x) �η��ˤ�ꡢarccos (-1) ���㳰�ˤʤ�ʤ��Ƥ⡢�����ˤ������㳰�Υե饰�����åȤ���ޤ�����������ϴ�ñ�˲��Ǥ��ޤ����ޤ������ˤ������ե饰���ͤ���¸���Ƥ��顢arccos �������������λ�����塢��Ȥ��ͤ�ꥹ�ȥ����ޤ���
�����ƥ��¦��
����ԥ塼�������ƥ�Τ�����¦�̤��߷פ�����ˡ���ư�������˴ؤ����μ���ɬ�פˤʤ�ޤ�������ԥ塼���������ƥ�����ˤ��̾��ư������̿��Ȥ߹��ޤ�Ƥ���Τǡ�����ѥ���Ǥ�������ư������̿������������Ʊ���ˡ����ڥ졼�ƥ������ƥ�Ǥϡ�����ư������̿����Ф����㳰��郎ȯ���������ν��֤�Ƚ�Ǥ��ʤ���Фʤ�ޤ����̤ˡ����Ͳ��Ϥβ������ɤ�Ǥ⡢����Ū�����Ƥϥ��եȥ������Υ桼�����䳫ȯ�Ԥ��оݤ˽�Ƥ���Τǡ�����ԥ塼�������ƥ���߷ԤˤϤ���ۤɻ��ͤˤϤʤ�ޤ����߷�����ˤ����ɤ�����ͽ������������ȯŸ���뤫������Ȥ��ơ����� BASIC �ץ�������ͤ��Ƥߤޤ���
Borland �Ҥ� Turbo Basic �� IBM PC ��Ǽ¹Ԥ��ʤ��顢"
Not Equal" �Ƚ��Ϥ���ץ������Ǥ����������ʬ�Ϥϡ����ι�ǹԤ��ޤ����ʤ����嵭�Τ褦���ü�������ư����������Ʊ��˰������ȤϤǤ��ʤ��Ȥ�����Ŧ�⤢��Ȼפ��ޤ���������������������������ϰ� E ����˼��ޤ��ΤȤ�����̣�ǡ�Ʊ���Ǥ���Ȳ�ᤷ�Ƥ�������������ϡ�¿���������ˤʤ��Ʊ���ˡ�¿���ε�����褹��Τǡ���ǽŪ�ʲ����ˤϤʤ�ʤ��Τϸ����ޤǤ⤢��ޤ���E ���ͤϤɤΤ褦�ˤʤ�ΤǤ��礦��x < 0 �� y > 0 ���ͤ� E ���ϰ���ˤ����硢���줾��ۤʤ���椬����Τˡ��ºݤˤ��줬�����Ǥ���ȸ�����Ǥ��礦��������ˡ�a �� b ��|a - b| < E �Ȥ����롼�����������ط��ϡ�a �� b �� b �� c �� a �� c ���̣�����ΤǤϤʤ��Τǡ������δط��Ȥߤʤ����ȤϤǤ��ޤ���
̿��å�
���륢�르�ꥺ��ǡ����Τʷ�̤��������뤿��ˡ����٤ι⤤���硼�ȥС����Ȥ�ɬ�פˤʤ뤳�Ȥ�����ޤ���
����Ȥ��ơ����������κ��θ��� (
) /2a ���������ޤ���234�ڡ�������������Ȥ��ꡢb2
4ac�ΤȤ����ݤ�����ˤ�����������κ��θ����ǵ����η��Ⱦʬ������������ǽ��������ޤ���b2 - 4ac ����ʬ���������٤ǹԤ����Ȥˤ�ꡢ���������٥ӥåȤ�Ⱦʬ (���ʤ��ñ���٥ӥåȤ�����) ���ݻ�����ޤ���
a��b��c �γ��ͤ�ñ���٥ե����ޥåȤΤȤ��ˡ�2 �Ĥ�ñ���ٿ����ꡢ�����٤η�̤���������軻̿�����С�b2 - 4ac �������٤Ƿ�����Τϴ�ñ�Ǥ���2 �Ĥ� p ��������Τ˴ݤ��ˤϡ������οʹԤ˽��äƥӥåȤ��˴�������ǽ���Ϥ����ΤΡ��Ѥ� 2p �ӥå����Τ��������뤿��˾����ɬ�פˤʤ�ޤ����������äơ�ñ���٥��ڥ��ɤ��������٤��Ѥ������ϡ��ɥ��������̾ñ���٤ξ���ξ�����٥����Ȥ��⤯���ޤ������٤ξ�����⥳���Ȥ��㤯�ʤ�ޤ�������ˤ⤫����餺���Ƕ��̿��åȤϥ��ڥ��ɤ�Ʊ�����٤η�̤���������̿����������뷹��������ޤ�23��
2 �Ĥ�ñ���٥��ڥ��ɤ��Ȥ߹�碌�������٤η�̤���������̿������������κ��θ����˸¤ä�Ŭ�Ѥ�����硢̿��åȤ��ɲä��Ƥ��̣������ޤ�������������̿��ˤϤ��ޤ��ޤʻȤ���������ޤ������ΰ켡�������ηϤ���������ͤ��Ƥߤޤ���
a11x1 + a12x2 +������+ a1nxn= b1
a21x1 + a22x2 +������+ a2nxn= b2
� � �
an1x1 + an2x2 +������+ annxn= bn
����ϡ����Τ褦�� Ax = b �Ȥ��ƹ�������˽����뤳�Ȥ��Ǥ��ޤ���
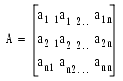
x(1) �β�����ξõ�ʤɤ���ˡ�Ƿ�����Ȳ��ꤷ�ޤ�����̤����٤��ȿ��Ū�����פ���ˡ�Ǿ夲�뤳�Ȥ��Ǥ��ޤ���
��= Ax(1) - b (12)
Ay = �� (13)
x(1) �����Τʷ��Ǥ����硢�Τ� y ��Ʊ�ͤ˥������٥����ˤʤ�ޤ������̤ˡ��Τ� y �η��ϴݤ�������䤹���Τǡ�Ay
x(2) = x(1) - y (14)��
Ax(1)-b = A (x(1)- x) �Ȥʤ�ޤ� (������ x �Ͽ��β� (̤��) �Ǥ�)��y
x(1)- x �Ȥʤ�Τǡ���γ����ϼ��Τ褦�ˤʤ�ޤ���
(12)�� (13)�� (14) �Υ��ƥåפ줾�� x(1) �� x(2) �ˡ��ޤ� x(2) �� x(3) ���֤������Ʒ����֤����Ȥ��Ǥ��ޤ���x(i+1) �� x(i) ������ΤǤ���Ȥ�����Ŧ�������ʤ�ΤǤϤ���ޤ��ܺ٤ˤĤ��Ƥϡ�Golub/Van Loan (1989) �Ȥ��Ƥ���������
ȿ��Ū������¹Ԥ���ȡ��Τϡ�����ͤǤϤ����Τ����Τˤϰ��פ��ʤ���ư���������κ��������������Ǥ�ޤ�٥����Ȥʤ�Τǡ��������껦�����꤬�ФƤ��ޤ����������äơ�ȿ��Ū�����ϡ���= Ax(1) - b �������٤Ƿ����ʤ��¤ꡢ����ۤɰ�̣������ޤ�����⡢�����������٤η�̤�ɬ�פȤ����Ȥ����ǡ�2 �Ĥ�ñ���ٿ� (A �� x(1)) ���Ѥ�����륱�������������ޤ���
����ȡ�2 �Ĥ���ư����������軻�������ڥ��ɤ� 2 �ܤ����٤��Ѥ��֤�̿��ϡ���ư������̿��åȤ��ɲä��뤳�Ȥ��Ǥ��ޤ������Τ��Ȥ�����ѥ����Ϳ����ƶ��ˤĤ��Ƽ����������ޤ���
����ȥ���ѥ���
����ѥ������ư����������ߴط��ˤĤ��Ƥϡ�Farnum (1988) �λ����˾ܤ�����������Ƥ��ޤ����ܹ������ʬ�ϡ����λ�������ȴ�褷����ΤǤ���
�����ޤ���
���������ˤ�äơ��ץ������˴ؤ���ʸ�����������褦�˸���ΰ�̣�����Τ˵���Ǥ���Τ�����Ū�Ǥ������Τ��Ȥϡ������������ʬ�ˤĤ��ƤϤ��ƤϤޤ��ΤΡ���ư�������˴ؤ���¤ꡢ�����������Τ������ޤ��Ǥ��뤳�Ȥ���¤Ǥ��������餯��������߷Ԥΰռ�����ˡ���ư�������ˤϴݤ�������դ���ΤǤ��뤿�ᡢ�����Ǥ����Τϲ���ʤ��Ȥ����פ����ߤ�����褦�˻פ��ޤ������ˤ��줬�����Ǥ���ʤ顢����ޤǤ������ϡ���������θ��ä�ǧ���ˤĤ��Ƽ¾ڤ��Ƥ������Ȥˤʤ�ޤ����ܹ�Ǥϡ���������˶��̤��Ƹ����뤢���ޤ����ˤĤ��ơ������н���ˡ�ʤɤ��濴���������ޤ���
�ä��٤����Ȥˡ�����ˤ�äƤ� x ����ư���������ѿ� (�㤨��
3.0/10.0) �Ǥ����硢10.0*x������뤿�Ӥˤ��٤�Ʊ���ͤˤʤ�Ȥ������Τʻ���Τʤ���Τ��褯����ޤ����㤨�С�Brown �Υ�ǥ�ˤ�ȤŤ� Ada �Ǥϡ���ư�������黻�� Brown �θ����������������Ƥ���н�ʬ�ʤΤǡ�����¿�����ͤ���äƤ��Ƥ⤫�ޤ�ʤ����Ȥˤʤ�ޤ�����ư���������ޤ��ʷ���ª����Ȥ������ϡ���ư�������α黻���Ȥ˷�̤����Τ��������ɬ�פΤ��� IEEE ��ǥ�ȤϤޤä����ۤʤ�Ȥ����Ǥ���
IEEE ��ǥ�Ǥϡ�(3.0/10.0)*10.0��3�ˤʤ뤳�Ȥ���� (���� 7) �Ǥ��ޤ�����Brown �Υ�ǥ�ǤϤ��������Ǥ��ޤ�������ʬ�θ�������˸�����⤦ 1 �ĤΤ����ޤ����ϡ������С��ե�������������ե���������¾���㳰���������Ȥ��ν�����ˡ�˴ؤ����ΤǤ���IEEE ɸ��Ǥϡ��㳰��ư����Τ˻��ꤵ���Τǡ�����ɸ����ǥ�Ȥ��ƻ��Ѥ�������Ǥϡ��������˴ؤ��뤢���ޤ�������������Ǥ��ޤ���
���ä��β��λ����⤢���ޤ��Ǥ�����ư���������ϴݤ������ȼ�����ᡢ����η��ˡ§��ɬ��������ư���������ˤ�Ŭ�ѤǤ��ޤ����㤨�С�x = 1030��y = -1030��
z = 1 �Ȥ�������(x+y)+z��x+(y+z)�β�Ϥޤä����ۤʤ�ޤ������Ԥξ��� 1 �ǡ���Ԥ� 0 �ˤʤ�ޤ������ä���Ĥ����Ȥν������Ϸ褷�ƶ�Ĵ�������뤳�ȤϤ���ޤ������� 3��4 ����� 6 �˼��������르�ꥺ��Ϥ��٤ơ����ä��ΰ��֤˰�¸���ޤ����㤨�С����� 6 �θ��� xh = mx - (mx - x) �ϡ��⤷���ä����ʤ���� xh = x �ˤʤꡢ���르�ꥺ�����Τ�̵��̣�ˤʤ�ޤ������ä��ΰ�̣��º�Ť���ɬ�פΤʤ����������ϡ���ư�������η��ˤϤۤȤ��̵��̣�Ǥ�����ʬ����ɾ�������Τ��������ʤ�������¿������ޤ�������
ds�������١�x��y��ñ���٤Ǥ���Ȳ��ꤷ�ޤ���ds+x*y�Ȥ������ǡ��Ѥ�ñ���٤������٤Τɤ���Ƿ������ΤǤ��礦���ޤ��̤���ǡ�x+m/n(������m��n�ϤȤ������ ) �μ�����������ư���������Τ�����Ƿ������ΤǤ��礦����������ˤ� 2 �Ĥ���ˡ���н�Ǥ��ޤ�����������ⴰ���ʲ����ˤϤʤ�ޤ���1 �Ĥϡ���������ѿ��٤�Ʊ�������פȤ��ư�����ˡ�Ǥ�������ϴ�ñ�ʲ����ˡ�Ǥ����������⤤���Ĥ�����ޤ����ޤ���Pascal �Τ褦�ʸ���Ǥϡ���ʬ�ϰϤΥ����פˤ�ä���ʬ�ϰ��ѿ����������ѿ���ʻ�ѤǤ���Τǡ�ñ�����ѿ����������ѿ��κ��Ѥ�ػߤ��Ƥ�ۤȤ�ɰ�̣������ޤ��ޤ�������˴ؤ�������⤢��ޤ���0.1*x�Ȥ������ξ�硢�ۤȤ�ɤθ���Ǥ� 0.1 ��ñ���٤�����Ȳ�ᤵ��ޤ��������Dz��ˡ��ץ�����ޤ���ư�������ѿ�������٤ơ�ñ���٤��������٤��ѹ����褦�ȹͤ����Ȥ��ޤ���0.1 �Τޤ�ñ��������Ȥ��ư����ȡ�����ѥ�����˥��顼�ˤʤ�ޤ������ξ�硢�ץ�����ޤ���ư����������٤�õ���ơ�������ѹ�����ɬ�פ�����ޤ���2 ���ܤΥ��ץ������ϡ����κ��Ѥ�ǧ��뤳�Ȥˤ�ꡢ��ʬ����ɾ���˴ؤ���롼���������ˡ�Ǥ�������ˤϻ��ͤˤʤ��㤬�����Ĥ�����ޤ���C �������������Ǥϡ���ư���������Ϥ��٤������٤Ƿ����ʤ���Фʤ�ޤ��� (Kernighan/Ritchie��1978)�����ξ��ϡ��ܹ�κǽ�˾Ҳ𤷤���Τ褦���к���⤿�餹�����Ȥʤ�ޤ���
3.0/7.0�������٤Ƿ�����ޤ�����q��ñ�����ѿ��ξ�硢����ñ���٤˴ݤ�Ƴ�Ǽ����ޤ���3/7 �� 2 �ʤν۴ľ����ˤʤ�Τǡ������٤ˤ����ͤϡ�ñ���٤dz�Ǽ���줿�ͤȤϰ��פ��ʤ��ʤ�ޤ����������äơ�q = 3/7�η��ϼ��Ԥ��ޤ�������ϡ����٤Ƥμ���Ǥ�⤤���٤Ƿ����Ƥ�ɬ���������Ū�ǤϤʤ����Ȥ���ΤǤ����⤦ 1 �Ĥ�������Ѥ˴ؤ����ΤǤ������Ѥ�¿���ιब�ޤޤ���硢�¤δݤ�������礭���ʤ��ǽ��������ޤ������δݤ��������������ˡ�Ȥ��ơ������٤��¤����Ѥ��뤳�Ȥ��Ǥ��ޤ� (������ˡ�ˤĤ��Ƥϡ��ֺ�Ŭ���ץ��������Ǿܤ����������Ƥ��ޤ�)��
d���������ѿ��ǡ�x[]��y[]��ñ��������ξ�硢���ѤΥ롼�פ�d=d+x[i]*y[i]�Τ褦�ˤʤ�ޤ���ñ���٤Ǿ軻��Ԥ��ȡ��������ѿ����ɲä���ľ�����Ѥ�ñ���٤��ڤ�ΤƤ���Τǡ������٤ˤ�����Ѥ������������ޤ������� 2 �Ĥ����Ŭ�Ѥ����롼��ϡ����뼰�Τ������ѿ���ǺǤ�⤤���٤Ƿ�����Ȥ�����ΤǤ�����������ȡ�
q=3.0/7.0���Τ�ñ���٤Ƿ�����24�����������ͤ�Ϳ���ޤ���������d=d+x[i]*y[i]�������٤Ƿ������Τǡ������٤����Ѥˤ������������Ū����������ޤ��������������Υ롼��Ϥ����륱�����ˤ��Τޤ�Ŭ�ѤǤ���櫓�ǤϤ���ޤ���dx��dy���������ѿ��ξ�硢y=x+single(dx-dy)�μ��ˤ������٤��ѿ����ޤޤ�ޤ��������ڥ��ɤ�ξ���Ȥ�ñ���٤Ǥ��뤳�Ȥ˲ä�����̤�ñ���٤ˤʤ�Τǡ������٤��¤���Ƥ��̣������ޤ��������ʣ������ʬ���˴ؤ���ɾ���롼��ϼ��ΤȤ���Ǥ����ޤ������줾��������Ф����������٤Ȥ����б����륪�ڥ��ɤκǤ�⤤���٤������Ƥޤ������γ�����Ƥϡ����Υĥ��¤���դ���ʬ���麬�������˹Ԥ��ޤ������ˡ��������դ��������ѥ������ꤷ�ޤ������Υѥ��Ǥϡ������˺ǹ�����٤ȡ��Ƥ����ᤵ������٤˳�����Ƥޤ���
q=3.0/7.0�ξ�硢�դ���ʬ��ñ���٤ˤʤ�Τǡ����Ϥ��٤�ñ���٤Ǽ¹Ԥ���ޤ���d=d+x[i]*y[i]�ξ��ϡ��軻�ΰ��Ū�����٤�ñ���٤ˤʤ�ޤ������ѥ��ǤϿƤ����������٥��ڥ��ɤ��ᤵ���Τ������٤˾��ʤ��ޤ���y=x+single(dx-dy)�Ǥϡ��û���ñ���٤Ǽ¹Ԥ���ޤ���Farnum (1988) �λ����Ǥϡ����Υ��르�ꥺ��Υ���ץ���Ȥ�����ۤ����ʤ����Ȥ��¾ڤ���Ƥ��ޤ������Υ롼��η����ϡ���ʬ����ɾ����������Ȥ߹��ޤ줿���˰�¸�������ˤ���ޤ�������ϡ�ʣ���ʥ������θ����ˤʤ뤳�Ȥ�����ޤ����㤨�С��ץ������ΥǥХå���Ȥ�ԤʤäƤ���Ȥ��ˡ���ʬ�����ͤ��ǧ��������礬����ޤ������ξ�硢�ץ�����������ʬ���ϡ����줬�Ȥ߹��ޤ줿���˰�¸����Τǡ�ñ�˥ǥХå�����ʬ�������Ϥ���ɾ������褦�˻ؼ����뤳�ȤϤǤ��ޤ��Ǹ�ˡ���ʬ���ˤϼ������꤬����ޤ���10 �ʿ�������� 2 �ʿ�����ؤ��Ѵ��� 1 �Ĥα黻�Ȥʤ�Τǡ�ɾ���롼��� 10 �ʿ�����β��˱ƶ���Ϳ����Ȥ������ȤǤ��������
0.1�Τ褦�� 2 �ʿ��Ǥ����Τ�ɽ���Ǥ��ʤ�����ξ����ä˽��פˤʤ�ޤ�������¾���Ȥ߹��ޤ�Ƥ���ư��� 1 �ĤȤ��Ƹ���˻ؿ����ޤޤ�Ƥ�����ˤ⡢�����ޤ���������ޤ�������Ū�ʻ�§�黻�ξ��Ȥϰۤʤꡢ�ؿ����ͤ�ɬ���������Τˤ�ɽ������ʤ���礬����ޤ� (Kahan/Coonen��1982)��
**���ؿ��ؿ��α黻�ҤǤ����硢(-3)**3���ͤ� -27 �Ȥʤ�ޤ���������(-3.0)**3.0�ʤɤξ�������ˤʤ�ޤ���**�黻�Ҥ������Τ٤��������å�����ȡ�(-3.0 )**3.0��
-3.03 = -27 �Ȥ��Ʒ����ޤ���������xy = eylogx �θ�������Ѥ��Ƽºݤΰ�����**���������ȡ�log �ؿ��ˤ�äƷ�̤�NaN(x < 0 �ΤȤ� log(x) =NaN�Ȥ�������ˤ�ȤŤ�) �ˤʤ뤳�Ȥ�����ޤ�������� FORTRAN ��CLOG�ؿ�����Ѥ���ȡ�ANSI FORTRAN ��ɸ��ˤ�ꡢCLOG(-3.0)�� i�� + log 3 (ANSI 1978) ����������Τǡ���� -27 �ˤʤ�ޤ���Ada ����Ǥϡ������Τ٤���˸¤äƻؿ���������뤳�Ȥˤ�ꡢ�����������Ƥ��ޤ���������ANSI FORTRAN �Ǥϡ������ºݤξ���Ǥ٤��褹�뤳�ȤϤǤ��ޤ���FORTRAN��ɸ��Ǥϡ����Τ褦�˵��ꤵ��ޤ���
- �ַ�̤����Ū������Ǥ��ʤ����ѱ黻�϶ػߤ�����
��������IEEE ɸ��ˡ�
�Ȥ�����ǰ��Ƴ�����줿���Ȥˤ�ꡢ������Ū������Ǥ��ʤ��פȤ���ɽ���Ϥޤä�����̣��ʤ��ʤ��ʤ�ޤ�����1 �Ĥ�����Ȥ��ơ���̵������˼�������ˡ��Ŭ�ѤǤ��ޤ������Ȥ��С�ab ���ͤ���ꤹ����ˡ�
x �� 0 �˽��äƤ��줾�� f(x) �� a��g(x) �� b �Ȥ������������������β��ϴؿ� f �� g �����ͤ��Ƥߤޤ���f(x)g(x) �ϤĤͤ�Ʊ���˸¤˶�Ť��Ȥ���С����줬 ab ���ͤȤʤ�ޤ�����������ˤ�ꡢ2· =����Ω���ޤ���1.0· �ξ�硢f(x) = 1��g(x) = 1/x �ΤȤ��ˡ��³��� 1 �˶�Ť��ޤ�����f(x) = 1 - x��g(x) = 1/x �ΤȤ��ϸ³��� e-1 �Ȥʤ�ޤ����������äơ�1.0· �� NaN �Ȥʤ�ޤ����ޤ� 0 0 �ξ��ϡ�f(x)g(x) = eg(x)log f(x) �Ȥʤ�ޤ���f �� g �ϲ��ϴؿ��ʤΤǡ�0��f(x) = a 1x1 + a 2x2 + ...�������
g(x) = b 1x1 + b 2x2 + ... �ΤȤ��� 0 ����ޤ����������äơ�
limx � 0g(x) log f(x) = limx � 0x log (x(a 1 + a 2x + ...) ) = limx � 0x log(a 1x) = 0 �ˤʤ�ޤ�������ˤ��٤Ƥ� f �� g ���Ф��ơ�f(x)g(x) �� e0 = 1 �Ȥʤ�ޤ������ʤ�� 0 0 = 1 �ˤʤ�ޤ� 25 26�������������Ѥ���ȡ����٤Ƥΰ������Ф���ؿ��ؿ�������������ޤ��ˤʤ�ޤ����ä�(-3.0)**3.0�� -27 ���������뤳�Ȥˤʤ�ޤ���IEEE ɸ��
�����IEEE ɸ����Ǥϡ�IEEE ɸ��μ����Ĺ�ˤĤ����������ޤ����������� IEEE ɸ��Ǥϡ���������Ĺ��ץ�����ߥ��줫�����ѤǤ��뤫�ˤĤ��Ƥϲ����ݾڤ���Ƥ��ޤ��������äơ�����ɸ��ݡ��Ȥ�����ư�������ϡ��ɥ������ȡ�C��Pascal��FORTRAN �ʤɤΥץ�����ߥ���δ֤����פ�������ΤϤ褯���뤳�ȤǤ���IEEE �ε�ǽ�ˤ�äƤϡ����֥롼���饤�֥��θƤӽФ��ˤ�äƥ��������Ǥ����Τ⤢��ޤ����㤨�С�IEEE ɸ��ˤϡ�ʿ���������Τ˴ݤ�ʤ���Фʤ�ʤ��Ȥ�����郎����ޤ���������б����ơ�ʿ�����ؿ����ϡ��ɥ��������ľ�ܥ���ץ���Ȥ���Ƥ��뤳�Ȥ��褯����ޤ������ε�ǽ�ˤϡ��饤�֥��ˤ���ʿ�����롼�������Ѥ��ƴ�ñ�˥����������뤳�Ȥ��Ǥ��ޤ�����������ɸ��������ˤ�äƤϡ����֥롼����Ǥϴ�ñ�˥���ץ���ȤǤ��ʤ���Τ⤢��ޤ����㤨�С�����ԥ塼������ǤϤۤȤ�ɤξ�硢��ư�������Υ����פ� 2 �������٤������ݡ��Ȥ���ޤ�������IEEE ɸ��Ǥϡ�4 ��������٤��Ѱդ���Ƥ��ޤ� (���Τ������侩�����Τ�ñ���٤˳�ĥ��ä�����ĥñ���٥ե����ޥåȡ�ñ���١������١���ĥ�����٥ե����ޥåȤǤ�)������ʳ��ˡ�̵����ΰ����Ȥ�������⤢��ޤ�����
��ɽ�魯����ϡ����֥롼���鶡��Ǥ��ޤ�����������������ѿ��Υ��˥���饤���Ȥ�����������ᤵ�������Ǥϡ�������������ѤǤ��ʤ��ʤ�ޤ���
�������̯�ʾ����Ȥ��ơ��ݤ�⡼�ɡ��ȥ�åס����͡��֥롦�ӥåȡ��ȥ�åץϥ�ɥ顢������㳰�ե饰�ǹ����������֤Ƿ���ȼ�����������ޤ���1 �ĤΥ��ץ������ϡ����֤��ɤ��ޤ��Ͻ��ߤ��뤿��Υ��֥롼������Ѱդ��뤳�ȤǤ�������ˡ��������ͤ�ưŪ�˥��åȤ�����Ȥ��ͤ��֤����� 1 ������ǽ����Ǥ���ƤӽФ��������ʾ�礬����ޤ����֥ե饰�������������Ȥ��ꡢIEEE �ξ��֤������뤿��ΰ���Ū�ʥѥ�����ϡ��֥��å����ޤ��ϥ��֥롼������ϰϤ˸¤äơ����ξ��֤��ѹ����뤳�ȤǤ�������ˤ�ꡢ�ץ������¦�ˤϡ��֥��å��νи�����졢õ���Ф���ô�ȡ����֤��������줿���Ȥ��ǧ�����Ȥ������뤳�Ȥˤʤ�ޤ������ξ�硢���֤�֥��å����ϰ��������������Ǥ����������������Ǥ���Modeula-3 �ϡ��ȥ�åץϥ�ɥ�ˤ��γ�ǰ��Ŭ�Ѥ�������Ǥ� (Nelson��1991)��
�������� IEEE ɸ���ץ���Ȥ���Ȥ��ˤϡ���θ���٤����������Ĥ�����ޤ��������� x �ˤĤ��� x - x = +0 �Ȥʤ�Τ�27��(+0) - (+0) = +0 �Ȥʤ�ޤ���
��������- (+0) = -0 �Ȥʤ�Τǡ�-x �� 0 - x �Ȥ���������뤳�ȤϤǤ��ޤ���NaN�ϡ��̤�NaN�ξ���ޤᡢƱ���ͤˤϷ褷�Ƥʤ�ʤ��Τǡ�x = x ��ɬ�����⿿�ˤϤʤ�ʤ��Ȥ�����ͳ���顢NaN��Ƴ�����뤳�ȤϺ���θ����ˤʤ�ޤ���IEEE ��Isnan�ؿ�����Ѥ��ʤ��褦�˿侩����Ƥ�����ϡ��ºݤˡ�x �� x �μ���NaN��ƥ��Ȥ���Ǥ��ñ����ˡ�Ǥ����ޤ�NaN�Ϥۤ��ο��Ȥν���˴�Ϣ�����ʤ��Τǡ�x �� y ���� x > y �Ȥ���������뤳�Ȥ�Ǥ��ޤ���NaN ��Ƴ������ȡ���ư������������ʬŪ�˽���դ�����Τǡ�<��=��>���ޤ��� unordered �Τ����줫���֤�compare�ؿ��ˤ�ꡢ�ץ�����ޤ���ӽ������ñ�˼¹ԤǤ���褦�ˤʤ�ޤ���IEEE ɸ��Ǥϡ������줫�Υ��ڥ��ɤ� NaN �ξ��ˡ�NaN ���֤�����Ū����ư����������������Ƥ���ޤ�����ʣ�����ξ��ˤϡ����������ɬ������ͭ���ˤʤ�Ȥϸ¤�ޤ�����դ�ץ��åȤ���Ȥ��˻��Ѥ�����Ψ������硢��Ϣ���ͤκ����ͤ�����뤳�Ȥ��Ǥ��ޤ������ξ�硢�����ͤ�����ñ�� NaN ��̵�뤹��С���̣������ޤ���
�Ǹ�ˡ��ݤ��������ˤʤ뤳�Ȥ�����ޤ���IEEE ɸ��Ǥϡ��ݤ�����̩���������Ƥ��ꡢ����ϴݤ�⡼�ɤθ��ߤ��ͤ˰�¸���ޤ����ݤ�⡼�ɤϡ����Ѵ��ˤ�������ۤδݤ�䡢�����������Ū��
round�ؿ��ȶ��礹�뤳�Ȥ�����ޤ������ʤ��IEEE �δݤ����Ѥ���ץ������Ǥϡ���������Υץ�ߥƥ��֤���ѤǤ���������������Υץ�ߥƥ��֤ϡ�����������ڤι����� IEEE �ޥ���ǥ���ץ���Ȥ���ˤ��Խ�ʬ�Ȥ������Ȥˤʤ�ޤ�����Ŭ���ץ������
����ѥ���˴ؤ�������ϡ���ư�������˴ؤ��������̵�뤹�뷹��������褦�Ǥ����㤨�С�Aho�� (1986) �ϡ�
x/2.0��x*0.5���֤������뤳�Ȥˤ�ꡢ�ɼԤ�x/10.0��0.1*x���֤��������ΤȲ�ᤷ�Ƥ��ޤ��ޤ����������������μ��ϡ�
0.1 �� 2 �ʿ������Τ�ɽ�����뤳�ȤϤǤ��ʤ��Τǡ�2 �ʿ��ޥ���Ǥ�Ʊ�����ޥ�ƥ������ˤϤʤ�ޤ����ܽ�Ǥϡ�x*y-x*z��x*(y-z)���֤������뤳�Ȥ��ᤷ�ޤ�������ϡ�yz �ΤȤ��ˡ����� 2 �Ĥμ����ޤä����ۤʤ��ͤ���äƤ�����Ǥ⤢�ƤϤޤ�ޤ�����Ŭ���ץ�����ब���������˰�ȿ���ƤϤʤ�ʤ��Ȥ������ϡ������ɤ��Ŭ������Ȥ��ϡ��ɤΤ褦�����ñ�̸��Ǥ���ѤǤ���Ȥ������Ҥ�Τ��������������ΤǤ���������ȿ�̡���ư�������Υ��ޥ�ƥ������Ϥ���ۤɽ��פǤϤʤ��Ȥ������ݤ�Ϳ���ޤ��������ɸ��Ǥ��ä��ΰ��֤�º�Ť��٤����˴ؤ�������̵ͭ����鷺�����Ǥ����������Ȥ���
(x+y)+z��x+(y+z)�βޤä����ۤʤ뤳�Ȥ�ͤ����ޤ����㤨�С����ä����ݻ��˿��������������ϡ����Υ����ɤ˸��뤳�Ȥ��Ǥ��ޤ���
���Υ����ɤϡ��ޥ����ץ�����˴ؤ��복��������ΤǤ�����Ŭ������ѥ��餬 eps + 1 > 1 �� eps > 0 �Ǥ��뤳�Ȥ�ǧ������ȡ��ץ������Ϥޤä����ۤʤ�ư������Ȥˤʤ�ޤ���1
x �� x (x
e
��-p) ��Ķ���뤳�Ȥ��ʤ��褦�ˡ��Ǿ��� x �����������ˡ�x/2 �� 0 (x
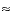
) �����˴ݤ��Ԥ������ x ������ޤ������μ�Ρֺ�Ŭ���פ��뤳�Ȥϡ���Ŭ���ˤ�äƼ����������ʥ��르�ꥺ����ݻ�����Ȥ�����̣�ǽ��פˤʤ�ޤ���
��ʬ����ʬ�������ο��Ͳ�Ȥ��ä���¿��������ϡ�¿���ι��ȼ���¤η���Ԥ���ΤǤ����û�����Ԥ����Ȥˡ�0.5 ulp ��θ��������������ǽ��������Τǡ������ι��ȼ���¤δݤ�����������礭���ʤ��礬����ޤ�������������褹���ñ����ˡ�ϡ���ʬŪ�ʲÿ����������ѿ��Ȥ��Ƴ�Ǽ�����Ʋû������줾�������٤Ǽ¹Ԥ��뤳�ȤǤ�������ñ���٤Ǽ¹Ԥ��ơ��¤������٤Ǽ¹Ԥ��뤳�Ȥϡ��ۤȤ�ɤΥ���ԥ塼�������ƥ�ǥ��ݡ��Ȥ���Ƥ��ޤ������������������Ǥ������٤ǹԤ��Ƥ�����ˡ����٤��ܲä���ΤϤ���ۤɴ�ñ�ǤϤ���ޤ��褯��Ƥ���� 1 �Ĥβ��ƤȤ��ơ��ƿ��ͤ��Ȥ��ơ���������˲û����Ƥ�����ˡ������ޤ������������¤����٤������˲����Ǥ��롢�Ϥ뤫�˸�ΨŪ����ˡ������ޤ������ʤ����������ˡ�Ǥ���
���� 8 (Kahan �β�ˡ����)
��ͭ�θ���
����Ѥ����¤������ȡ�
(������ |��j| < (n - j)e) �ˤʤ�ޤ������η�̤ϡ� Kahan �β�ˡ�����ξ�����٤����������������Ƥ��ޤ�������ñ��ʸ�������ǡ��Ʋÿ��ϡ�ne �����ư�αƶ��ϼ�������ñ�� 2e ����ư���������Ǥ����ܺ٤ˤĤ��Ƥϡ��ֲ�ˡ�θ������Ȥ��Ƥ���������
��ư�������黻�������ˡ§�˽��äƤ��뤳�Ȥ�����Ȥ����Ŭ���ץ������Ǥϡ���̤� C = [T-S] - Y = [(S+Y)-S] - Y = 0 �Ȥʤꡢ���르�ꥺ�ब�ޤä���̵��̣�ˤʤ�ޤ�����������ˤ�ꡢ�¿���Ŭ�Ѥ���������ñ�̸�����ư�������ѿ���ȼ�����˻��Ѥ�����ϡ���Ŭ���ץ������Ť˻��Ѥ���ɬ�פ�����Ȥ������Ȥ������ޤ���
����ˡ���Ŭ���ץ������ϡ���������ˤ���ư�����������ɤΥ��ޥ�ƥ��������Ѥ����ǽ��������ޤ���
1.0E-40*x�μ��Ǥϡ����ۤΤ����� 10 �ʿ����� 2 �ʿ�����ؤ��Ѵ����Ԥ��ޤ�����������ϡ�2 �ʿ������Τ�ɽ�����뤳�ȤϤǤ��ʤ��Τǡ������Τ������㳰�������ޤ����ޤ�������ñ���٤�ɾ�����줿���ϡ���������ե������ե饰�����åȤ���ޤ�������������ΤǤ����硢2 �ʿ��ؤ����Τ��Ѵ��ϡ�IEEE �ݤ�⡼�ɤθ��ߤ��ͤ˰�¸���ޤ����������äơ�����ѥ������1.0E-40�� 2 �ʿ����Ѵ������Ŭ���ץ������ˤ�ꡢ�ץ������Υ��ޥ�ƥ��������ѹ�����뤳�Ȥˤʤ�ޤ�����������27.5 �Τ褦������ϡ���������٤Ǥ����Τ�ɽ���Ǥ���Τǡ�����ѥ�������������Ѵ�����ޤ������ʤ�����Ĥͤ����Τ�ɽ�������Τǡ��㳰�ⵯ�������ݤ�⡼�ɤαƶ�������ʤ��Ȥ������ȤǤ�������ѥ�������Ѵ����٤�����ˤϡ��㤨��constpi=3.14159265�Τ褦������������Ѥ���ɬ�פ�����ޤ������̹�ξõ�ξ��⡢��Ŭ���ץ������ˤ�ä���ư�������Υ��ޥ�ƥ��������Ѥ������ǽ��������ޤ����㤨�С����Τ褦�ʥ����ɤǤ���
A*B�ϰ츫�����̹�Τ褦�˻פ��ޤ�����2 �����ɾ�����֤Ǥ��줾��ݤ�⡼�ɤ��ۤʤ�ΤǶ��̹�Ȥ��Ƥϰ����ޤ����� 3 �Ĥ��㤬�ͤ����ޤ����ޤ� x = x �ϡ��������true���֤������뤳�ȤϤǤ��ޤ�����ϡ�NaN ���̾����ư������������٤��羮��ɽ�魯���ȤϤǤ��ʤ��Τǡ�x �� NaN �ΤȤ�����Ω���ʤ���
x = +0 �ξ��� -x = 0 - x ����Ω���ʤ����ޤ� x < y �� x �� y �εդǤϤʤ����Ȥ�����ͳ�����뤫��Ǥ����ʾ���㤬����ȿ�̡���ư�����������ɤ��Ф��Ƹ��̤Τ����Ŭ���⤢��ޤ����ޤ�����ư����������ͭ���Ȥʤ������ñ�̸�������ޤ���IEEE �黻����Ȥ��� x + y = y + x�� 2 × x = x + x��1 × x = x�� 0.5 × x = x/2 �ʤɤ�����ޤ�����������������ñ���ñ�̸��ϡ�CDC �� Cray �Υ����ѡ�����ԥ塼����Ǥϼ��Ԥ��ޤ������Τۤ���̿��Υ������塼��䥤��饤�ץ����������ִ��⡢��Ŭ���ˤ�äƸ��̤���������Ȥʤ�ޤ�28��
3 ���ܤ���Ȥ��ơ�
dx=x*y(x��y�ϤȤ��ñ���٤��ѿ���dx�������٤�ɽ�路�ޤ�) �μ���ͤ��Ƥߤޤ���2 �Ĥ�ñ���ٿ���軻���������ٿ�����Ϥ���ޥ���Ǥϡ�dx=x*y�Ϥ��줾�쳺������̿��˥ޥåפ���ޤ����Ĥޤꥪ�ڥ��ɤ������٤��Ѵ����Ƥ��顢�����٤ξ軻��Ȥ�����Ϣ��̿��ؤΥ���ѥ���ϹԤ��ޤ�������ѥ�����߷Ԥ���ˡ�(x + y) + z ���� x + (y + z) �ؤ��Ѵ���ػߤ������¤ϡ��ܿ���ǽ�ʥȥ�å�����Ѥ���ץ�����ޤˤ�����Ϣ�Τʤ����ȤʤΤǡ�̵��̣�Ǥ���Ȥ�����Ŧ�⤢��ޤ��������餯���������ư�����������¿��Υ�ǥ�˽��äƤ���Τǡ��¿���Ʊ��ˡ§�˽����٤��Ǥ���Ȥ�������ˤ�ȤŤ���ΤǤ����¿��Υ��ޥ�ƥ�������ȼ������ϡ�����ץ���Ȥ���Τ˥����Ȥ�������Ȥ������Ǥ���2 �Ĥ� n �ӥåȿ���軻����ȡ��Ѥ� 2n �ӥåȤˤʤ�ޤ���
�ֳ֤ι����ؿ���ȼ�� 2 �Ĥ� n �ӥåȿ���û����뤴�Ȥˡ��¤Υӥåȿ��� n + �ؿ��֤δֳ֤�ɽ�蘆��ޤ����¤� (emax - emin) + n �ӥåȤȤʤꡢ���褽 2��emax + n �ӥåȤ��������ޤ���������α黻��Ԥ����르�ꥺ�� (�㤨�С���������β�ʤ�) �Ǥϡ�¿����ͭ�եӥåȤ�ޤ�����оݤȤ�������Ԥ��Τǡ���������������®�ˤʤ�ޤ����ޤ���sin �� cos �ʤɤ�Ķ�۴ؿ����ͤ�ͭ�����ˤϤʤ�ʤ��Τǡ������Υ饤�֥��ؿ���ץ���Ȥ���ΤϤ�������ʤ�ޤ���LISP �����ƥ�Ǥϡ����Τ������α黻������Ƥ��ơ�������褷�䤹����礬����ޤ��������������Τ���ư�������黻�ϤۤȤ�����Ω���ޤ���
�ºݤˤϡ�(x + y) + z �� x + (y + z) �Ȥ������¤����Ѥ��������ʥ��르�ꥺ�� (Kahan �β�ˡ�����ʤ�) ���Ѱդ���Ƥ��ꡢ�����ϰϤ�ͭ���Ǥ���¤ꡢ������ư��ޤ���
ab = (a + b)(1 +��)
�����ϰϤϡ����Τ���Ƥ�������ʬ�Υϡ��ɥ�������Ŭ�Ѥ����Τǡ����ͥץ�����ޤ������������르�ꥺ���̵�뤷���ꡢ����ѥ����߷Ԥ���ư�������ѿ��˼¿��Υ��ޥ�ƥ��������ݻ�����뤳�Ȥ�����Ȥ��ơ������Υ��르�ꥺ������Ѥ��ʤ����Ȥϡ������Ȥϸ����ޤ���
�㳰����
�����ޤǤ������ϼ�ˡ������ƥब�������٤ΰ�̣�˴ؤ����ΤǤ������ȥ�åץϥ�ɥ�⡢�����ƥ�˴ؤ��붽̣��������������ΤǤ���IEEE ɸ��Ǥϡ��桼������ 5 �ĤΥ��饹�γ��㳰���Ф���ȥ�åץϥ�ɥ�����Ǥ���褦�ʻ��ͤ������侩����Ƥ��ޤ����֥ȥ�åץϥ�ɥ���Ǥϡ��桼����������Ǥ���ȥ�åץϥ�ɥ�Υ��ץꥱ���������Ĥ��Ҳ𤷤ޤ�����̵�������䥼���ˤ��������Ԥ�줿��硢�ϥ�ɥ�ˤϳ������륪�ڥ��ɡ����뤤�����Τ˴ݤ��̤�����ɬ�פ�����ޤ������Ѥ���ץ�����ߥ���ˤ�äƥȥ�åץϥ�ɥ�ϡ��ץ��������Τ���¾���ѿ��ˤ⥢�������Ǥ����礬����ޤ������٤Ƥ��㳰�ˤĤ��ơ��ȥ�åץϥ�ɥ�ϡ��¹Ԥ��줿�������ơ�����Ӱտޤ��줿���٤��̤Ǥ��ʤ���Фʤ�ޤ���
IEEE ɸ��Ǥϡ�������ǰŪ�˥��ꥢ������ǹ������졢���餫���㳰���������������������Ƥȥ��ڥ��ɤ��̤Ǥ��뤳�Ȥ�����Ȥ��Ƥ��ޤ����ѥ��ץ饤��ǽ��¿�ű黻��˥åȤݡ��Ȥ����ޥ���Ǥϡ��㳰�����������ˡ�ñ�˥ȥ�åץϥ�ɥ�ǥץ�����५��������å�����������Ǥ��Խ�ʬ�ˤʤ���⤢��ޤ������ʤ���������Ƥ����Τ˼��̤Ǥ���ϡ��ɥ�������ɬ�פˤʤ�Ȥ������ȤǤ���
���Υץ��������ʬ�ϡ��ޤ��̤����������ΤǤ���
2 ���ܤξ軻�ˤ���㳰�������ơ��ȥ�åץϥ�ɥ餬
a���ͤ���Ѥ�������ΤȲ��ꤷ�ޤ����û��Ⱦ軻������Ū�˼¹ԤǤ���ϡ��ɥ������Ǥϡ���Ŭ���ץ������ˤ�äơ�2 ���ܤξ軻��Ϥ�����˲û�����ư�����Τǡ����βû������Ϻǽ�ξ軻���¹Ԥ��Ƽ¹Ԥ��뤳�Ȥ��Ǥ��ޤ����������äơ�2 ���ܤξ軻���ȥ�åפ���Ƥ⡢a=b+c�μ¹Ԥ�����äƤ���Τǡ�a�η�̤������ѹ�����Ƥ����ǽ��������ޤ�����������ư�������黻���ȥ�åפ�����ǽ�������ꡢ���η�̡���Ŭ�������塼�뤹��̿����٤ƾõ��뤳�Ȥ����뤿�ᡢ����ѥ���ǡ��ʾ�Τ褦�ʺ�Ŭ�����뤳�ȤϤ褤��ˡ�Ȥϸ����ޤ���������ϡ��ȥ�åץϥ�ɥ餬�ץ����������ѿ���ľ�ܥ�����������Τ٤ƶػߤ��뤳�Ȥˤ�äƲ��Ǥ��ޤ�������ˡ��ϥ�ɥ�ˤϰ����Ȥ��ơ����ڥ��ɤޤ��Ϸ�̤��Ϥ����Ȥ��Ǥ��ޤ�������Ǥ�ʤ����̤����꤬�Ĥ�ޤ������Υ�������ʬ�ξ�硢2 �Ĥ�̿�����Ū�˼¹Ԥ�����ǽ��������ޤ���
�軻���ȥ�åפ����ȡ����ΰ���
z�����Ǥ˼��βû��ˤ�äƾ����Ƥ����ǽ��������ޤ����äˡ��û��Ͼ軻�����®�ǽ��������Τǡ����줬���ƤϤޤ�ޤ���IEEE ɸ��ݡ��Ȥ��륳��ԥ塼�������ƥ�Ǥϡ�z���ͤ�ϡ��ɥ���������¸���뤫�����뤤�Ϻǽ�λ����ǥ���ѥ���ˤ��Τ褦�ʾ���������뤫���Ȥ��ä����餫�μ��ʤ�ɬ�פˤʤ�ޤ���Kahan�ϡ��ȥ�åץϥ�ɥ������ˡ������ִ��פȤ�����ˡ�ˤ�äƤ���������������Ǥ������Ƥ��Ƥ��ޤ���������ˡ�Ǥϡ������㳰�������������ǡ����η�̤Ȥ��ƻ��Ѥ����ͤ��㳰�����Ƥ�桼�������Ȥ����ꤷ�ޤ����㤨�С�(sin x)/x ������륳���ɤǡ��桼������ x = 0 �Ȥʤ뤳�ȤϤۤȤ�ɤʤ���Ƚ�Ǥ�����ǡ�x = 0 �Υƥ��Ȥ��ά��������� 0/0 �ȥ�åפ������������ǡ����Υ��������б������뤳�Ȥˤ�äƥѥե����ޥ�����������Ȥ��ޤ���IEEE �ȥ�åץϥ�ɥ����Ѥ����硢�桼�����ϡ�sin x/x �η���Ϥ�����ˡ��ޤ��� 1 ���֤��ϥ�ɥ�������������ȡ��뤷�ʤ���Фʤ�ޤ����������ִ������Ѥ���С�̵�����������������ǡ��� 1 ����Ѥ���褦�˻��ꤹ������ǺѤߤޤ� (�㳰���ºݤ˵��������ˡ����Ѥ����ͤ���ꤷ�Ƥ���ɬ�פ����뤫��Ǥ�)���ȥ�åץϥ�ɥ�ξ�硢�֤�����ͤϥȥ�åפ������������Ƿ����뤳�Ȥ��Ǥ��ޤ���
���ִ��������ϡ��ϡ��ɥ������μ������狼��䤹���ʤ�Ȥ������Ǥ�29���㳰�Υ����פ����ꤵ�줿�����ǡ�������Ȥˡ�ɬ�פ����η�̤���¸�����ơ��֥�Ȥ����뤳�Ȥ��Ǥ��ޤ������ִ��ˤϤ����Ĥ������������������IEEE ��ɸ�ब���Ǥ˹�����ڤ��Ƥ��뤳�Ȥ����ϡ��ɥ�����������ˤ�����������ˤ�Ǥ���Ȥ������꤬����ޤ���
�ܺ�
�����ޤǡ���ư�������黻�˴ؤ����������ˤĤ��ơ����ޤ��ޤʴ������鸡Ƥ���Ƥ��ޤ��������θ�ι�Ǥϡ���ư���������褷������ǤϤʤ�������ޤǤ˻�Ŧ����Ƥ�������Ϥ��٤ƿ���Ū�˸��ڤǤ���狼��䤹������Ǥ���Ȥ�������¾ڤ��Ƥ����ޤ������ι���礭�� 3 �Ĥ�ʬ���뤳�Ȥ��Ǥ��ޤ����� 1 ���Ǥϡ�������ʬ�Ϥ˴ؤ���Ƴ��������Ԥ��ޤ����ޤ� 177�ڡ����˼��������ݤ�����פˤĤ��ƾܤ����������ޤ����� 2 ���Ǥϡ�2 �ʿ����� 10 �ʿ��ؤ��Ѵ��ˤĤ��ơ���IEEE ɸ����˴ؤ�����������Ԥ��ޤ����� 3 ���Ǥϡ��֥����ƥ��¦�̡����㼨������Kahan�β�ˡ�����פˤĤ��ƾܤ����������ޤ���
�ݤ����
�ִݤ�����פι�Ǥϡ��ݸ��� 1 ����ݤ���С��û��ȸ�����ɬ�����Τ˼¹Ԥ������������ޤ��� (���� 2)�������Ǥϡ����θ��ڤ�Ԥ��ޤ������� 2 �ϡ��û��˴ؤ����Τȡ������˴ؤ����Τ� 2 �Ĥ���ʬ�ǹ�������ޤ��������˴ؤ��������ϼ��ΤȤ���Ǥ���
���� 9
- x �� y �����ѥ����� �� p ��ȼ���ե����ޥåȤ�������ư����������ɽ�魯��硢p + 1 �� (1 ����ݸ��) �Ǹ�����Ԥ��ȡ���̤����дݤ������
e �� 2e �ʲ��ˤʤ롣
����
y -
- x > y �ˤʤ�褦�ˡ�ɬ�פ˱����� x �� y �����촹���ޤ���x �� x0.x1 ... xp-1 × b0 �ˤʤ�褦�� x �� y ���ಽ (��������) ���Ƥ⤫�ޤ��ޤ���y �� y0.y 1 ...yp-1'��ɽ�蘆����硢���κ������ΤǤ����ޤ� y �� 0.y 1 ... yp �ξ�硢�ݸ��ˤ�äƷ��ͤκ��ϡ��ݤ���������� e����ˤʤ�褦�ˡ���ư���������˴ݤ���Τʺ���ɽ�魯���Ȥˤʤ�ޤ���
���̤ˡ�y = 0.0 ... 0yk+1 ... yk+p��������ϡ�p + 1 ����ڤ�ΤƤ� y �Ȥʤ�ޤ���
����ˤ�ꡢ���μ�������Ω���ޤ���< (�� - 1)(��-p - 1 + ��-p - 2 +...+ ��-p - k) (15)
|��| �� (��/2)��-p (16)
- �ݸ���������顢x - y �η��ͤ� x -
����ư���������˴ݤ�͡����ʤ�� (x -
) + ��(�ݤ���� �� �ϼ��μ����������ޤ�) �ˤʤ�ޤ���
- ���Τʺ��ϡ�x - y �ʤΤǡ������� (x - y) - (x -
+ ��) =
- y +�Ĥˤʤ�ޤ������ξ�硢���� 3 �ĤΥ��������ͤ����ޤ���x - y �� 1 �ξ�硢���и����ϼ����ϰϤˤʤ�ޤ���
���-p [(��- 1)(��-1 +...+��-k)+��/2] <��-p(1+��/2) (17)
- x -
< 1 �ξ��ϡ���= 0 �ˤʤ�ޤ���x - y ������Ǿ��ͤϼ��ΤȤ���Ǥ���
> (��- 1)(��-1 +...+ ��-k), (��������= �� - 1)
- �������äơ����ξ������и����ϼ����ϰϤˤʤ�ޤ���
(18)
- �Ǹ�ϡ�x - y < 1 �ΤȤ��� x -
�� 1 �Ȥʤ륱�����Ǥ�������ϡ�x -
= 1 �ξ�� (���ʤ����= 0) �˸¤äƵ����ޤ�����= 0 �ξ��ϡ����� (18) ��Ŭ�Ѥ����Τǡ����и������ϰϤ� ��-p < ��-p (1 + ��/2) �Ȥʤ�ޤ�����
��= 2 �ξ�硢�ϰϤ����Τ� 2e�Ȥʤꡢ�����ϰϤ� p ��
�Ȥ��� x = 1 + 22-p ��
y = 21-p - 21-2p ���Ф��������ޤ���Ʊ�����ο���û�������ϡ�������˸���褦�ˡ��ݸ�夬�ʤ��Ƥ⡢���Τʷ�̤������ޤ������� 10
- x �� 0��y �� 0 �ξ�硢x + y �������Ȥ������и����ϡ��ݸ�夬�ʤ����Ǥ⡢���� 2�����ޤ����롣
����
- k ���ݸ����Ф��륢�르�ꥺ��ϡ������Υ��르�ꥺ��˻��Ƥ��ޤ���x �� y �ξ��ϡ�x �� y �δ���ΰ��֤��礦�ޤǡ�y �˥��եȤ��ޤ���p + k �ΰ��֤�Ķ�������̵�뤵��ޤ������� p + k ��� 2 �Ĥο����¤���ޤ������� p ��˴ݤ�ޤ���
- �ݸ�����Ѥ��ʤ����������ˤĤ��Ƹ��ڤ��ޤ� (����Ū�ʥ�������Ʊ���Ǥ�)��x �� y �� 0������� x �� d.dd... × ��0 �η����˴�ಽ (��������) ���뤳�Ȥ�����Ȥ����������������뤳�ȤϤ���ޤ��ޤ������������ȤϤʤ���ΤȤ��ޤ���y �ν���꤫�饷�եȥ��դ�������ͤ� ��-p+1 ��꾯�ʤ����¤� 1 �ʾ�Ȥʤ�Τǡ����и����� ��-p+1 /1 = 2e �Ȥʤ�ޤ���
- ���������������Ȥ�ȼ����硢���եȤˤ�������
��-p+2 �δݤ�������ɲä���ɬ�פ�����ޤ���
- �¤� b �ʾ�ˤʤ�Τǡ��ݤ������
�� 2��
- �ʲ����ޤ����ޤ�����
����� 2 �Ĥ��������Ȥ߹�碌�뤳�Ȥˤ�ꡢ���� 2 ��Ƴ�����Ȥ��Ǥ��ޤ������� 2 �ϡ�1 �������¹Ԥ������ȼ�����и���������ΤǤ���x2 -y2 �� (x + y) (x - y) �δݤ��������Ӥ����硢¿������ȼ�����и������θ���ʤ���Фʤ�ޤ���x
xy �����и����ϡ���1= [(x
y) - (x - y)]/(x - y) �Ȥʤꡢ|��1|�� 2e �ξ����������ޤ����ޤ������Τ褦�˽��Ȥ�Ǥ��ޤ���
y = (x - y) (1 + ��1), |��1| �� 2e (19)
xy = (x + y) (1 + ��2), |��2|�� 2e (20)
�ޤ����Τ��Ѥη��ȴݤ�ˤ�äƾ軻��Ԥ��Ȥ���ȡ����и����Ϻ��� 0.5 ulp �Ȥʤ�Τǡ���ư�������� u �� v �ˤϼ��μ�������Ω���ޤ���
uv = uv (1 + ��3), |��3| �� e (21)
��� 3 �Ĥ����������Ȥ߹�碌�� (u = x
(xy������� v = x
y) �ȡ����Τ褦�ˤʤ�ޤ���
y)
(x
y) = (x - y) (1+��1) (x + y) (1 +��2) (1 +��3) (22)
�������äơ� (x - y) (x + y) �������Ȥ��˵��������и����ϼ��Τ褦�ˤʤ�ޤ���
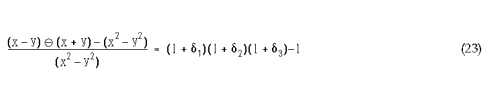
���и����ϡ���1+��2+��3+��1��2+��1��3+�� 2�� 3+�� 1�� 2�� 3 �ˤʤꡢ�ϰϤ� 5��+ 8��2 �Ȥʤ�ޤ������ʤ���������и����� 5 (�ݤ����) �Ȥʤ�ޤ� (e ���Ǿ����ǡ�e2 �Ϥۤ�̵��Ǥ��ޤ�)��
(x
(xx)
(y
y) ��Ʊ���褦��ʬ�Ϥ��Ƥ����и����Ͼ������ͤˤϤʤ�ޤ�����ϡ�x �� y �Ȥ��� 2 �Ĥζᤤ�ͤ� x2 - y2 �����������ȡ����и������̾�����礭���ʤ뤿��Ǥ������ξ�硢 (x
y)
(x
y) �ǿ��ˤʤä�ʬ�Ϥ�Ƥӻ��Ѥ��ơ����μ������뤳�Ȥ��Ǥ��ޤ���
x)
(y
y) = [x2(1 + ��1) - y2(1 + ��2)] (1 + ��3)
= ((x2 - y2) (1 + ��1) + (��1 - ��2)y2) (1 + ��3)
x �� y ���ͤ��ᤤ��硢�����ι� (��1-��2) y2�ϡ����� x2 - y2 ��Ʊ�����餤�礭���ʤ뤳�Ȥ�����ޤ����ʾ�η��ˤ�äơ�x2 - y2 ��� (x - y) (x + y) �Τۤ���������ΤǤ���Ȥ������Ȥ��¾ڤ��줿���Ȥˤʤ�ޤ���
���ˡ����ѷ������Ѥ˴ؤ��������ʬ�Ϥ��ޤ������� (7) �������Ȥ��˵��������������Ѥ��ˤϡ����λ��¤�ɬ�פˤʤ�ޤ���
���� 11
- �ݸ��Ǹ�����Ԥ��ȡ�y/2 �� x �� 2y �ξ��ˡ�x - y �����Τ˷�����롣
����
- x �� y ��Ʊ���ؿ��������硢x
y �����Τ˷�����ޤ�������ʳ��ξ�硢�����ξ�狼�顢�ؿ��κ��Ϻ��� 1 �Ǥ���ȸ����ޤ���0 �� y �� x �ˤʤ�褦�ˡ�ɬ�פ˱����� x �� y �����촹���ơ�x �� x0.x1 ...xp - 1������� y �� 0.y 1 ... yp �Ȥʤ�褦�� x �� y ���ಽ (��������) ���Ƥ⤫�ޤ��ޤ���x
y ������륢�르�ꥺ��ϡ��ޤ� x - y �����Τ˷����ơ�������ư�������˴ݤ���ΤǤ������� 0.d 1 ... dp �η����ξ�硢���κ���Ĺ���Ϥ��Ǥ� p ��ˤʤäƤ���Τǡ��ݤ�����ɬ�פ���ޤ���x �� 2y �Ȥʤ�Τǡ�x - y �� y���ޤ� y �� 0.d1 ... dp �Ȥʤ�Τǡ�x - y �ˤʤ�ޤ�����
�� > 2 �ξ�硢���� 11 �� y/�¡� x �� ��y ���֤������뤳�ȤϤǤ��ޤ���y/2�� x �� 2y �ζ�����郎ɬ�פˤʤ�ޤ������� 10 �ξ�����ľ��˼����� (x - y) (x + y) �θ���ʬ�Ϥϡ��û��ȸ����δ��ܱ黻��˵��������и����Ͼ����� (���� (19)��(20)) �Ȥ������¤�����ˤ�����ΤǤ�������ϡ��Ǥ����Ū�ʸ���ʬ�Ϥ���Ǥ������� (7) ��ʬ�Ϥ���ˤϡ����ξ����Ǽ����Ȥ��ꡢ���� 11 �Τ褦�ʾ�郎ɬ�פˤʤ�ޤ���
���� 12
- �ݸ��Ǹ�����Ԥ���硢a��b��c �����ѷ��� 3 �� (a �� b �� c) �Ȥ���ȡ�
(a +(b + c))(c -(a - b))(c +(a - b))(a +(b - c)) �������Ȥ������и����Ϻ��� 16��(������ e < 0.005) �ˤʤ롣����
(a + b + c) (1 - 2��)2 �� [a + (b + c) (1 - 2��)] � (1-2��)
- �ƹ�� 1 �Ĥ��ĸ��ڤ��Ƥߤޤ������� 10 ��ꡢb
c = (b + c ) (1 +��1) (��������1 �����и�����|��1| �� 2��) ��Ƴ�����Ȥ��Ǥ��ޤ����ǽ�ι���ͤ�
(a(b
c)) = (a +(b
c)) (1 +��2) = (a +(b + c) (1 +��1)) (1 +��2) �ˤʤꡢ���Τ褦�ˤʤ�ޤ���
�� a(b
c)
�� [a + (b + c) (1 + 2��)] (1 + 2��)
�� (a + b + c) (1 + 2��)2
(a
- ���ʤ������1 �� 1 �ĤʤΤǡ����θ���������Ω���ޤ���
(b
c)) = (a + b + c) (1 + ��1)2, |��1| �� 2�� (24)
(c
- ���ι�ˤϡ�a
b �˴ݤ������ޤळ�Ȥ�����Τǡ�c �� a
b �˰����θ�����ȼ����ǽ��������ޤ���a��b��c �ϻ��ѷ��� 3 �� (a �� b + c ) ��ʤ������μ���
c �� b �� a �ν�����Ȥ߹�碌��ȡ�a �� b + c �� 2b �� 2a �Ȥʤ�ޤ����������äơ�
a - b ������ 11 �ξ����������ޤ������ʤ�� a - b = ab �����������Ȥˤʤꡢc
(a - b) �Ȥ���������̵���ʤΤǡ����� 9 ���鼡�Τ褦��Ƴ�����Ȥ��Ǥ��ޤ���
(a
b)) = (c - (a - b)) (1 +��2), |��2| �� 2�� (25)
(c
- 3 ���ܤι�ϡ�2 �Ĥ����Τ��������¤�������ΤʤΤǡ����Τ褦�ˤʤ�ޤ���
(a
b)) = (c + (a - b)) (1 + ��3), |��3| �� 2�� (26)
(a
- �Ǹ�ι�ϡ����� 9 �� 10 �ˤ�ȤŤ��Ƽ��Τ褦�ˤʤ�ޤ���
(b
c)) = (a + (b - c)) (1 + ��4)2, |��4| �� 2�� (27)
(a
- x
y = xy (1+��) (������|�� | ���) �Ȥʤ�褦�ˡ��軻�����Τ˴ݤ��ȡ����� (24)�� (25)�� (26)�� (27) ���Ȥ߹�碌�ϼ��Τ褦�ˤʤ�ޤ���
(b
c)) (c
(a
b)) (c
(a
b)) (a
(b
c))
��(a + (b + c)) (c - (a - b)) (c + (a - b)) (a + (b - c)) E
E = (1 + ��1)2 (1 +��2) (1 + ��3) (1 +��4)2 (1 + ��1)(1 + ��2) (1 + ��3)
- ��������
- E �ξ�¤ϡ� (1 + 2��)6(1 +��)3 �Ȥʤꡢ�ϰϤ� 1 + 15��+ O (��2) �Ȥʤ�ޤ��������Ԥˤ�äƤ� O (e2) ��ñ��̵�뤹����⤢��ޤ���������ϴ�ñ�������Ǥ��ޤ���
(1 + 2��)6(1 +��) 3 = 1 + 15��+��R(��)�ȵ��Ҥ���ȡ�R(��) �����η�������� e ��¿�༰�Ȥʤ�Τǡ��Ť������ؿ��ˤʤ�ޤ���R (0.005 ) = 0.505 �ʤΤǡ���< 0.005 �ˤϤ��٤� R(��)< 1 �ȤʤꡢE �� (1 + 2��)6(1+��)3 < 1 + 16�Ť�����Ω���ޤ���
E �β��¤�����硢1 - 15�� - ��R(�� ) < E �Ȥʤ�Τǡ���< 0.005 �ΤȤ���
1 - 16��< (1 - 2��)6(1 - ��)3 �ˤʤ�ޤ�������� 2 �Ĥ��ϰϤ��Ȥ߹�碌��ȡ�
1 - 16��< E < 1 + 16�Ťˤʤ�ޤ����������äơ����и����Ϻ��� 16�ŤǤ��������� 12 �ϡ����� (7) �˰������껦�ϵ����ʤ����Ȥ���������ΤǤ��������Ǹ��� (7) ������Ū�˰��ꤷ�Ƥ��뤳�Ȥ��������ޤǤ⤢��ޤ����������Τ�ͭ���ϰ� (���껦���˼������� 3 �Ƿ�ޤ��ϰ�) ���ꤷ�Ƥ����Τ��褤��ˡ�Ǥ���
���� 3 ���
- ���Τ褦�˲��ꤷ�ޤ���
- q = (a + (b + c)) (c - (a - b)) (c + (a - b)) (a + (b - c))
- �����
- Q = (a
(b
c))
(c
(a
b))
(c
(a
b))
(a
(b
c))
- ���� 12 �ˤ�ꡢQ = q (1 +��) (�������ġ�16��) ������Ω���ޤ���
�ġ�0.04/ (0.52) 20.15�Ȳ��ꤹ��С����μ��ϡ���ñ�˥����å��Ǥ��ޤ���
(28)
- �ޤ���|��| �� 16�� �� 16 (0.005 ) = 0.08 �Ȥʤ�Τǡ��Ĥ��������������Ȥˤʤ�ޤ����������äơ�|��1| �� 0.52|��| �� 8.5�Ťξ�硢
�Ȥʤ�ޤ���
- ������ 0.5
ulp����Ȥ���ʿ�����������ȡ��������Ȥ��θ����ϡ�|��2| ��Ťξ��ˡ�(1 +��1) (1 +��2) �ˤʤ�ޤ�����= 2 �ξ�硢4 �ǽ��������Ǥ⤳��ʳ��θ�����Ƴ������ޤ�����¾�ξ�硢�����ˤϤ⤦ 1 �Ĥΰ���
1 +��3 (|��3| ���)��ɬ�פǡ��ޤ������� 12 �ξ����˼�������ˡ�ˤ�äơ�
(1 +��1) (1 +��2) (1 +��3) �κǽ�Ū�ʸ������ϰϤ� 1 +��4 �˰�¸���ޤ�
(������ |��4| �� 11��)�������� 4 ��ľ��˼�������ǼŪ������������Τ�ɽ���Ǥ���褦�ˡ����������� ��(x) ���ɤ�ۤ�������᤹ܶ�뤫������ΤǤ���
���� 13
- ��(x) = ln (1+ x)/x �Ȥ���ȡ�0 �� x ��
�ξ�硢
�� ��(x) �� 1 �ˤʤꡢ������ʬ��
|��'(x)| �������������Ȥˤʤ롣
����
- ��(x) = 1 - x/2 + x2/3 - ...�ϲ��߹�θ������ʤΤǡ�x �� 1 �ξ�硢
��(x) �� 1 - x/2 ���Ȥʤ�ޤ����̤ε�����������äƦ�(x)�� 1�Ȥʤ뤳�Ȥϴ�ñ�˳�ǧ�Ǥ��ޤ����ޤ� �̡�(x) �Υƥ��顼�������������ޤ���
- x �� 3/4 �ϲ��߹�ʤΤǡ�-
��̡�(x) �� -
+ 2x/3���ޤ��� -
�� ��' (x) �� 0 �Ȥʤ�Τǡ�|�̡�(x) | ��
�Ȥʤ�ޤ�����
���� 4 ���
- ln ���Ф���ƥ��顼�����
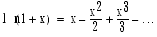
- �ϸ�������0 < x -ln (1 + x) < x2/2 �ʤΤǡ�ln (1 + x) �� x �Ƕ��������Ȥ������и����� x/2 �ˤ���ϰϤ���ޤ�ޤ���1
x = 1 �ξ�硢|x|<�ŤȤʤ�Τǡ����и������ϰϤ� ��/2�Ȥʤ�ޤ���
1
x ��1 �ξ�硢1
x = 1 +
�ˤ�ä�
��������ޤ���0�� x < 1 �ΤȤ���
(1x)
1 =
�Ǥ���
�������п���ulp ������ϰϤǷ�������硢ln (1 + x)/((1 + x) - 1) �μ��η��ͤϼ��Τ褦�ˤʤ�ޤ���
(1 +
1) (1 +
2) =
(1 +
1) (1 +
2) = µ(
) (1 +
1) (1 +
2) (29)
�����ǡ�|��1| �� �� ��|��2| �� �� �Ǥ�����(
��() �γ��������ˤϡ�x ����
�δ֤�����ΦΤ��Ф��ơ�����ʿ���ͤ���������Ѥ��ޤ���
) - ��(x) = (
- x)�̡�(��) (30)
��������顢|
- x| ��ŤȤʤꡢ��������� 13 ���Ȥ߹�碌��ȡ�
|��() - ��(x)|�� ��/2���ޤ��� |��(
)/��(x) - 1| ���/(2|��(x)|)��ŤȤʤ�ޤ������ʤ�� |��3|��Ťξ��˦�(
) = ��(x)(1 +�� 3) �Ȥʤ�ޤ����Ǹ�� x �Ǿ軻����ȡ��ǽ�Ū�� ��4 ��Ƴ�������Τǡ�x��ln (1
x)/((1
x)
1) �ϼ��Τ褦�ˤʤ�ޤ���
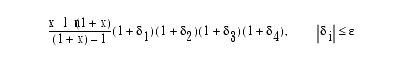
- ��< 0.1 �Ǥ���С� (1 +��1) (1 +��2) (1 +��3) (1 +��4) = 1 +�� (������|��|�� 5�� �ξ��) �Ȥʤ�ޤ�����
���� (19)�� (20)�� (21) ����Ѥ�������ʬ�Ϥζ�̣������ϡ����������κ��θ���
�˸��뤳�Ȥ��Ǥ��ޤ������껦���ǡ�������������뤳�Ȥˤ�ꡢ�ޤ��������ǵ������ǽ���Τ����껦���˽���Ǥ��뤫���ޤ�������������d = b 2 - 4ac �η����˵������ǽ���Τ����껦���⤦ 1 �Ĥ���ޤ��������껦�ϡ�ñ�˸��������촹��������Ǥϼ��������ȤϤǤ��ޤ���ñ�˸����ȡ�b2
4ac �ΤȤ����ݤ�����ˤ�ꡢ���������κ��θ����Ƿ����뺬��Ⱦʬ�η�ޤDZ���������ǽ��������ޤ��������ǡ�ά���ξ������ޤ� (���������κ��θ����θ��������뤿����̤Υ��ץ������� Kahan (1972) �λ����˾Ҳ𤵤�Ƥ��ޤ�)��
b2
4ac �ξ�硢�ݤ�����ˤ�ꡢ���������κ��θ���
�Ƿ����뺬�η��Ⱦʬ�ޤDZ���������ǽ�������롣
(b
b)
(4a
c) = (b2 (1 +��1) - 4ac (1 +��2)) (1+��3) (������ |��i| ���) �Ȥʤ�ޤ���30
d = b2 - 4ac ����Ѥ���ȡ� (d(1 +��1) - 4ac(��2 - ��1)) (1 +��3) �Τ褦�˺ƽ��ߤ���ޤ���
���θ����Υ��������Ѥ��ˤϡ���i ���� 2 ���̵�뤷�ޤ������ξ������и�����
d (��1+��3) - 4ac��4 �Ȥʤ�ޤ� (������ |��4| = |��1-��2|�� 2�ŤǤ�)���Ǥ��뤿�ᡢ�� 1 �� d (��1+��3) ��̵��Ǥ��ޤ���
�� 2 ����Ѥ����ϡ�ax2 + bx + c = a (x - r1) (x - r2) �Ȥ������¤ˤ�ȤŤ���
ar1r2 = c �Ȥʤ�ޤ���b24ac �ξ�硢r1
r2 �Ȥʤ�Τǡ��� 2 �ι��
4ac��44a2 r 1��42 �Ȥʤ�ޤ���
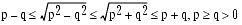
�ϡ�
(������
) �Ǥ��뤳�Ȥ��Τǡ�
a �����������
�Ȥʤꡢ�� r1
r2 �β���Ⱦʬ���˲����ޤ���
��4��-p �ʤΤǡ�
�Ȥʤꡢ���и�����
�ˤʤ�ޤ���
���ʤ����ʿ�����η��Ǥ��η���ȼ�������μ��Ǥ� ri �β���Ⱦʬ���б�������֤˰�̣�Τ���ӥåȤ���Ǽ����ʤ����ᡢri �β��̥ӥåȤ�ͭ�դˤʤ�ޤ���
�Ǹ�ˡ����� 6 �ڤ��Ƥߤޤ�������ϡ������� 14 ������ 8���ι�Ǿ���������¤ˤ�ȤŤ������Ǥ���
���� 14
- 0 < k < p �Ȥ��ơ�m = ��k + 1 �åȤ�����ư�������黻�����Τ˷�������ΤȲ��ꤹ�롣 (m
x)
(m
x
x) ��ͭ�շ� p - k �˴ݤ���Τ� x �Ȥ��Ʒ�����롣��������Τ˸����ȡ��Dz��̷� k �κ��ΰ��֤˴���ݥ���Ȥ����뤳�Ȥ�����ˡ������˴ݤ�뤳�Ȥˤ�ꡢx ��ͭ�շ� x ����Ѥ��ƴݤ���롣
���� 6 ���
- ���� 14 �ˤ�ꡢxh �� p - k =[p/2]�˴ݤ���ޤ������������Ȥ��ʤ���С�xh �� [p/2] ��ͭ�շ��ɽ�魯���Ȥ��Ǥ��ޤ������������Ȥ������硢
x = x0.x1 ... xp - 1 × ��e �Ǥ���С�xp - k - 1 �� 1 ���û�����ޤ������������Ȥ�¸�ߤǤ���Τ� xp - k - 1 =��-1 �ξ������˸¤�졢xh �β��̷�� 1 + xp - k - 1=0 �Ȥʤ�Τǡ�xh �� [p/2] ���ɽ�����뤳�Ȥ��Ǥ��ޤ���- xl ����褦�ˡ� ��p-1 �� x �� ��p -1 �������������� x ���ಽ (��������) ���ޤ���
(������
�� x �ξ�̷� p - k �ǡ�
�ϲ��̷� k) �Ȥ��ޤ���
��θ���٤��������� 3 �Ĥ���ޤ����ξ�硢p - k ��� x ��ݤ�����ϥ���åԥ������ xh =
��xl =
��Ʊ���ˤʤ�ޤ���
�κ����� k �ʤΤǡ�p �������ξ�硢
�κ����� k =[p/2] =[p/2]�Ȥʤ�ޤ���
����ʳ��ξ��ϡ�b = 2�������< 2k-1 �ϡ�ͭ�շ� -1 �� [p/2] ��ɽ�魯���Ȥ��Ǥ��ޤ���2 ���ܤΥ������ϡ�
> (��/2 ) ��k-1 �ξ��ǡ�xh ���������ڤ�夲���Ԥ���Τǡ�xh=
+��k �ˤʤꡢx1 = x - xh = x -
-��k =
-��k �ˤʤ�ޤ���
�κ����� k �ˤʤ�Τǡ�[p/2] ��ɽ���Ǥ��ޤ����Ǹ��
= (��/2 ) ��k-1 �ξ�硢�ڤ�夲��̵ͭ�ˤ�äơ�xh=
���ޤ���
+ ��k �Ȥʤ�ޤ����������äơ�xl �� (��/2 )��k-1���ޤ��� (��/2 ) ��k-1-��k = - ��k/2 �ˤʤꡢ������� 1 ���ɽ�魯���Ȥ��Ǥ��ޤ�����
���� 6 �ˤ�ꡢ2 �Ĥ����٤ο������Τ��¤Ȥ���ɽ�����뤳�Ȥ��Ǥ��ޤ����¤����Τ�ɽ�魯����θ���������ޤ���|x|�� |y|�ΤȤ� x + y = (x
y ) + (x
(x
y) )
y (Dekker 1971��Knuth 1981��Theorem C �� 4.2.2 ��)�����������Τʴݤ�������Ѥ�����硢���θ����ϡ�x = 0.99998�� y = 0.99997 ����˼����Ȥ����= 2 �ξ��˸¤꿿�ˤʤꡢ��= 10 �ˤ�Ŭ�Ѥ���ޤ���
2 �ʿ����� 10 �ʿ��ؤ��Ѵ�
ñ���٤Ǥϡ�p = 24��224 < 108 �ˤʤ�Τǡ�2 �ʿ����� 8 ��� 10 �ʿ����Ѵ����Ƥ⡢��Ȥ� 2 �ʿ��������Ǥ����Τȴ��Ԥ������Ǥ������ºݤˤϤ����Ǥ���ޤ���
���� 15
- 2 �ʤ� IEEE ñ���ٿ���Ǥ�ᤤ 8 ��� 10 �ʿ����Ѵ�������硢ɬ������ 10 �ʿ������Ȥ� 2 �ʿ����դ������Ǥ���櫓�ǤϤʤ�����������9 ��� 10 �ʿ�����Ѥ���С�10 �ʿ�����Ǥ�ᤤ 2 �ʿ��ؤ��Ѵ��ˤ�ꡢ��Ȥ���ư������������������롣
����
- 2 �ʤ�ñ���ٿ���Ⱦʬ�������ֳ� [103, 210) = [1000, 1024) ��¸�ߤ���Τǡ�2 �ʾ������α�¦�ˤ� 10 �ӥåȡ���¦�ˤ� 14 �ӥåȤ����줾���֤���ޤ����������äơ����δֳ֤���˷� (210 - 103)214 = 393,216 �Ĥ� 2 �ʿ���¸�ߤ��뤳�Ȥˤʤ�ޤ���10 �ʿ��� 8 ���ɽ�魯�ȡ�Ʊ���ֳ֤� (210 -103 ) 104 = 240,000 �Ĥ� 10 �ʿ���¸�ߤ��ޤ���240,000 �Ĥ� 10 �ʿ��� 393,216 �Ĥ� 2 �ʿ���ɽ�����뤳�Ȥ��Ǥ��ʤ��Τ����餫�Ǥ����������äơ�ñ���٤� 2 �ʿ����դ�ɽ������ˤϡ�8 ��� 10 �ʿ��Ǥ��Խ�ʬ�Ȥ������Ȥˤʤ�ޤ���
- 9 �夢��н�ʬ�Ǥ���Ȥ������ϡ��� 2 �ʿ��֤δֳ֤��Ĥͤ� 10 �ʿ��ɤ����δֳ֤���礭�����Ȥ����餫�ˤ���С��¾ڤ���ޤ�������ˤ�ꡢ�� 10 �ʿ� N ���Ȥˡ�
- [N -
ulp, N +
ulp] �δֳ֤˺��� 1 �Ĥ� 2 �ʿ����ޤޤ�뤳�Ȥ��ݾڤ���ޤ����������äơ��� 2 �ʿ��Ϥ��줾���դ� 10 �ʿ��˴ݤ���������10 �ʿ��ϰ�դ� 2 �ʿ����Ѵ�����ޤ���
- 2 �ʿ��ɤ����δֳ֤� 10 �ʿ��δֳ֤��Ĥͤ��礭�����Ȥ�������뤿��ˡ� [10n, 10n + 1] �Ȥ����ֳ֤ξ���ͤ��Ƥߤޤ������δֳ֤ξ�硢Ϣ³���� 10 �ʿ��δֳ֤ϡ� 10 (n + 1) - 9 �ˤʤ�ޤ��� [10n, 2m] �� m ���Ǿ������ξ�硢 10n < 2m��
2 �ʿ��ɤ����δֳ֤� 2m - 24 �Ȥʤꡢ���δֳ֤Ϥ������˹����ʤ�ޤ����������äơ�10(n + 1) - 9 < 2m - 24 �Ǥ��뤳�Ȥ��ǧ����н�ʬ�Ȥ������Ȥˤʤ�ޤ����������ºݤˤϡ�10n < 2m �ˤʤ�Τǡ�10(n + 1) - 9 = 10n10-8 < 2m10-8 < 2m2-24 �Ȥʤ�ޤ�����Ʊ�������������٤ξ��ˤ�Ŭ�Ѥ��ơ�17 ��� 10 �ʿ�����Ѥ���С������ٿ����դ������Ǥ��뤳�Ȥ�����Ǥ��ޤ���
2 �ʿ��� 10 �ʿ����Ѵ��ϡ��ե饰�λ��Ѥ˴ؤ�����ˤ�Ŭ�Ѥ���ޤ��������١��ǡ�10 �ʿ��γ�ĥ���� 2 �ʿ�����������ˤϡ�10 �ʿ����� 2 �ʿ��ؤ��Ѵ������Τ˼¹Ԥ��ʤ���Фʤ�ʤ����������ޤ����������Ѵ��ϡ���ĥñ���٥ե����ޥåȤ� N �� 10|P| (������� p < 13 �ξ������Τʿ�) ��褸���塢�����ñ���٤˴ݤ�뤳�Ȥˤ�äƹԤ��ޤ�(p < 0 �ξ��Ͻ����ǡ�������ξ���Ʊ�����) ��N ס�10|P| �η������ΤǤʤ����Ȥϸ����ޤǤ⤢��ޤ���ĥñ���٤���ñ���٤��Ѵ��������Τʴݤ������Ȥ߹�碌����� (N��10|P|) �Ǥ��뤫��Ǥ������Τ���礯��ǽ���Τ�����ͳ�뤿��ˡ���= 10��p = 2 (ñ���٤ξ��) ���ޤ� p = 3 (��ĥñ���٤ξ��) ��ñ��ʥ�������ͤ��Ƥߤޤ����Ѥ� 12.51 �ξ�硢����ϳ�ĥñ���٤ξ軻�� 1 ���Ȥ��� 12.5 �˴ݤ���ޤ���ñ���٤˴ݤ��ȡ�12 �ˤʤ�ޤ������������� 12.51 ��ñ���٤˴ݤ��� 13 �ˤʤ�Τǡ��������������ޤ����θ����������٤ˤ��ݤ�ˤ�äƵ�������ΤǤ���
IEEE �ե饰����Ѥ��뤳�Ȥˤ�ꡢ���������٤δݤ�������뤳�Ȥ��Ǥ��ޤ����ޤ��������Τʥե饰�θ��ߤ��ͤ���¸���ơ������ꥻ�åȤ��ޤ����ݤ�⡼�ɤ�֥����ؤδݤ�פ˥��åȤ��ޤ������θ塢N��10|P| ������ޤ��������Υե饰�ο������ͤ�
ixflag�˳�Ǽ���ơ��ݤ�⡼�ɤ������Υե饰��ꥹ�ȥ����ޤ���ixflag�� 0 �Ǥ���С�N��10|P| �����Τˤʤ�Τǡ�(N��10|P|) ��ǽ��ӥåȤޤ����Τ˴ݤ�ޤ����ޤ�ixflag�� 1 �Ǥ���С��֥����ؤδݤ�פǤ�ɬ���ڤ�ΤƤ��Ԥ���Τǡ��夬����Ƥ����ǽ��������ޤ����Ѥ�ͭ�շ�ϡ�1.b1...b22b23...b31 �Τ褦�ˤʤ�ޤ��������٤δݤ�����ϡ�b23 ...b31 = 10...0 �ξ��˵������ǽ��������ޤ��������Υ������ڤ���ˤϡ�ñ�� b31 ���Ф�ixflag������OR��¹Ԥ��ޤ�������ˤ�� (N��10|P|) �δݤ����ϡ����٤ƤΥ������ˤĤ����������¹Ԥ����褦�ˤʤ�ޤ�����ˡ�θ���
�ֺ�Ŭ���ץ��������Ǥϡ�Ĺ����¤����Τ˷�����Ȥ���������Ŧ���ޤ������������٤�������뤿��κǤ��ñ�ʥ��ץ������ϡ����٤��ܲä��뤳�ȤǤ������٤��ܲä�����̡��¤����٤��ɤ����ٲ�������뤫��������ˡ�s1 = x1��s2 = s1
x2..., si = si - 1
xi �Ȥ��ޤ������ˡ�si = (1 + ��i) (si - 1 + xi) (������|��i | ���) �Ȥ��ơ���i ���� 2 ���̵�뤹��ȡ����μ��������ޤ���
(31)
���� (31) �κǽ�������ˤ�ꡢ
�η��ͤϡ�xj ����ư�ͤ����Τʲ�ˡ��¹Ԥ�������Ʊ���ˤʤ�ޤ����ǽ�ι� x1 �� n�Ťˤ�ä���ư���졢�Ǹ�ι� xn �ϦŤˤ�ä���ư����ޤ������� (31) �� 2 ���ܤ������ϡ��������ϰϤ�
�ˤ�äƵ��ꤵ��뤳�Ȥ���ΤǤ������٤��ܲä���ȡ��Ť���褵��ޤ���IEEE �����٥ե����ޥåȤ��¤����ȡ�1/��
1016 �ˤʤ�Τǡ�n ���������ͤˤĤ���
�Ȥʤ�ޤ���
�������äơ����٤��ܲä���ȡ�n�Ťκ�����ư��Ŭ�Ѥ��졢���ѹ�����ޤ�������ˤ�ꡢKahan �β�ˡ�����˴ؤ��� 2�ŤȤ��������ϰ� (���� 8) �ϡ�ñ���٤���Ϥ뤫�˲���������ΤΡ������٤ξ��ۤɤ����٤������ʤ����Ȥˤʤ�ޤ���
Kahan �β�ˡ������ͭ���ˤʤ���ͳ��狼��䤹���������뤿��ˡ����οޤ˽��äƹͤ��Ƥߤޤ���
��ˡ��¹Ԥ��뤿�Ӥˡ����Υ롼�פ�Ŭ�Ѥ���뷸�� C ����������ޤ����ޤ������Υ롼�פǷ����������� C �� Xj ���鸺�����ơ��������ÿ� Y ����ޤ������ˤ��βÿ��ߤ��¤˲û����ޤ���Y �β��̥ӥå� (���ʤ�� Yl ) ���¤ˤ�������ޤ����� T - S ������ơ�Y �ξ�̥ӥåȤ�����ޤ����������� Y ����ȡ�Y �β��̥ӥåȤ���������ޤ�������ϡ��ޤκǽ���¤Ǽ���줿�ӥåȤ��������ޤ��������ΥӥåȤϡ����Υ롼�פν������ǤȤʤ�ޤ���Knuth ���� (1981) �� 572 �ڡ����ˤ������� 8 �������ʾ����ϡ������� 14 ������ 8���˾Ҳ𤵤�Ƥ��ޤ���
�ޤȤ�
����ԥ塼�������ƥ���߷Ԥ�����ư�������˴ؤ�����ʬ��̵�뤹��Τ����������ȤǤϤ���ޤ������餯������ϥ���ԥ塼���������μ��Ȥ���ư�������ˤĤ��ư������ۤȤ�ɡ����뤤�Ϥޤä����ʤ����Ȥ˵������Ƥ����ΤȻפ��ޤ������Τ��Ȥϡ���ư�����������̲��Ǥ�������ǤϤʤ�����������ä��ϡ��ɥ������䥽�եȥ������ˤĤ��Ƥ��줳������Ω�Ƥ��̣�Ϥʤ��Ȥ��ä�ǧ����븶���ˤ�ʤäƤ��ޤ���
�ܻ����Ǥϡ���ư�������ˤĤ����Ѷ�Ū������Ū�ʸ�Ƥ��ä��뤳�Ȥ���ǽ�Ǥ��뤳�Ȥ�¾ڤ��Ƥ��ޤ������㤨�С��껦��ȼ����ư���������르�ꥺ��ϡ����Ѥ���ϡ��ɥ��������ݸ�����ݤ�����ĥ���٤����ݡ��Ȥ��줿�����β�ǽ�� 2 �ʿ� /10 �ʿ��Ѵ��˴ؤ������Ū�ʥ��르�ꥺ����Ѱդ���С����и�����Ǿ��¤��ޤ��뤳�Ȥ��Ǥ��ޤ������Ѥ��륳��ԥ塼�������ƥ����ư�����������ݡ��Ȥ���Ƥ���С��������Τ�����ư���������եȥ������ι��ۺ�Ȥ������˴��Dz�����ޤ����ܻ����ǾҲ𤷤� 2 �Ĥ��� (�ݸ��ȳ�ĥ����) �ʳ��ˡ��֥����ƥ��¦�̡��Ǥϡ�̿��åȤ��߷פ��饳��ѥ���κ�Ŭ���˻��ޤǡ���ư���������ΨŪ�˥��ݡ��Ȥ��뤿��Τ��ޤ��ޤ����Ҳ𤷤ޤ�����
IEEE ��ư������ɸ�ब������ڤ��Ƥ��뤳�Ȥϡ�ɸ��˽�������ɤΰܿ����������뤳�Ȥ��̣���ޤ�����IEEE ɸ����Ǥϡ�IEEE ɸ��ε�ǽ�����Ѥ��ơ�����Ū����ư�����������ɤ�ɤΤ褦�˵��ҤǤ��뤫�����Ū���������ޤ�����
�ռ�
�ܻ����ϡ�1988 ǯ 5 ��� 7 �Sun Microsystems �Ҥ� David Hough ��ζ��ϤΤ�Ȥ� Sun Microsystems �Ҥdz��Ť��줿 W. Kahan ��ιֵ��ͤ˺���������ΤǤ����ܻ�������Ƥ�ľ�����¡��ʤ�̤����Ϥȵ��Ťʥ����Ȥ������� Kahan ���Xerox PARC �γ��͡��ä� John Gilbert ��ˤϡ��������դΰդ�ɽ�魯��ΤǤ����ޤ� Paul Hilfinger ���Ϥ��ᡢ�ط��ƼԤˤ�¿��ʤ����Ϥ����������Ȥ˴��դ������ޤ���
���ͻ���
Aho, Alfred V., Sethi, R., and Ullman J. D. 1986. Compilers: Principles, Techniques and Tools, Addison-Wesley, Reading, MA.
ANSI 1978. American National Standard Programming Language FORTRAN, ANSI Standard
X3.9-1978, American National Standards Institute, New York, NY.Barnett, David 1987. A Portable Floating-Point Environment, unpublished manuscript.
Brown, W. S. 1981. A Simple but Realistic Model of Floating-Point Computation, ACM Trans. on Math. Software 7(4), pp. 445-480.
Cody, W. J et. al. 1984. A Proposed Radix- and Word-length-independent Standard for Floating-point Arithmetic, IEEE Micro 4(4), pp. 86-100.
Cody, W. J. 1988. Floating-Point Standards -- Theory and Practice, in "Reliability in Computing: the role of interval methods in scientific computing", ed. by Ramon
E. Moore, pp. 99-107, Academic Press, Boston, MA.Coonen, Jerome 1984. Contributions to a Proposed Standard for Binary Floating-Point Arithmetic, PhD Thesis, Univ. of California, Berkeley.
Dekker, T. J. 1971. A Floating-Point Technique for Extending the Available Precision,
Numer. Math. 18(3), pp. 224-242.Demmel, James 1984. Underflow and the Reliability of Numerical Software,
SIAM J. Sci. Stat. Comput. 5(4), pp. 887-919.Farnum, Charles 1988. Compiler Support for Floating-point Computation, Software-Practice and Experience, 18(7), pp. 701-709.
Forsythe, G. E. and Moler, C. B. 1967. Computer Solution of Linear Algebraic Systems,
Prentice-Hall, Englewood Cliffs, NJ.Goldberg, I. Bennett 1967. 27 Bits Are Not Enough for 8-Digit Accuracy, Comm. of the
ACM. 10(2), pp 105-106.Goldberg, David 1990. Computer Arithmetic, in "Computer Architecture: A Quantitative Approach", by David Patterson and John L. Hennessy, Appendix A, Morgan Kaufmann, Los Altos, CA.
Golub, Gene H. and Van Loan, Charles F. 1989. Matrix Computations, 2nd edition,
The Johns Hopkins University Press, Baltimore Maryland.Graham, Ronald L. , Knuth, Donald E. and Patashnik, Oren. 1989. Concrete Mathematics, Addison-Wesley, Reading, MA, p.162.
Hewlett Packard 1982. HP-15C Advanced Functions Handbook.
IEEE 1987. IEEE Standard 754-1985 for Binary Floating-point Arithmetic, IEEE, (1985). Reprinted in SIGPLAN 22(2) pp. 9-25.
Kahan, W. 1972. A Survey Of Error Analysis, in Information Processing 71, Vol 2,
pp. 1214 - 1239 (Ljubljana, Yugoslavia), North Holland, Amsterdam.Kahan, W. 1986. Calculating Area and Angle of a Needle-like Triangle, unpublished manuscript.
Kahan, W. 1987. Branch Cuts for Complex Elementary Functions, in "The State of the Art in Numerical Analysis", ed. by M.J.D. Powell and A. Iserles (Univ of Birmingham, England), Chapter 7, Oxford University Press, New York.
Kahan, W. 1988. Unpublished lectures given at Sun Microsystems, Mountain View, CA.
Kahan, W. and Coonen, Jerome T. 1982. The Near Orthogonality of Syntax, Semantics, and Diagnostics in Numerical Programming Environments, in "The Relationship Between Numerical Computation And Programming Languages", ed. by J. K. Reid, pp. 103-115,
North-Holland, Amsterdam.Kahan, W. and LeBlanc, E. 1985. Anomalies in the IBM Acrith Package, Proc. 7th IEEE Symposium on Computer Arithmetic (Urbana, Illinois), pp. 322-331.
Kernighan, Brian W. and Ritchie, Dennis M. 1978. The C Programming Language,
Prentice-Hall, Englewood Cliffs, NJ.Kirchner, R. and Kulisch, U. 1987. Arithmetic for Vector Processors, Proc. 8th IEEE Symposium on Computer Arithmetic (Como, Italy), pp. 256-269.
Knuth, Donald E., 1981. The Art of Computer Programming, Volume II, Second Edition, Addison-Wesley, Reading, MA.
Kulisch, U. W., and Miranker, W. L. 1986. The Arithmetic of the Digital Computer: A New Approach, SIAM Review 28(1), pp 1-36.
Matula, D. W. and Kornerup, P. 1985. Finite Precision Rational Arithmetic: Slash Number
Systems, IEEE Trans. on Comput. C-34(1), pp 3-18.Nelson, G. 1991. Systems Programming With Modula-3, Prentice-Hall, Englewood Cliffs, NJ.
Reiser, John F. and Knuth, Donald E. 1975. Evading the Drift in Floating-point Addition, Information Processing Letters 3(3), pp 84-87.
Sterbenz, Pat H. 1974. Floating-Point Computation, Prentice-Hall, Englewood Cliffs, NJ.
Swartzlander, Earl E. and Alexopoulos, Aristides G. 1975. The Sign/Logarithm Number System, IEEE Trans. Comput. C-24(12), pp. 1238-1242.
Walther, J. S., 1971. A unified algorithm for elementary functions, Proceedings of the AFIP Spring Joint Computer Conf. 38, pp. 379-385.
���� 14 ������ 8
���ι�Ǥϡ��ܽ�ǰ��äƤ��ʤ�����Ū�ʾ����� 2 �ľҲ𤷤ޤ���
���� 14
- 0 < k < p �Ȥ��ơ�m = ��k + 1 �åȤ�����ư�������黻�����Τ˷�������ΤȲ��ꤹ�롣 (m
x)
(m
x
x) ��ͭ�շ� p - k �˴ݤ���Τ� x �Ȥ��Ʒ�����롣��������Τ˸����ȡ��Dz��̷� k �κ��ΰ��֤˴���ݥ���Ȥ����뤳�Ȥ�����ˡ������˴ݤ�뤳�Ȥˤ�ꡢx ��ͭ�շ� x ����Ѥ��ƴݤ���롣
����
m
- �����μ��ϡ�mx = ��kx + x �η���̤ˤ����륭�������Ȥ�̵ͭ�ˤ�ä� 2 �ĤΥ�������ʬ�����ޤ���
- ���������Ȥ��ʤ����ϡ�x �������ˤʤ�褦�˴�ಽ (��������) ���Ƥ�����Ϥ���ޤ�����ˤ�� mx = x + ��k x �ϼ��Τ褦�ˤʤ�ޤ���
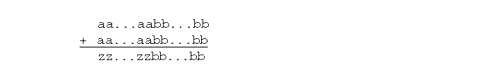
- ������ x �ϡ�2 �Ĥ���ʬ�˶�ʬ����Ƥ��ޤ������̤� k ���
b����̤� p - k ���a��ɽ�路�ޤ���mx ���� mx �������ȡ����̤� k �� (
b��ɽ�路����) ���ݤ���ޤ���x = mx - x mod(��k) + r��k (32)
(m
- r ���ͤϡ�
.bb...b������礭����� 1������ʳ��ξ��� 0 �ˤʤ�ޤ�����̩�˸����ȼ��Τ褦�ˤʤ�ޤ���
a.bb...b�� a + 1 �˴ݤ����� r = 1������ʳ��ξ��� r = 0 (33)- ���� m
x - x = mx - x mod (��k) + r��k - x = ��k(x + r) - x mod (��k) ������ޤ������οޤˡ�m
x - x �η����ݤ���롢�Ĥޤ� (m
x)
x �Ǥ��뤳�Ȥ��ޤ�������ʤ� ��k (x + r) ��ɽ�路�ޤ� (������
B�ϡ��Dz��̷�b��r��ä������η��ɽ�路�ޤ�)��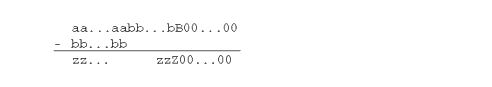
.bb...b<�ξ��� r = 0 �Ȥʤꡢ�����ˤ��
B�η夫��ڤ꤬�����ޤ����������ݤ���뤿��ǽ�Ū�ˤϴݤ�κ������ʤ�Ʊ�������ʤ�� ��kx �Ȥʤ�ޤ���
�ޤ�.bb...b>�ξ��ϡ�r = 1 �Ȥʤꡢ�ڤ�Τ����
B���� 1 �����������̤�Ʊ������kx�Ȥʤ�ޤ���
�Ǹ��.bb...b=�ξ���ͤ��ޤ���r = 0 �ξ�硢
B�϶�����Z�ϴ���Ȥʤꡢ�����ڤ�夲����Τǡ���̤� ��kx �Ȥʤ�ޤ���Ʊ�ͤ� r = 1 �Ǥ���С�B�ϴ����Z�϶����ˤʤꡢ�����ڤ�ΤƤ��ޤ�����̤�Ʊ������kx �Ȥʤ�ޤ����ʾ��ޤȤ��ȼ��Τ褦�ˤʤ�ޤ���x)
x =��kx (34)
- (32) �� (34) �����������Ȥ߹�碌��ȡ� (m
x) - (m
x
x) = x - x mod (��k) + �ѡ���k �Ȥʤ�ޤ�������������ȡ����η�̤������ޤ���
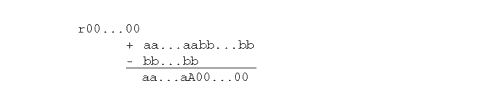
- ������ (33) �� r �������롼��ϡ�
a...ab...b�� p - k ��˴ݤ����Υ롼���Ʊ���Ǥ����������äơ���ư�������黻�����٤� mx - (mx - x) ������뤳�Ȥϡ�x + ��k x �ǥ��������Ȥʤ��ΤȤ��� x �� p - k ��˴ݤ����Ȥޤä����������ʤ�ޤ���- x +��kx �ǥ��������Ȥ�ȼ����硢mx = ��kx + x �ϼ��Τ褦�ˤʤ�ޤ���
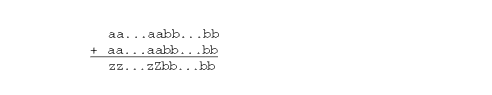
- �������äơ�m
x = mx - x mod (��k) + w��k (������ Z < ��/2 �ξ��� w = -Z) �Ȥʤ�ޤ� (w �����Τ��ͤϽ��פǤϤ���ޤ���) ������ m
x - x = ��kx - x mod (��k) + w��k �ˤʤ�ޤ�����ȼ��Τ褦�ˤʤ�ޤ���
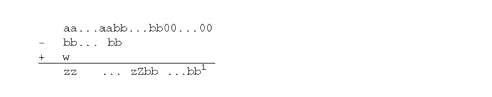
- �����ݤ��� (m
x)
x = ��kx + w��k- r��k (��������
.bb...b>�ξ�硢
�ޤ���.bb...b=�� b0 = 1 �ξ��� r = 1) �Ȥʤ�ޤ�31��
�ޤ� (mx) - (m
x
x) = mx - x mod (��k) + w��k - (��kx + w��k - r��k) = x - x mod(��k) + r��k �Ȥʤ�ޤ������ξ��⡢
a...ab...b�� p - k ��˴ݤ��Ȥ����ڤ�夲��ȼ���ȡ�r = 1 �ˤʤ�ޤ����������äơ������륱�����ˤĤ������� 14 ���������줿���Ȥˤʤ�ޤ��������� 8 (Kahan �β�ˡ���� )
�Υ��르�ꥺ��˽��äƷ����롣
for j = 2 to N {Y = X [j] - C;T = S + Y;C = (T - S) - Y;S = T;}
- ���ΤȤ� S �η��ͤϡ�S =��xj (1 + ��j) + O(N��2) �� |xj| (������ |��j|�� 2��) ���������ʤ롣
����
- �ޤ���ñ��ʸ��� ��xi �θ�����ɤΤ褦�˳������뤫��ͤ��Ƥߤޤ���s 1 = x1��si = (1 +��i) (si-1 +xi) ��Ƴ�����ޤ����¤η��ͤϡ�sn �Ȥʤꡢ����ϳƹ� x ���j �Τ��뼰�Ǿ褸���� xi ���¤��������ޤ���x1 �����Τʷ����� (1+��2)(1+��3) ... (1+��n) �ʤΤǡ��ֹ���ѹ��ˤ�� x 2 �η����ϡ�(1+��3)(1+��4) ... (1+��n) �ˤʤ�ʤ���Фʤ�ޤ������� 8 �ϡ�x1 �η�����¿��ʣ���ˤʤ�����������ޤä���Ʊ���褦�˾������뤳�Ȥ��Ǥ��ޤ���
s0 = c0 = 0 �ǡ����Τ褦�˲��ꤹ��ȡ�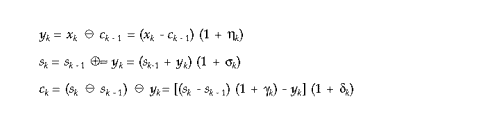
���������嵭�Υ��ꥷ��ʸ���Ϥ��٤ƦŤ��ϰϤ���ޤ�ޤ���sk �� x1 �η����϶�ü�ʼ��Ǥ�����sk - ck �� ck �� x1 �η����������䤹���ʤ�ޤ���k = 1 �ΤȤ������Τ褦�ˤʤ�ޤ���
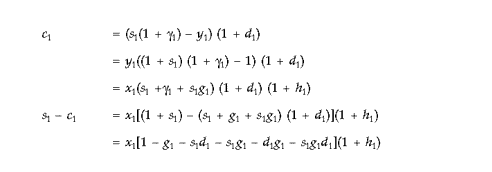
�ʾ�μ��Dz��ˡ�x1 �η����줾�� Ck �� Sk �Ȥ���ȡ����Τ褦�ˤʤ�ޤ���
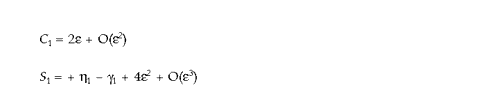
Sk �� Ck �θ�����������褦�ˡ�i > 1 �ξ��� xi ��ȼ����٤�̵�뤷�ơ�Sk �� Ck ��������ĥ���ޤ�����̤ϼ��ΤȤ���Ǥ���
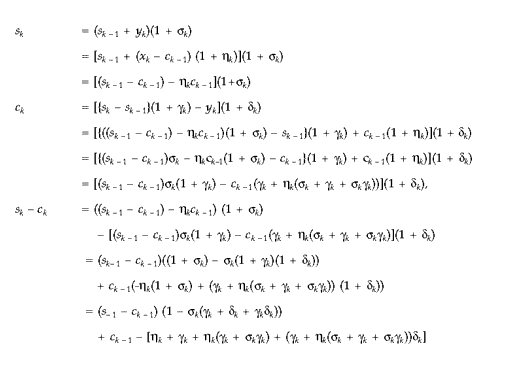
Sk �� Ck �Ϧ�2 �ΰ̤ޤǤ���������ʤ��Τǡ������θ����ϼ��Τ褦�˴�ά���Ǥ��ޤ���
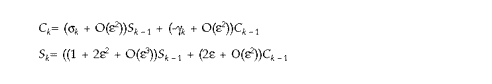
�����μ�����Ѥ���ȡ����Τ褦�ˤʤ�ޤ���
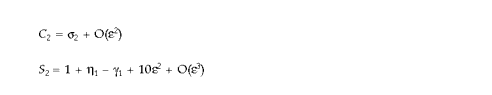
���̤˼��Τ褦�˵�Ǽˡ�ǥ����å�����ȴ�ñ�Ǥ���
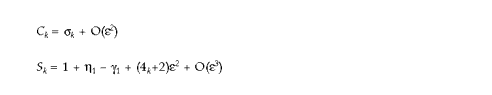
�ǽ�Ū�� sk �� x1 �η�����ɬ�פˤʤ�ޤ��������ͤ�����ˤϡ�xn + 1 = 0 �Ȥ���n + 1 �Ȥ���ź�������դ������ꥷ��ʸ���٤� 0 �Ȥ��� sn + 1 ������ޤ���
���η�̡�sn + 1 = sn - cn �Ȥʤꡢsn �� x 1 �η����� sn + 1 �η�����꾮�����ʤ�ޤ������η����ϡ�sn = 1 +��1 - ��1 + (4n + 2)��2 = (1 + 2�� + O(n��2)) �Ȥʤ�ޤ�����IEEE 754 �����֤ΰ㤤
�� - ������ϡ�ȯ�Ԥ��줿��ʸ�ΰ����ǤϤ���ޤ�������ϡ�IEEE ���ʤΰ��������������ɼԤ���ʸ������̤��䤹�� IEEE �ˤĤ��Ƥλפ��㤤������������ɲä��줿��ΤǤ������λ����� David Goldberg �ˤ�äƵ��Ҥ��줿��ΤǤϤ���ޤ���Goldberg ��ε��Ĥ����Ƥ����˴ޤ���Ƥ��ޤ���
��������ʸ�ϡ��ץ�����ޤϥץ������������٤���ư�������黻����������뤳�Ȥ����뤿�ᡢ��ư�������黻�Ͻ�ʬ�����դ�ʧ�äƼ������ʤ���Фʤ�ʤ����Ȥ��Ƥ��ޤ���IEEE ���ʤ����տ����������ꤷ�Ƥ��ꡢ������ư��������ʥץ�������������Ƥ��ε��ʤ˽�������ƥ�ˤΤ����Τʷ�̤����ۤ��뤳�Ȥϲ�ǽ�Ǥ������Τ褦�ʥץ������Ϥ��٤Ƥ� IEEE �����ƥ�˰ܿ��Ǥ��ʤ���Фʤ�ʤ����ɼԤϷ����դ��뤫�⤷��ޤ��ºݡ�197�ڡ����Ρ֤���ޥ����̤Υޥ���˥ץ�������ܿ�����Ȥ��ˡ�ξ���Υޥ���� IEEE ɸ�ब���ݡ��Ȥ���Ƥ���С����δ֤������������ַ�̤Ϥ��٤ƥ��եȥ������Х��˸��������ꡢ�黻��κ��ˤ���ΤǤʤ��פȤ����긫�����¤Ǥ���ʤ顢�ܿ����Τ��륽�եȥ������ε��Ҥ����Ū��ñ�Ǥ��礦��
��ǰ�ʤ��� IEEE ���ʤϡ�Ʊ��Υץ�����ब IEEE ���Τ��٤ƤΥ����ƥ�Ǥޤä���Ʊ����̤�Ф��Ȥ��ݾڤ��Ƥ��ޤ��ºݡ����ޤ��ޤ���ͳ���顢�ۤȤ�ɤΥץ������ϥ����ƥ�ˤ�äưۤʤä���̤�Ф��ޤ���������ȡ��ۤȤ�ɤΥץ������� 10 �ʷ����� 2 �ʷ����δ֤ǿ��ͤ��Ѵ�������ɬ�פ�����ޤ�����IEEE ���ʤϤ����Ѵ���Ԥ�����������٤����ˤϻ��ꤷ�Ƥ��ޤ��ޤ���¿���Υץ������ϥ����ƥ�饤�֥��ˤ�äƶ��뤵�����ܴؿ�����Ѥ��ޤ�����IEEE ���ʤϤ����δؿ��ˤĤ��ƤϤޤä������ꤷ�Ƥ��ޤ����������ۤȤ�ɤΥץ�����ޤϤ����ε�ǽ�� IEEE ���ʤ��ϰϳ��Ǥ��뤳�Ȥ�ǧ�����Ƥ��ޤ���
IEEE ���ʤ˵��ꤵ�줿���ͷ����ȱ黻��������Ѥ���ץ������Ǥ��顢�����ƥ�ˤ�äưۤʤ��̤�Ф���礬���뤳�Ȥ˵��Ť��Ƥ��ʤ��ץ�����ޤ�¿�����ȤǤ��礦���ºݡ�IEEE ���ʤμ�ɮ�Ԥϡ��ۤʤ�������ۤʤ��̤����ळ�Ȥ�ǧ��ޤ���������ϡ����˼��� IEEE 754 ���ʤ��Ѹ�������פ���������餫�Ǥ� ���ְ���ϡ��桼�����ˤ�ä�����Ū�˻��ꤵ��뤫�������ƥ�ˤ����ۤ˶��뤵��� (���Ȥ��С��ץ���������Υ��֥������ץ�å���������ˤ�������ַ��)������ˤ�äƤϡ���ַ��η�̤�桼��������εڤФʤ�������֤���Τ⤢�뤬�������ʤϱ黻��̤���η����ȥ��ڥ��ɤ��ͤˤ�ä�������롣��(IEEE 754-1985��7 �ڡ���) �Ĥޤ� IEEE ���ʤϳƷ�̤ΰ�������٤��������ݤ�뤳�Ȥ��ꤷ�Ƥ��ޤ��������ΰ�������٤�桼�����Υץ������Ƿ��ꤹ��Ȥϵ��ꤷ�Ƥ��ޤ��������äơ��ƥ����ƥ���ȼ������٤Ƿ�̤�������ۤǤ��뤿�ᡢ�����ƥब���٤� IEEE ���ʤ˽�Ƥ��Ƥ⡢Ʊ��Υץ������ǰۤʤ��̤��ФƤ��ޤ��ޤ� (�Ȥ��ɤ��������٤��������ʤ�ޤ�)��
��������ʸ�˼����줿�����Ĥ�����ϡ���ư�������黻�δݤ�˴ؤ����μ�������ˤ��Ƥ��ޤ������Τ褦�������ߤˤ���ˤϡ��ץ�����ޤϥץ�����ब�ɤΤ褦�˲�ᤵ��뤫 (����Ū�� IEEE �����ƥ�Ǥϳƻ��ѱ黻�ΰ�������١ˤ�ͽ¬����ɬ�פ�����ޤ������ȡ�IEEE ���ʤΡ�����������ϡ����ζ��֤ǥץ�����ब�ɤΤ褦�˲�ᤵ��뤫��ǧ������ץ�����ޤ�ǽ�Ϥ��ɤ뤬���Ƥ��ޤ������η�̡���������Τ����Ĥ��ϡ���������ǰ츫�ܿ���ǽ�ʥץ������Ȥ��Ƽ���������硢�̾�ץ�����ޤ�ͽ�������ΤȤϰۤʤ����٤ǰ���˷�̤����ۤ��� IEEE �����ƥ�Ǥ�������ư��ʤ���礬����ޤ���������ư����Τ⤢�뤫�⤷��ޤ���������ư�ʿ��Ū�ʥץ�����ޤ�ǽ�Ϥ�Ķ�����礬����ޤ���
������Ǥϡ�IEEE 754 �黻���̾���Ѥ��밸����������٤˴�Ť��� IEEE 754 �黻�δ�¸�μ����ˤĤ���ʬ�ष�ޤ������Τ��Ȥǡ���ʸ�ΰ����������夲���ץ�����बͽ���������٤�������٤Ƿ�̤����ۤ���ȡ�ͽ�����줿���٤����Ѥ����Ȥ��ˤ��������Ϥ��Ǥ⡢�ְ�ä���̤�����������礬���뤳�Ȥ��ޤ����ޤ�����ʸ��ξ����� 1 �Ĥ�ƹͤ��ơ�ͽ�����ʤ����٤˼���Ȥ� (�������٤��ץ�������̵���ˤ��ʤ��ˤ���) �����ɬ�פ����Ϥ��ޤ�����������ϡ�IEEE ���ʤΤ����뵬��ˤ⤫����餺��IEEE ���ʤ�ǧ���ۤʤ�����֤����Τ���ˡ�ư����Τ�ͽ¬�Ǥ����ܿ���ǽ�Ǹ�ΨŪ�Ǥ���Ȥ������ͥ��եȥ������ҤǤ��ʤ���礬���뤳�Ȥ��Ƥ��ޤ������Τ褦�ʥ��եȥ�������ȯ����ˤϡ�IEEE ���ʤ�ǧ��Ƥ�������������¤���ȤȤ�ˡ��ץ�����ब��¸������ư��������̣����ץ�����ޤ�ɽ���Ǥ���ץ�����ߥ���ȴĶ���ޤ���������ɬ�פ�����ޤ���
���ߤ� IEEE 754 ����
IEEE 754 �黻�θ��ߤμ����ϡ��ϡ��ɥ�������Ǥ���餬���ݡ��Ȥ���Ƽ����ư���������������٤ˤ�� 2 �ĤΥ��롼�פ�ʬ���뤳�Ȥ��Ǥ��ޤ���Intel x86 �ե��ߥ�Υץ����å�����ɽ��������ĥ�١����ץ����ƥ�ϳ�ĥ�����ٷ�����ե륵�ݡ��Ȥ��ޤ�����ñ���٤������٤ˤĤ��Ƥ���ʬŪ�ˤ������ݡ��Ȥ��ޤ���ĥ�١��������ƥ�ϡ�ñ���٤������٤ǥǡ������ɤ߹��ߤȳ�Ǽ��Ԥ����ǡ������ĥ�����ٷ����Ȥδ֤Ǥ��Ф䤯�Ѵ�����̿������ޤ������Υ����ƥ�Ϥޤ�����ĥ�����ٷ����ǥ쥸�������ݻ��������Ǥ�ѱ黻�η�̤�ñ���٤ޤ��������٤˴ݤ���롢�ǥե���ȤȤ��̤��ü�ʥ⡼�ɤ����ޤ���Motorola 68000 ������ץ����å��ϡ���̤��Υ⡼�ɤ�ñ���ٷ����ޤ��������ٷ��������٤��ϰϤ�ξ���˴ݤ�ޤ���Intel x86 ����Ӹߴ��ץ����å��ϡ�ñ���٤ޤ��������ٷ��������٤˷�̤�ݤ�ޤ�����Ʊ���ϰϤ��ĥ�����ٷ����Ȥ����ݻ����ޤ����ۤȤ�ɤ� RISC �ץ����å���ޤ�ñ���٤���������������ƥ�ϡ�ñ���ٷ����������ٷ�����ե륵�ݡ��Ȥ��ޤ�����IEEE ���γ�ĥ�����ٷ����ϥ��ݡ��Ȥ��ޤ���IBM POWER �������ƥ������ñ���٤ˤĤ��Ƥ���ʬŪ�ʥ��ݡ��Ȥ������Ƥ��ޤ���������Ǥ�ñ���� / �����٥����ƥ�Ȥ���ʬ�ष�ޤ���
��ĥ�١��������ƥ�ˤ�����黻ư�ñ���� / �����٥����ƥ�ˤ�����ư��Ȥɤ��ۤʤ뤫���ǧ���뤿��ˡ�212�ڡ����� C �ˤ�����ͤ��Ƥߤޤ���
int main() {double q;q = 3.0/7.0;if (q == 3.0/7.0) printf("Equal\n");else printf("Not Equal\n");return 0;}������Ǥϡ���� 3.0 �� 7.0 �������٤���ư���������Ȥ��Ʋ�ᤵ��Ƥ��ꡢ�� 3.0/
7.0 �ϡ��ǡ�����double��Ѿ����ޤ���ñ���� / �����٥����ƥ�Ǥϡ����Ѥ����������٤���äȤ��ΨŪ�ʷ����Ǥ��뤿�ᡢ���μ��������٤�ɾ������ޤ������Τ��ᡢ�����٤��������ݤ��줿�� 3.0/7.0 ��q����������ޤ������ιԤǡ��� 3.0/7.0 �ϺƤ������٤�ɾ������ޤ������η�̤�����q�����������Ф�����ͤ����������ᡢ�ץ�������ͽ¬�ɤ����Equal�פȽ��Ϥ��ޤ�����ĥ�١��������ƥ�Ǥϼ� 3.0/7.0 �η���
double�ξ��Ǥ⡢���ϥ쥸������dz�ĥ�����ٷ����� (�Ĥޤ�ǥե���ȥ⡼�ɤ�) �����졢��ĥ�����٤˴ݤ���ޤ�������������̤��ͤ��ѿ�q�����������ݤˤ����ͤϥ���˳�Ǽ���졢q��double���������Ƥ��뤿����ͤ������٤˴ݤ���ޤ������ιԤǡ��� 3.0/7.0 �ϺƤӳ�ĥ���٤�ɾ������뤳�Ȥ����ꡢ���ξ��ˤ�q�˳�Ǽ����Ƥ��������٤��ͤȤϰۤʤ��̤����������ץ������ϡ�Not equal�פȽ��Ϥ��ޤ����������ۤ��ν��Ϥ�ͤ����ޤ�������ѥ���ϡ�2 ���ܤιԤǼ� 3.0/7.0 ���ͤγ�Ǽ�ȴݤ��Ԥä���Ǥ����q����Ӥ��뤳�Ȥ⡢�ͤ��Ǽ�����˥쥸�����˳�ĥ���٤�q���ݻ����뤳�Ȥ�Ǥ��ޤ�����Ŭ������ѥ���ϡ�����ѥ�����˼� 3.0/7.0 �������٤�ɾ�����뤳�Ȥ��ĥ�����٤�ɾ�����뤳�Ȥ�ͤ����ޤ� (1 �Ĥ� x86 ����ѥ���ˤ����ơ���Ŭ���ˤ�ꥳ��ѥ��뤹��Ȥ��˥ץ������ϡ�Equal�פȽ��Ϥ����ǥХå��Τ���˥���ѥ��뤹��Ȥ��ϡ�Not Equal�פȽ��Ϥ��ޤ�)����ĥ�١��������ƥ��ѤΥ���ѥ������ˤϡ��ݤ����٥⡼�ɤ�ưŪ���ѹ������쥸������˷�̤���������黻�ˤ�äƷ�̤� (��깭���ϰϤ���Ѥ���) ñ���٤ޤ��������٤˴ݤ���Τ⤢��ޤ������Τ��ᡢ���Τ褦�ʥ����ƥ�Ǥϡ����Υ����������ɤ��ɤ�� IEEE 754 �黻�δ���Ū�ʲ���Ŭ�Ѥ�������Ǥϡ��ץ�������ư���ͽ¬�Ǥ��ޤ��䤿���ϡ��ϡ��ɥ������䥳��ѥ��餬 IEEE 754 ���δĶ������ʤ�����Ȥ��ä��դ�뤳�ȤϤǤ��ޤ��ϡ��ɥ������ϡ�������Ȥ��ꡢ���Τ˴ݤ��줿��̤줾��ΰ�������ۤ��Ƥ��ޤ�������ѥ���ϡ����Ĥ���Ƥ���Ȥ��ꡢ�桼����������εڤФʤ��������ַ�̤��������Ƥ��ޤ�����ĥ�١��������ƥ�ˤ�����黻����Ȥ���
���ְ��̤���ǰ�Ǥϡ���ĥ�١��������ƥ�ϡ�ñ���� / �����٥����ƥ�����ۤ�����̤�����ΤȤϸ����ʤ��Ƥ⡢��������Τʷ�̤��������ʤ���Фʤ�ʤ��Ȥ���Ƥ��ޤ�������ϡ���ĥ�١��������ƥब��˾��ʤ��Ƥ�ñ���� / �����٥����ƥ��Ʊ�������٤����Ƥ��ꡢñ���� / �����٥����ƥ��Ķ���������٤��������¿������Ǥ��������� C �ץ������Τ褦��ñ������ʲ�������������˴�Ť������Ū��̯�ʥץ������ϡ�������ǰ�����������������Ǥ��뤳�Ȥ��Ƥ��ޤ���ñ���� / �����٥����ƥ�ˤϳΤ��˰ܿ��Ǥ���褦�ʡ���������ܿ����Τ���ץ���������ˤϡ���ĥ�١��������ƥ�Ǥ����餫�������Τʷ�̤�Ф���Τ�����ޤ�������ϡ�����ѥ���ȥϡ��ɥ������������ޥץ�����ब���Ԥ���ʾ�����٤����褦�Ȥ��뤿��Ǥ���
���ߤγƼ�Υץ�����ߥ���Ǥϡ��ץ�����ब���Ԥ������٤���ꤹ�뤳�Ȥ�����Ǥ����ָ���ȥ���ѥ��������ǿ���Ƥ���褦�ˡ�¿���Υץ�����ߥ���ϡ�Ʊ������ƥ��������
10.0*x�Τ褦�ʼ���ȯ�����뤴�Ȥˤ���餬Ʊ���ͤ�ɾ������ʤ���Фʤ�ʤ��Ȥϻ��ꤷ�Ƥ��ޤ���Ada �ʤɰ����θ���ϡ��������ˤĤ��� IEEE ���ʰ����Τ��ޤ��ޤʱ黻�ˤ�����Хꥨ�������αƶ�������Ƥ��ޤ�������˿����� ANSI C �Τ褦�ʸ���ϡ�ɸ����γ�ĥ�١��������ƥ�˱ƶ�������Ƥ��ޤ����º� ANSI C ɸ��ϡ�����ѥ��餬��ư�����������̾綠�μ�����б��Ť����Ƥ������٤�������٤�ɾ�����뤳�Ȥ����Τ˵��Ĥ��Ƥ��ޤ������η�̡���10.0*x���ͤϡ����Τ褦�ʤ��ޤ��ޤ��װ��ˤ�äưۤʤ�ޤ���-- ���μ����ѿ��ˤ����������������Τ�������Ȥ����礭�ʼ��ΰ����Ȥ���ɽ�������Τ���������Ӥ˴ط����뤫�ɤ��������������Ȥ��ƴؿ����Ϥ���뤫�ɤ������ޤ��Ϥ�����硢�������ͤȻ��ȤΤɤ���Ȥ����Ϥ���뤫�����ߤ����٥⡼�ɡ��ץ������Υ���ѥ���˻��Ѥ��줿��Ŭ���Υ�٥롢�ץ������Υ���ѥ�����˥���ѥ��餬���Ѥ������٥⡼�ɤȼ���ɾ����ˡ�ʤɡ�ͽ¬�ΤĤ��ʤ�����ɾ���ϡ����쵬�ʤˤ��٤Ƥθ���������櫓�ǤϤ���ޤ���ĥ�١��������ƥ�ϡ���ǽ�ʤ����꼰����ĥ���٥쥸������ɾ���������ˤ�äȤ��Ψ�褯ư��ޤ�������������Ǽ��ɬ�פ��ͤϡ��ᤵ����äȤⶹ�����٤dz�Ǽ����ޤ���
10.0*x����������֤�Ʊ���ͤ�ɾ�������褦�˸�����ᤵ����ȡ������Υ����ƥ�ǥѥե����ޥ��㲼�Ȥ����ڥʥ�ƥ������ʤ��ʤ�ޤ�����ǰ�ʤ��顢��ʸ��Ʊ������ƥ����Ȥ�10.0*x���̤��ͤ�ɾ�����뤳�Ȥ��Υ����ƥ�˵����ȡ����켫�ΤΥڥʥ�ƥ������Τʿ��ͥ��եȥ�������ȯ����ץ�����ޤˤ����ꡢ�տޤ����̣����ɽ�����뤿��˥ץ������ι�ʸ����뤳�Ȥ��Ǥ��ʤ��ʤ�ޤ����ºݤΥץ������ϡ����ꤵ�줿���Ͼ��Ʊ���ͤ�ɾ�������Ȥ����������äƤ���ΤǤ��礦����ln(1 + x) ����������� 4 �Ǽ����줿���르�ꥺ���פ��Ф��Ƥ������������ˡ�FORTRAN �ˤ�뵭�Ҥ��ޤ���
��ĥ�١��������ƥ�Ǥϡ�����ѥ���� 3 ���ܤμ�
1.0 + x���ĥ���٤�ɾ���������η�̤�1.0����ӤǤ��ޤ���������������Ʊ������ 6 ���ܤ� log �ؿ����Ϥ����Ȥ�������ѥ���Ϥ����ͤ����˳�Ǽ���ơ��ͤ�ñ���٤˴ݤ�뤳�Ȥ��Ǥ��ޤ������Τ��� x �Υ�����������ĥ���٤�1.0 + x��1.0�˴ݤ����ۤɾ������ʤ�����ñ���٤Ǥ�1.0 + x��1.0�˴ݤ���뤯�餤�������Ȥ�����硢log1p(x)���֤��ͤ� x �ǤϤʤ������ˤʤꡢ���и����� 1 �ˤʤ�ޤ� (5e ���⤤���֤��礭��)��Ʊ�ͤˡ����֥������ץ�å����1.0 + x���ƻ��ꤵ��Ƥ��� 6 ���ܤμ��λĤ���ʬ����ĥ���٤�ɾ������뤳�Ȥ����ꤷ�ޤ������ξ�硢x������������1.0 + x��ñ���٤�1.0�˴ݤ����ۤɤˤϾ������ʤ��Ȥ����Ȥ���log1p(x)���֤��ͤ��������ͤ����礭���ʤ�ޤ������κ���x�Ȥۤ�Ʊ���ǡ����и����Ϥ��ξ��� 1 �˶�Ť��ޤ�������Ū����Ȥ��ơ�x�� 2-24 + 2-47 �����ꤷ�ޤ����Ĥޤ�x�ϡ�1.0 + x�������礭�ʿ��� 1 + 2-23 �˴ݤ����褦�ʺǾ���ñ���ٿ��Ǥ������ξ�硢log(1.0 + x)�Ϥ��褽 2-23 �Ǥ���6 ���ܤμ���ʬ��ϳ�ĥ���٤�ɾ������뤿�ᡢ���Τ˷������x�����ۤ��ޤ������Τ���log1p(x)�����Τ��ͤΤۤ� 2 �ܤˤ����뤪�褽 2-23 ���֤��ޤ������Τ褦�ʾ����ϡ����ʤ��Ȥ� 1 �ĤΥ���ѥ����ȯ�����ޤ��������Υ����ɤ� x86 �����ƥ��Ѥ� Sun WorkShop Compiler 4.2.1 FORTRAN 77 ����ѥ����-O��Ŭ���ե饰����Ѥ��ƥ���ѥ��뤵����硢�������줿�����ɤ�1.0 + x��嵭�ΤȤ���˷����ޤ������η�̡����δؿ���log1p(1.0e-10)�˥��������ۤ���log1p(5.97e-8)��1.19209E-07�����ۤ��ޤ������� 4 �Υ��르�ꥺ�ब������ư��뤿��ˤϡ���
1.0 + x�Ͻи����뤿�Ӥ�Ʊ����ˡ��ɾ������ʤ���Фʤ�ޤ����Υ��르�ꥺ��ϡ�1.0 + x������Ȥ��ϳ�ĥ�����٤�ɾ�����졢����Ȥ���ñ���٤������٤�ɾ�������Ȥ����褦�˰���Ǥʤ�����������ĥ�١��������ƥ����������̤�Ф��ޤ���log�� FORTRAN �������Ȥ߹��ߴؿ��Ǥ��뤿�ᡢ��������ѥ���ϼ�1.0 + x�ϳ�ĥ���٤�ɾ�����Ƥ����п���Ʊ�����٤Ƿ��Ǥ��ޤ���������ѥ��餬���Τ褦�˼¹Ԥ���ȷ��Ƥ����뤳�ȤϤǤ��ޤ��� (�桼��������δؿ�����Ѥ��������ξ�硢�ؿ���ñ���٤η�̤��֤����Ǥ⥳��ѥ���ϳ�ĥ���٤ǰ������ݻ��Ǥ��ޤ������������⤷¸�ߤ����Ȥ��Ƥ⡢�����¹Ԥ��� FORTRAN ����ѥ���ϤۤȤ�ɤ���ޤ���)�����Τ��ᡢ1.0 + x���ѿ����������뤳�Ȥˤ�ꡢ���μ�����Ʊ���褦��ɾ�������褦�ȥץ�����ޤϻ�ߤ뤫�⤷��ޤ���ǰ�ʤ��顢�ѿ�real���������ȡ������ѿ����ĥ���٤ǥ쥸�����˳�Ǽ����Ƥ����ͤ��ִ������̤��ѿ���ñ���٤ǥ���˳�Ǽ����Ƥ����ͤ��ִ�����褦�ʥ���ѥ����������礬����ޤ��������ǡ���ĥ���ٷ������б����뷿���ѿ����������ɬ�פ�����ޤ���ɸ�� FORTRAN 77 �ϡ����Τ褦����ˡ�����Ƥ��ޤ���FORTRAN 95 �ϳƼ�η�����ɽ������SELECTED_REAL_KIND�ᥫ�˥�������Ƥ��ޤ������ѿ�����ĥ���٤���������褦�˳�ĥ���٤Ǽ���ɾ�����������Ϥä���Ȥϵ��ꤷ�Ƥ��ޤ��Ĥޤꡢɸ��� FORTRAN �ˤϡ���1.0 + x���䤿���ξ�����̵���ˤ��Ƥ��ޤ���ˡ��ɾ������뤳�Ȥ�μ¤��ɤ��褦�ʲ������Τ�����ˡ�Ϥ���ޤ�����ĥ�١��������ƥ�Ǥϡ��ƥ��֥������ץ�å����Ǽ���졢�������ä�Ʊ�����٤˴ݤ���Ƥ�����Ǥ⡢��ư����㤬�ۤ��ˤ⤢��ޤ�����������Ťδݤ��Ǥ����ǥե���Ȥ����٥⡼�ɤǤϡ���ĥ�١��������ƥ�Ͻ��ˤ��줾��η�̤��ĥ�����٤˴ݤ�ޤ������θ夳�η�̤������٤˳�Ǽ�������ˤϡ��ƤӴݤ�Ԥ��ޤ������� 2 �٤δݤ���Ȥ߹�碌�ˤ�ꡢ�ǽ�η�̤������������٤˴ݤ��Ȥ����������ͤȤϰۤʤ��ͤ���������뤳�Ȥ�����ޤ�������ϡ���ĥ�����٤˴ݤ��줿��̤�������͡�(2 �Ĥ������ٿ��Τ��礦�����) �Ǥ��뤿�ᡢ 2 �٤�δݤ��������˴ݤ�뵬§�ˤ�äƷ��ꤵ�����˵����ޤ������� 2 ���ܤδݤ�ǽ�δݤ��Ʊ�������ǹԤ����硢�ǽ�Ū�ʴݤ�����Ϻǽ���Υ�˥åȤ�Ⱦʬ��Ķ���ޤ�������������Ťδݤ�������ٱ黻�ˤ����ƶ���Ϳ���ޤ����� q �ӥåȤ˴ݤ��졢³���� p �ӥåȤ˴ݤ����褦�ʡ�2 �Ĥ� p �ӥåȿ��ͤι�ס������ѡ��ޤ��Ͼ������뤤�� p �ӥåȿ��ͤ�ʿ�����ϡ�q �� 2p + 2 �ξ�硢��̤��������� 1 �٤����� p �ӥåȤ˴ݤ��줿���Τ褦��Ʊ���ͤ��������뤳�Ȥ��狼��ޤ�����ĥ�����٤Ͻ�ʬ�������ᡢñ���ٱ黻����Ťδݤ������뤳�Ȥ�����ޤ���
���Τʴݤ������Ȥ��륢�르�ꥺ�����ˤϡ���Ťδݤ���б��Ǥ��ʤ���Τ⤢��ޤ����ºݡ����Τʴݤ��ɬ�פȤ��� IEEE 754 �˽�ʤ����ޤ��ޤʥޥ����������ư���褦�ʥ��르�ꥺ��Ǥ���Ťδݤ��ư��ʤ��ʤ��礬����ޤ�����������Ǥ�äȤ������ʤΤϡ�189�ڡ����ǿ���Ƥ��륷�ߥ�졼�Ȥ��줿¿�����ٱ黻��¹Ԥ��뤿��ΰܿ����Τ��륢�르�ꥺ��Ǥ������Ȥ��С���ư�����������̤Ȳ��̤���ʬ��ʬ�䤹�뤿������� 6 �ǽҤ٤�줿��ˡ�ϡ���Ťδݤ�黻�Ǥ�������ư��ޤ��������ٿ� 252 + 3 x 226 - 1 ���줾����� 26 �ӥåȤ� 2 �Ĥ���ʬ��ʬ�䤷�ƤߤƤ������������줾��α黻�������٤��������ݤ���Ȥ�����̤���ʬ�� 252 + 227 �Ȥʤ겼�̤���ʬ�� 226 - 1 �Ȥʤ�ޤ��������줾��α黻�����˳�ĥ�����٤˴ݤ���³���������٤˴ݤ����Ȥ��������ʬ�Ȥ��� 252 + 228��������ʬ�Ȥ��� -226 - 1 ����������ޤ���-226 - 1 �� 27 �ӥåȤ�ɬ�פȤ��뤿�ᡢ�������������٤Ǥ����Τ˷��Ǥ��ޤ���������ο��ͤ������ĥ�����٤Ƿ����뤳�Ȥϲ�ǽ�Ǥ��������η�����ޤ�륢�르�ꥺ���ñ���� / �����٥����ƥ�ˤϰܿ��Ǥ��ޤ��ޤ���¿�����٤ξ軻���르�ꥺ��ˤ�뤽�θ�Υ��ƥåפϡ����٤Ƥ���ʬ�Ѥ������٤Ƿ�����Ƥ��뤳�Ȥ�����Ȥ��ޤ����������ѿ��ȳ�ĥ�������ѿ����Ȥ߹�碌�����Τ˽�������ˤϡ������μ�֤������������ޤ���
Ʊ�ͤˡ��������ͤ�����Ȥ���ɽ�������¿�������ͤ�ä���ܿ����Τ��륢�르�ꥺ��ϡ���Ť˴ݤ��Ԥ��黻�Ǥϼ��Ԥ��뤳�Ȥ�����ޤ������Τ褦�ʥ��르�ꥺ��ϡ��̾�Kahan �β�ˡ���������������ˡ����äƤ��ޤ���239�ڡ����˵�줿����ˡ�������ñ�˼������ޤ���狼��褦�ˡ�
s��y��|s| �� |y|�Ǥ�����ư�������ѿ��Ǥ��ꡢ���η���¹Ԥ����硢�ۤȤ�ɤα黻�ˤ�����e��t�η���ȯ�������ݤ���������Τ˲��������ޤ���
���������μ�ˡ�ϡ���Ť˴ݤ����黻�Ǥ�̵���Ǥ���
s= 252 + 1��y= 1/2 - 2-54 �ξ�硢s + y�Ͻ��˳�ĥ�����٤� 252 + 3/2 �˴ݤ��졢����˷�������˴ݤ�뵬§�ˤ�ä������٤� 252 + 2 �˴ݤ���ޤ����������ä�t�η��ˤ�����ǽ�Ū�ʴݤ������ 1/2 + 2-54 �Ǥ�������ϡ������٤����Τ�ɽ�����뤳�Ȥ��Բ�ǽ�Ǥ��ꡢ���Τ���嵭�μ��Ǥ����Τ˷��Ǥ��ޤ����ξ��⡢��ĥ�����٤Τޤ�פ�����뤳�Ȥˤ��ݤ����������Ǥ��ޤ����������ʤ�ȥץ������Ϻǽ����Ϥ餷�������٤��᤹��Ȥ�Ԥ�ɬ�פ����ꡢ��Ťδݤ���Υץ�������Ǻ�ޤ���ǽ��������ޤ������Τ褦����ͳ���顢��������ˡ�ˤ��¿�����ٱ黻�Υ��ߥ�졼�Ȥ�Ԥ��ܿ����Τ���ץ�������¿�ͤʥޥ������������ΨŪ��ư��ޤ�������ĥ�١��������ƥ�Ǥϸ�ɽ�ɤ���ˤ�ư��ޤ����츫���Τʴݤ�˰�¸���Ƥ���褦�ʥ��르�ꥺ��Ǥ⡢�ºݤ���Ťδݤ��������ư����Τ�����ޤ������Τ褦�ʥ������Ǥϡ������ǤϤʤ����르�ꥺ�ब��ɽ�ɤ����ư��뤫�ɤ������ڤ��뤿��ˡ���֤Τ�������Ťδݤ�Ԥ��ޤ������Τ��Ȥ��������뤿�ᡢ���� 7 ���ѹ���˾������ޤ���
���� 7'
- m �� n �� IEEE 754 �����٤�ɽ����ǽ�� |m| < 252 �������ǡ�n �� n = 2i + 2j �Ȥ����ü�ʼ���ɽ������硢ξ������ư�������黻�������٤��������ݤ���뤫�����뤤�Ͻ��˳�ĥ�����٤˴ݤ����³���������٤˴ݤ����Ȥ���
(mn)
n = m �Ǥ��롣
����
»���ʤ��� m > 0 �Ȳ��ꤷ�ޤ���q = m
n �Ȥ��ޤ���2 ���߾�ǥ������뤷��
252 �� m < 253��252 �� q < 253 �Ȥʤ�Ʊ���������ͤ��뤳�Ȥ��Ǥ��ޤ������ξ�硢m �� q ��ξ���Ȥ⡢�Dz��̥ӥåȤ���˥åȤη���������� (�Ĥޤ�
ulp(m) = ulp(q) = 1) �Ǥ��������������� m < 252 �Ȳ��ꤷ�����ᡢ��������� m �϶����������Ǥ����ޤ���m �� q �Υ����������ͤ� m/2 < q < 2m �����������ᡢ�б����� n ���ͤϡ�m �� q �Τɤ��餬�礭�����˴�Ť��Ƽ��� 2 �Ĥμ��Τ����줫�ˤʤ�ޤ���
q < m �ξ�硢���餫�� 1 < n < 2 �Ǥ��ꡢn �� 2 �Ĥ� 2 ���߾��ͤι�פǤ��뤿�ᡢ����� k �ˤĤ��Ƥ� n = 1 + 2-k �Ǥ���Ʊ�ͤˡ�q > m �ξ�� 1/2 < n < 1 �Ǥ��뤿�ᡢn = 1/2 + 2-(k + 1) �Ǥ� (n �� 2 �Ĥ� 2 ���߾��ͤι�פǤ��뤿�ᡢ1 �ˤ�äȤ�ᤤ�ͤǤ��� n �� n = 1 + 2-52��m/(1 + 2-52) �ϡ�m ��꾮���� 2 ���ܤ˾������������ͤ����礭���ʤ����ᡢq = m �ȤϤʤ�ޤ���)��q ����뤿��δݤ������ e �Ȳ��ꤷ��q = m/n + e�������줿�� q
n �� m + ne �� 1 �٤ޤ��� 2 �ٴݤ�ͤǤ���Ȥ��ޤ����ǽ�ˡ����줾�����ư�������黻�������٤��������ݤ�������ͤ��Ƥߤޤ������ξ�硢|e| < 1/2 �Ǥ���n �μ���
1/2 + 2-(k + 1) �ξ�硢ne = nq - m �� 2-(k + 1) �������ܤǡ�|ne| < 1/4 + 2-(k + 2) �Ǥ�������ϡ�|ne| �� 1/4 ���̣���ޤ���m �ȼ����礭��ɽ����ǽ�ʿ��ͤκ��� 1 �Ǥ��ꡢm �ȼ��˾�����ɽ����ǽ�ʿ��ͤκ��� m > 252 �ξ�� 1��m = 252 �ξ�� 1/2 �Ǥ��뤳�Ȥ�פ��Ф��Ƥ������������Τ��ᡢ|ne| �� 1/4 �ξ�硢m + ne �� m �˴ݤ���ޤ� (m = 252 �� ne = -1/4 �ξ��Ǥ⡢�Ѥ� ��������˴ݤ�뵬§�ˤ�ä� m �˴ݤ���ޤ�)��Ʊ�ͤˡ�n �μ��� 1 + 2-k �ξ�硢ne �� 2-k �������ܤǡ�|ne| < 1/2 + 2-(k + 1) �Ǥ�������ϡ�|ne| �� 1/2 ���̣���ޤ���m �� q ����μ¤��礭�����ᡢ���ξ�� m = 252 �ˤϤʤ�ޤ����Τ��ᡢm �����ܤ���ɽ����ǽ�ʿ��ͤȤκ��� �� 1 �Ǥ����������äơ�|ne| �� 1/2 �ξ��� m + ne �� m �˴ݤ���ޤ� (|ne| = 1/2 �ξ��Ǥ⡢m �������Ǥ��뤿�� ��������˴ݤ�뵬§�ˤ�ä��Ѥ� m �˴ݤ���ޤ�)�����Τ˴ݤ����黻�ξ����ϰʾ�Ǥ�����Ťδݤ��Ԥ��黻�Ǥ� (�ºݤ� 2 �ٴݤ��줿���Ǥ�) q �����Τ˴ݤ��줿���Ȥʤ뤳�Ȥ����뤿�ᡢ�嵭��Ʊ���� |e| < 1/2 �Ǥ������ξ�硢q
n �� 2 �ٴݤ����Ȥ������¤��θ����ʤ�С��嵭��������ڤ����ѤǤ��ޤ������Τ��Ȥ��������뤿�ᡢ��ĥ�����ٷ����Ͼ��ʤ��Ȥ� 64 �Ĥ�ͭ���ӥåȤ���Ĥ��Ȥ� IEEE ���ʤ����ꤷ�Ƥ��ꡢ���Τ��� m �� 1/2 �� m �� 1/4 �ϳ�ĥ�����٤����Τ�ɽ����ǽ�Ǥ��뤳�Ȥ����դ��Ƥ����������������äơ�n �μ��� 1/2 + 2-(k + 1) �Ǥ��ꡢ���Τ��� |ne| �� 1/4 �Ǥ������ m + ne ���ĥ�����٤˴ݤ��ȡ�m �Ⱥ��� 1/4 �κ��������̤���������ޤ����嵭�˽Ҥ٤��褦�ˡ������ͤ������٤Ǥ� m �˴ݤ���ޤ���Ʊ�ͤˡ�n �μ��� 1 + 2-k �Ǥ��ꡢ���Τ��� |ne| �� 1/2 �Ǥ������ m + ne ���ĥ�����٤˴ݤ��ȡ�m �Ⱥ��� 1/2 �κ��������̤��������졢�����ͤ������٤Ǥ� m �˴ݤ���ޤ� (���ξ�� m > 252 �Ǥ��뤳�Ȥ����դ��Ƥ�������)��
�Ǹ�ˡ���Ťδݤ�Τ���� q ���������ݤ��줿���ǤϤʤ�����ͤ��Ƥߤޤ��礦�����ξ�硢�ǰ��ξ��ˤ� |e| < 1/2 + 2-(d + 1) �Ȥʤ�ޤ������ξ�硢d �ϳ�ĥ�����ٷ����ˤ�����;ʬ�ʥӥåȤο��Ǥ� (��¸�γ�ĥ�١��������ƥ�Ϥ��٤ơ����礦�� 64 �Ĥ�ͭ���ӥåȤˤ���ĥ�����ٷ����ݡ��Ȥ��Ƥ��ޤ������η����Ǥϡ�
d = 64 - 53 = 11)����Ťδݤ�ϡ���������˴ݤ�뵬§�ˤ�ä� 2 ���ܤδݤ���ꤵ�����˸¤������Τʴݤ��̤�Ф����ᡢq �϶����������Ǥʤ���Фʤ�ޤ��������äơ�n �μ��� 1/2 + 2-(k + 1) �ξ�硢ne = nq - m �� 2-k �������ܤǡ�
|ne| < (1/2 + 2-(k + 1))(1/2 + 2-(d + 1)) = 1/4 + 2-(k + 2) + 2-(d + 2) + 2-(k + d + 2) �Ǥ���k �� d �ξ�硢|ne| �� 1/4 �Ȥʤ�ޤ���k > d �ξ�硢|ne| �� 1/4 + 2-(d + 2) �Ǥ����ɤ���ξ��⡢�Ѥκǽ�δݤ�ˤ�� m �Ⱥ��� 1/4 �κ��������̤����դ��졢���������ڤ˽��ä� 2 ���ܤδݤ�ˤ�� m �˴ݤ���ޤ���Ʊ�ͤˡ�n �μ��� 1 + 2-k �ξ�硢ne ��
2-(k - 1) �������ܤǡ�|ne| < 1/2 + 2-(k + 1) + 2-(d + 1) + 2-(k + d + 1) �Ǥ���k �� d �ξ�硢|ne| �� 1/2 �Ǥ���k > d �ξ�硢|ne| �� 1/2 + 2-(d + 1) �Ǥ����ɤ���ξ��⡢�Ѥκǽ�δݤ�ˤ�� m �Ⱥ��� 1/2 �κ��������̤����դ��졢�����ξ����˽��ä� 2 ���ܤδݤ�ˤ�� m �˴ݤ���ޤ����������ξ����ϡ�������Ťδݤ��������������ˤΤ��Ѥ���Ťδݤ����������������ξ��Ǥ���������̤˴ݤ�뤳�Ȥ��Ƥ��ޤ��������ξ����Ϥޤ�����������Ťδݤ�β�ǽ����ޤ��Ȥ����ޤdz�ĥ���뤳�Ȥϡ����ä� 2 �Ĥ���ư�������黻�����ޤޤʤ��ץ������Ǥ⺤��Ǥ��뤳�Ȥ⼨���Ƥ��ޤ�����ä�ʣ���ʥץ������Ǥϡ���Ťδݤ�θ��̤��η�Ū���������뤳�Ȥ��̾��Բ�ǽ�Ǥ��������ٱ黻�ȳ�ĥ�����ٱ黻�ΰ���Ū���Ȥ߹�碌�ϸ����ޤǤ⤢��ޤ���
��ĥ���٤��Ф���ץ�����ߥ��쥵�ݡ���
��������ϡ���ĥ���� per se ��ͭ���Ǥ���ȽҤ٤Ƥ���ΤǤϤ���ޤ��ץ�����ޤ���ĥ���٤����ƻ��ѤǤ�����ˤϡ�¿���Υץ�����ब��ĥ���٤β��ä����뤳�Ȥ��Ǥ��ޤ�����ǰ�ʤ��顢���ߤΥץ�����ߥ���ϳ�ĥ���٤ĤɤΤ褦����ˡ�ǻ��Ѥ���٤����ץ�����ޤ����ꤹ�뤿��ν�ʬ�ʼ��ʤ����Ƥ��ޤ��ɤΤ褦�ʥ��ݡ��Ȥ�ɬ�פ������ᡢ�����Ǥϳ�ĥ���٤λ��Ѥ����椹����ˡ��Ƥ���ޤ���
̾�ܾ�κ�����٤Ȥ��������٤���Ѥ���ܿ����Τ���ץ������Ǥϡ���깭�����٤λ��Ѥ����椹����ˡ�Ȥ��Ƽ��� 5 �Ĥ����ѤǤ��ޤ���
- ��ĥ�١����Υ����ƥ�Ǥϡ���ǽ�ʤ������ĥ���٤���Ѥ��Ƥ�äȤ�®�������ɤ���������褦�˥���ѥ��뤹�롣�ۤȤ�ɤο��ͥ��եȥ������Ǥϡ��֥ޥ��ץ�����פ��ϰ����ꤹ��Ʊ黻�����и����ʾ�α黻��ɬ�פȤ��ޤ������Υǡ����������٤dz�Ǽ������硢�������٤ˤ������������дݤ�����Ȥ����̾�ޥ��ץ������Ѥ���ޤ������Τ��ᡢ���ϥǡ��������ϻ��˴ݤ�ʤ��줿�� (�������ޤ��ϸ��ä�) ���ꤵ�졢��̤Ϥ���餬��Ǽ�����Ȥ���Ʊ�ͤ˴ݤ���ޤ����������äơ���ĥ���٤Ǥ���ַ�̤η��Ϥ�����Τʷ�̤�����������⤢��ޤ�������ĥ���٤�ɬ�ܤǤϤ���ޤ����ξ�硢���Τ����ۤɥץ�������®�٤��㲼���ʤ��Ȥ���������ѥ���dz�ĥ���٤���Ѥ�������ʳ��Ǥ������٤���Ѥ��뤳�Ȥ��ᤷ�ޤ���
- Ŭ�٤˹�®�ǽ�ʬ�������������٤������������Ѥ�������ʳ��ǤϤۤ��η�������Ѥ��롣������ˤϡ���ĥ���٤����ѤǤ���Ф�äȴ�ñ�˼¹ԤǤ����Τ�����ޤ��������������Τ褦�ʷ��⤤���餫;ʬ�ʼ�֤�������ǡ������٤Ǥ�¹ԤǤ��ޤ����������ͤΥ٥��ȥ�Υ桼����å�������������뤳�Ȥ����ꤷ�ޤ������Ǥ���������������ؿ��ϰϤ���Ѥ��� IEEE 754 ��ĥ�����ٷ����Ǥ����ι�פ����Ѥ��뤳�Ȥˤ�ꡢ�ºݤ�Ĺ���Υ٥��ȥ���Ф�����ޤä���������ե����ޤ��ϥ����С��ե�����������ˡ���ɤ����Ȥ��Ǥ��ޤ�����ĥ�١��������ƥ�Ǥϡ����줬��������������äȤ�®����ˡ�Ǥ���
ñ���� / �����٥����ƥ�Ǥϡ���ĥ�����ٷ����ϥ��եȥ�������ǥ��ߥ�졼�Ȥ���ɬ�פ����� (��ĥ�����ٷ��������ݡ��Ȥ���Ƥ�����)����������ե����ޤ��ϥ����С��ե�����ȯ�����Ƥ��ʤ�����ǧ���뤿����㳰�ե饰��ƥ��Ȥ����⤷ȯ�����Ƥ�����ˤ�����Ū�ʥ�������ˤ������֤�����ˡ����Τ褦�ʥ��ߥ�졼������ñ��������٤���Ѥ������������®�٤��㲼���ޤ�����ĥ���٤Τ��Τ褦�ʻ��Ѥݡ��Ȥ��뤿��ˡ�����ϡ����Ѥ����åɤ�ץ�����ब����Ǥ���褦�ˡ�Ŭ�٤˹�®�����ѤǤ�����Ǥ�äȤ���������ȤȤ�ˡ����η�������ʬ�������� (���Ȥ��������٤�����ϰϤǤ��뤳��) ��ץ�����ब���ڤǤ���褦�ˤ��줾��η��������٤��ϰϤ��Ķ��ѥ���������ɬ�פ�����ޤ���- ���եȥ������ǥ��ߥ�졼�Ȥ���ɬ�פ�������Ǥ⡢�����٤�깭����������Ѥ��롣�桼����å��������������ʣ���ʥץ������Ǥϡ��ץ�����ޤ� 2 ����Υץ������Ҥ���ɬ�פ��������®�٤��٤��Ƥ��ĥ���٤���뤳�Ȥ�˾���礬����ޤ������ξ������ϡ����ѤǤ�����ǺǤ��ϰϤι����������ϰϤ����٤�ץ�����ब��ǧ�Ǥ���褦�ˡ��Ķ��ѥ���������ɬ�פ�����ޤ���
- �����٤�깭�����٤���Ѥ��ʤ� (�ϰϤ���ĥ������礬���뤬�������ٷ��������٤��������ݤ����)���嵭���������Ƥ��뤤���Ĥ�����Τ褦�ˡ��������ݤ���������ٱ黻�˰�¸����褦�ˤ����äƴ�ñ�˵��Ҥ����ץ������ξ�硢��ַ�̤������٤�����ؿ��ϰϤΥ쥸�����Ƿ��Ǥ���Ȥ��Ƥ⡢����ϳ�ĥ���٤����Ѥ���ʤ��褦�˻ؼ�������ˡ��ץ�����ޤ�����ɬ�פ�����ޤ���������ˡ�Ƿ��������ַ�̤Ǥ⡢����˳�Ǽ�����Ȥ��˥�������ե������������Ťδݤ������������ޤ������ѱ黻�η�̤����� 53 �Ĥ�ͭ���ӥåȤ˴ݤ��졢�������������ɬ�פ�����Ȥ��˰���³���Ƥ�꾯�ʤ�ͭ���ӥåȤ˺ƤӴݤ����褦�ʾ�硢�ǽ���̤������������� 1 �٤����ݤ����˼������줿��̤Ȥϰۤʤ��礬����ޤ�����������Τ褦����Ťδݤ�ºݤΥץ������������ʱƶ���Ϳ�����ǽ���ϤۤȤ�ɤ���ޤ���
- �����ٷ��������٤��ϰϤ�ξ�����������ݤ���롣�����٤Τ��Τ��Ӥ��������ϡ������ٷ������ϰϤ����٤�ξ���θ��ٶ�ǡ����ͥ��եȥ������ޤ��ϱ黻���Τ�Τ�ƥ��Ȥ���ץ������˺Ǥ������Ǥ������Τ褦�����տ����ƥ��ȥץ������ϡ��ܿ���ǽ����ˡ�ǵ��Ҥ���Τ��̾ﺤ��Ǥ��ꡢ����η����˷�̤���Ū�˴ݤ�뤿��˥��ߡ��Υ��֥롼�����ۤ��Υȥ�å�����Ѥ��ʤ���Фʤ�ʤ����ˤϤ�����������顼�������䤹���ʤ�ޤ����������äơ���ĥ�١��������ƥ����Ѥ��Ƥ����� IEEE 754 �����˰ܿ���ǽ�ʶ��Ǥʥ��եȥ�������ȯ����ץ�����ޤϡ��³��줿ϫ�Ϥ��뤳�Ȥʤ�ñ���� / �����٥����ƥ�α黻�ߥ�졼�ȤǤ��뤳�Ȥο�������ǧ���褦�ˤʤ�Ǥ��礦��
������ 5 �ĤΥ��ץ����٤ƥ��ݡ��Ȥ���褦�ʸ���ϸ��ߤ���ޤ��ºݡ���ĥ���٤λ��Ѥ�����Ǥ��뵡ǽ��ץ�����ޤ���������ϤۤȤ�ɤ���ޤ��������㳰�� 1 �Ĥϡ�����ɸ�ಽ�κǽ��ʳ��ˤ��� C ����κǿ���ӥ����ISO/IEC 98 99; 1999 �ץ�����ߥ���Ǥ��� C ɸ�� �Ǥ���
���ߤ� C ɸ���Ʊ�͡�C99 ɸ�� �ϡ��̾��Ϣ�դ����Ƥ������������Ǽ���ɾ�������������Ĥ��Ƥ��ޤ��������� C99 ɸ��ϡ�����ɾ������ 3 �Ĥ���ˡ�Τ����ɤ줫 1 �Ĥ���Ѥ��뤳�Ȥ�侩���Ƥ��ޤ����侩����Ƥ��뤳�� 3 �Ĥ���ˡ�ζ��̤ϡ�������깭�������ˡֳ�ĥ�פ���뤽�����٤ˤ���ޤ���C99 ɸ��ϡ��ץ�ץ����å��ޥ���
FLT_EVAL_METHOD��������뤳�Ȥˤ����Ѥ����åɤ���������̤��뤳�Ȥ�侩���Ƥ��ޤ���FLT_EVAL_METHOD�� 0 �ξ�硢���줾��μ��Ϥ��μ�����б����������ɾ������ޤ���FLT_EVAL_METHOD�� 1 �ξ��ϡ�float�μ���double���б���������˳�ĥ����ޤ���FLT_EVAL_METHOD�� 2 �ξ��ϡ�float��double��long double���б���������˳�ĥ����ޤ� (����ɾ����ˡ�������Բ�ǽ�Ǥ��뤳�Ȥ����ᡢFLT_EVAL_METHOD�� -1 �����ꤹ�뤳�Ȥ������˵��Ĥ���Ƥ��ޤ�)��C99 ɸ��ϡ�<math.h>�إå����ե����뤬��float_t��double_t��������뤳�Ȥ�ꤷ�Ƥ��ޤ���float_t�Ͼ��ʤ��Ȥ�float��Ʊ�������Ǥ��ꡢdouble_t�Ͼ��ʤ��Ȥ�double��Ʊ�������Ǥ��������ϡ�float�����double�μ���ɾ���˻��Ѥ��뷿���̾���פ��ޤ������Ȥ��С�FLT_EVAL_METHOD�� 2 �ξ�硢float_t��double_t�Ϥɤ����long double�Ǥ���C99 ɸ��ϡ�<float.h>�إå����ե����뤬�����줾�����ư�������η����б�����������ϰϤ����٤���ꤹ��ץ�ץ����å��ޥ�����������뤳�Ȥ��ꤷ�Ƥ��ޤ���C99 ɸ�ब����ޤ��Ͽ侩���뵡ǽ���Ȥ߹�碌��ȡ��嵭�˼����� 5 �ĤΥ��ץ����ΰ��������ݡ��Ȥ���ޤ������Ȥ��С�������
long double�����ĥ�����ٷ����˳�����ơ�FLT_EVAL_METHOD�� 2 ����������硢�ץ�����ޤϳ�ĥ���٤����Ū��®�Ǥ��ꡢ���Τ���桼����å���������Τ褦�ʥץ������Ϸ�long double(�ޤ���double_t) ������ѿ�����ѤǤ��������Ǥ��ޤ�������������Ʊ�������ϡ�̵̾�μ����ĥ���٤��ݻ�����ɬ�פ�����ޤ�������ϡ�����餬����˳�Ǽ������� (����ѥ��餬��ư�������쥸�����դ줵����ɬ�פ�������ʤ�) �Ǥ�Ʊ�ͤǤ����ޤ���double��������줿�ѿ��˳�����Ƥ�줿���η�̤��Ǽ���������������٤��Ѵ�����ɬ�פ�����ޤ�������ϡ����η�̤�쥸�������ݻ��Ǥ������Ǥ�Ʊ�ͤǤ����������äơ�double����double_t���Ȥ⡢���ߤγ�ĥ�١����ϡ��ɥ������ǤϺǤ�®�������ɤ���������褦�ˤϥ���ѥ���Ǥ��ޤ�����������㤬�����Ƥ������ (���٤ƤǤϤʤ�) ������ϡ�C99 ɸ�ब������ʤDz��Ǥ��ޤ�����
1.0 + x��Ǥ�դη����ѿ����������졢�����ѿ�����˻��Ѥ�����硢log1p�ؿ��� C99 ɸ��С�������������ư��뤳�Ȥ��ݾڤ���Ƥ��ޤ����������������ٿ����̤Ȳ��̤���ʬ��ʬ�䤹�뤿��ΰܿ����Τ����ΨŪ�� C99 ɸ��ץ������ϡ����Ū����Ǥ���double�μ��������٤��������ݤ���뤳�Ȥ��ݾڤǤ��ʤ���硢�ɤ���������Τʰ��֤�ʬ�䤷����Ťδݤ���뤳�Ȥ��Ǥ���Ǥ��礦����1 �Ĥβ��ˡ�Ȥ��ơ�double_t������Ѥ���С�ñ���� / �����٥����ƥ�Ǥ������٤�ʬ�䤷����ĥ�١��������ƥ�Ǥϳ�ĥ���٤�ʬ��Ǥ��ޤ�������ǡ��ɤ���ξ���黻���������ݤ���ޤ������� 14 �ϡ����äȤʤ�黻�����٤��狼��ФɤΥӥåȰ��֤ˤ����Ƥ�ʬ�䤬��ǽ�Ǥ���Ȥ��Ƥ��ޤ������ξ���ϡ�FLT_EVAL_METHOD�ȴĶ��ѥ����ޥ����Ǽ����Ǥ��ޤ������Υե饰���Ȥϡ���ǽ�ʼ�������Ƥ��ޤ���
�������Υ���塼�����Ĥ���ˤϡ��ץ�����ޤϡ�
double�μ��ϳ�ĥ���٤�ɾ������뤳�Ȥ����뤳�ȡ���Ťδݤ�����꤬��³����ȥ��르�ꥺ��θ�ư���������������Ȥ����뤳�ȡ���������� 14 �˽��äƳ�ĥ���٤����ѤǤ��뤳�Ȥ�ǧ������ɬ�פ�����ޤ�����ä����Ƥʥ���塼�����Ȥ��ơ����줾��μ��������٤��������ݤ����褦�˻��ꤹ�뤳�Ȥ�Ǥ��ޤ�����ĥ�١��������ƥ�Ǥϴݤ����٥⡼�ɤ��ѹ�����Ф��ߤޤ�������ǰ�ʤ��� C99 ɸ�� �Ϥ����»ܤ���������Τ�����ˡ�����Ƥ��ޤ�����ư�������ݡ��Ȥ��뤿��� C ɸ��˲ä����ѹ�����ꤷ�����ʸ��Floating-Point C Edit �ν������Ƥϡ��ݤ����٥⡼�ɤ������������ƥ�ˤ���������ǡ��ݤ����٤μ����������Ԥ�fegetprec�����fesetprec�ؿ� (�ݤ������μ����������Ԥ�fegetround�����fesetround�ؿ�������������) �����뤳�Ȥ�侩���Ƥ��ޤ��������ο侩�ϡ�C99 ɸ����Ƥ��ѹ����ä��������˽�����ޤ������ޤ����ۤʤ������黻��ǽ����ijƼ�Υ����ƥ�֤ΰܿ����ݡ��Ȥ���C99 ɸ��Υ��ץ������ϡ��ۤʤ���ư�������������ƥ�����ݡ��Ȥ�����ͥ�줿��ˡ�����Ƥ��ޤ������줾��� C99 ɸ������ϡ����μ��������ݡ��Ȥ������������������
<inttypes.h>�إå����ե�����뤷�Ƥ��ޤ���������������̾���ϡ������Υ������ȸ�Ψ�˽��ä��դ����Ƥ��ޤ������Ȥ��С�int32_t�Ϥ��礦�� 32 �ӥåȤ�������������int_fast16_t�Ϥ��μ����ǺǤ�®������ 16 �ӥå�������������intmax_t�ϥ��ݡ��Ȥ���Ƥ�����ǺǤ���������Ǥ�����ư�������η��ˤĤ��Ƥ⡢��������ηϤ������Ǥ��ޤ������Ȥ��С�float53_t�Ϥ��礦�� 53 �ӥåȤ����٤Ǥ��뤬�ϰϤ������Ķ���뤳�Ȥ⤢����ư��������float_fast24_t�����٤����� 24 �ӥåȤǤ��뤽�μ����κǤ��®�ʷ���floatmax_t�ϥ��ݡ��Ȥ���Ƥ�����ǺǤ��Ŭ�٤˹�®�ʷ���̾���Ȥ��ƻ��ѤǤ��ޤ�����®�ʷ�����Ѥ���ȡ��쥸���������դ줿��̤Ȥ���̾���դ��ѿ����ͤ��ѹ�����ƤϤʤ�ʤ��Ȥ������¤�����ޤ�������ĥ�١��������ƥ��Υ���ѥ���ϲ�ǽ�ʤ�����Ǥ�®�������ɤ������Ǥ��ޤ����������礦�ɤη������Ѥ����ȳ�ĥ�١��������ƥ�Υ���ѥ���ϡ��嵭��Ʊ�����¤���Ȥ��ơ��ݤ����٥⡼�ɤ����ꤵ�줿���٤˴ݤ��褦�����ꤷ����깭���ϰϤ���Ĥ��ޤ���double_t�ϡ����Τ�������ɾ������ˡ�IEEE 754 �������ٷ��������٤��ϰϤ�ξ������ķ���̾���Ȥ��ƻ��ѤǤ��ޤ������Τ褦���ηϤ���٤�̾�����դ����Ķ��ѥ����ޥ����ȤȤ�˻��Ѥ���ȡ����Ҥ��� 5 �ĤΥ��ץ������ñ�˥��ݡ��ȤǤ����ץ�����ޤϥץ�����बɬ�פȤ�����ư��������̣�����ñ�ˤ�������ʷ��ǻ���Ǥ��ޤ�����ĥ���٤θ��쥵�ݡ��ȤϤ���ۤ�ʣ���ʤΤǤ��礦����ñ���� / �����٥����ƥ�Ǥϡ��嵭�� 5 �ĤΥ��ץ������ 4 �Ĥ����ƤϤޤꡢ��®�ʷ������Τ��ϰϤη�����̤���ɬ�פϤ���ޤ���������ĥ�١��������ƥ�Ǥϡ�������ˤ��ޤ��ޤ�����ĥ�١��������ƥ�ϡ����������ٱ黻�����ʳ�ĥ���ٱ黻�Τɤ���⡢�������Ȥ߹�碌�ξ���Ʊ����Ψ�Ǥϥ��ݡ��Ȥ������ץ������ˤ�äưۤʤ��Ȥ߹�碌���ᤷ�ޤ����ޤ������ij�ĥ���٤���Ѥ��뤫�Ȥ�������ϡ���ư�������黻�ϡ����������ΡפǤ��ꡢ�������ä������黻�ˤդ��路���ʤ�������ͽ¬�Ϥ�ʤ��ȥ٥���ޡ������鸫�ʤ����������� (���ˤϿ��ͥ��ʥꥹ�Ȥˤ�äƤ��Τ褦�˸����ȸ���뤳�Ȥ⤢��ޤ�) ����ѥ���饤������Ǥ���ƤϤʤ�ޤ���������ϥץ�����ޤˤ���ͤ�٤��Ǥ����ץ�����ޤϡ����������ʬɽ���Ǥ�������ɬ�פȤ��ޤ���
����
���Ҥ���ɾ�ϡ���ĥ�١��������ƥ�����뤳�Ȥ��ͤ餤�ǤϤʤ������ΰտޤϤ����Ĥ��θ��ä����� (���κǤ����Τϡ����٤Ƥ� IEEE 754 �����ƥ��Ʊ��ץ��������Ф��ޤä���Ʊ����̤�Ф��ʤ���Фʤ�ʤ��Ȥ������) �����餫�ˤ��뤳�Ȥˤ���ޤ�������ޤdz�ĥ�١��������ƥ��ñ���� / �����٥����ƥ�֤ΰ㤤�˾��������ƤƤ��ޤ����������줾��Υ��롼�פˤ�����Ƽ�Υ����ƥ�֤ˤϤ������㤬����ޤ������Ȥ��С�ñ���� / �����٥����ƥ����ˤϡ�2 �Ĥο���ݤ��� 3 �Ĥ�ο�����ñ���̿��ǡ��Ǹ�� 1 �Ĥδݤᤷ���Ԥ�ʤ���Τ�����ޤ������軻/�û��κ���黻�פȸƤФ�뤳�α黻�Ǥϡ��ץ�������ñ���� / �����٥����ƥऴ�Ȥ˰ۤʤ��̤��������ޤ������α黻�Ǥϡ���ĥ���٤Τ褦�ˡ��ץ�����ब���Ѥ���뤫�ɤ����������Ƥ��Ļ��Ѥ���뤫�ˤ�äơ�Ʊ�������ƥ��Ǥ�Ʊ���ץ�����ब�ۤʤ��̤�����������⤢��ޤ� (�־軻/�û��κ���黻�פϡ�ʬ�䤻����¿�����٤ξ軻��¹Ԥ��뤿��������Ū����ˡ�ǻ��ѤǤ��ޤ��������� 6 ��ʬ��ץ������ɤ���ˤʤ�ʤ���礬����ޤ�)��IEEE ���ʤ����ˤ��Τ褦�ʱ黻��ͽ�ۤ��ʤ��ä��Ȥ��Ƥ⡢��֤��Ѥϥ桼�������椬�ڤФʤ����Τ��ݻ���������ι�������ä��ְ���פ����ۤ��졢�ǽ��ι�פϤ���ñ���٤ޤ��������٤ΰ���Υ������˹礦�褦���������ݤ���ޤ���
IEEE 754 �ϰ���Υץ�����ब���ۤ��٤���̤����Τ˵��ꤷ�Ƥ���Ȥ����ͤ��ϡ���Ϥ�̥��Ū�Ǥ���¿���Υץ�����ޤϡ��ץ�������ѥ��뤹�륳��ѥ����ץ�������¹Ԥ��륳��ԥ塼���ˤ������ʤ��ץ�������ư�������Ǥ����ץ�����ब������ư��뤳�Ȥ�����Ǥ���ȿ���������ޤ������γο��ݡ��Ȥ��뤳�Ȥϡ�����ԥ塼�������ƥ��ץ�����ߥ�����߷ԤˤȤä��礤�˲��ͤΤ�����ɸ�Ǥ�����ǰ�ʤ��顢��ư�������黻�˴ؤ��Ƥϡ�������ɸ�ϼºݡ�ã�����Բ�ǽ�Ǥ���IEEE ���ʤμ�ɮ�ԤϤ����ǧ�����Ƥ��ꡢ����ã�����ߤƤϤ��ޤ����η�̡�����ԥ塼���ȳ��Τۤ����Τ��ۤȤ�ɤ� IEEE 754 ɸ��˽�Ƥ���ˤ⤫����餺���ܿ����Τ��륽�եȥ������γ�ȯ���ݤ���ץ�����ޤϡ�ͽ¬�Բ�ǽ����ư�������黻�˼���Ȥ�³���ʤ���Фʤ�ޤ���
�ץ�����ޤ� IEEE 754 ����ħ�����Ѥ���ΤǤ���С���ư�������黻��ͽ�۲�ǽ�ʤ�ΤˤǤ���ץ�����ߥ��줬ɬ�פǤ���C99 ɸ��Ǥϡ�
1 ����ʳ���ɽ���Ȥ��ơ���ư����������å��塢���������դ��п�������ޤ� (Matula/Kornerup 1985��Swartzlander/Alexopoulos 1975 )�� 2 �����Ѹ�ϡ�Forsythe/Moler �� 1967 ǯ������ޤǤβ������֤������ɽ���Ȥ��ƺ��Ѥ�����ΤǤ��� 3 �����Ǥϡ��ؿ���ͭ�շ�ξ�̤˳�Ǽ���뤳�Ȥ�����Ȥ��ޤ��� 4 z ���ͤ� ��emax+1 ��Ķ���ʤ���硢���뤤�� ��emin �������ʤ���������ޤ��������ϰϤ�Ķ������ˤĤ��Ƥϡ������Ǥϰ����ޤ��� 5 z' �ϡ�z �˶��������ư���������Ȥ��ޤ���|d.d...d - (z/��e) |��p-1 �� |z'-z|/ulp(z') ���������ʤ�ޤ� ��������¬�ꤹ�뤵������Τʸ����� |z'-z|/ulp(z) �Ǥ���--Ed 6 70 �ǤϤʤ� 700 �Ǥ���0.1 - 0.0292 = 0.0708 �ʤΤǡ�ulp (0.0292 ) �θ����� 708 ulp �Ȥʤ�ޤ���- Ed 7 (x - y)(x + y) �μ��Ǥϰ������껦�ϵ����ʤ���Τ�FLT_EVAL_METHOD���Ȥ˥ץ�������ʣ���������ʤ���Фʤ�ޤ�����ʬͽ¬�������夷�Ƥ��ޤ�������θ���Ǥ� IEEE 754 ��̣���˰�¸�����ϰϤ�����˼�����ʸ�ˤ�ꡢñ��Υץ������Ҥ���Ф��फ�ɤ����Ϥޤ����餫�ǤϤ���ޤ���¸�γ�ĥ�١��������ƥ�ϡ��黻������Υ����ƥ�ǤɤΤ褦�˹Ԥ���٤����ϥץ�����ޤ��⥳��ѥ���ȥϡ��ɥ������������褯ǧ���Ǥ���Ȼ䤿���˷����ޤ��뤳�Ȥˤ�ꡢ���θ��̤������Ƥ��ޤ������η����ߤ� 2 ���ܤθ����Ǥ�������̤˵����������٤ϡ���̤���������ޥ���ǤϤʤ�����̤�������Ф��������ˤ�äƤΤ߷�ޤ�ޤ��������η������������İ��Ǥ���Τϡ��ץ�����ޡ�����ѥ��顢�ϡ��ɥ������Τ������������ץ�����ޤ����Ǥ����ޤ���
�ξ��� x2 - y2 ����鷺�������٤�����ޤ������ξ�硢x2 - y2 �ξ��������������Ȥ��˵�����ݤ���������ǽ�Ū�ʸ����˱ƶ���Ϳ���뤳�ȤϤʤ��Τǡ� (x - y)(x + y) �δݤ������ 3���ޤ� x2 - y2 �δݤ������ 2 �ˤʤ�ޤ��� 8 �����Τʴݤ����פϱ�ʸ�Ǹ��� "exactly rounded operation" �ޤ��� "correctly rounded operation" �Τ��ȤǤ��� 9 n = 845 �ξ��m��xn = 9.45��xn + 0.555 = 10.0��10,0 - 0.555 = 9.45 �Ȥʤ�ޤ����������äơ�n > 845 �ˤĤ��Ƥ� xn = x845 �Ȥʤ�ޤ��� 10 �ʿ��ξ�硢q ��
������������ޤ���-Ed 11 2 �ʳ��δ���ˤĤ��Ƥ��ɼԼ��Ȥdz�ǧ���ƤߤƤ���������- Ed 12 ����ϡ�Knuth (1981��211�ڡ���) �ˤ��� Konrad Zuse �˹ͰƤ��줿�Ȥ���Ƥ��ޤ�����Goldberg (1967) �ˤ�äƺǽ��ȯɽ���줿�褦�Ǥ��� 13 Kahan �ˤ��ȡ���ĥ���٤ˤ� 64 �ӥåȤ�ͭ�շ夬���ݤ���ޤ�������ϡ�����������֤�夲���ˡ�Intel 8087 ��ǥ��������ŤǤ���Ǥ����������٤Ǥ��뤫��Ǥ��� 14 Kahan������� LeBlanc (1985 ) ����Ƥ������ܱ黻�� 1 �ĤȤ������Ѥ�ä��뤳�Ȥˤ�ȿ���⸫���ޤ��� 15 Kirchner �ϼ��Τ褦�˻�Ŧ���Ƥ��ޤ�����1 �����å����������뤢���� 1 �Ĥ���ʬ�Ѥ��ġ�1 ulp ����θ����ˤ��ϡ��ɥ�����������Ѥ�����뤳�Ȥ��Ǥ��롣��
16 CORDIC �Ȥϡ�"Coordinate Rotation Digital Computer"��Ƭ����ǡ�����ˤ�ꡢ�ۤȤ�ɤν��������եȤ�û��ǹ�������� (�軻��������ۤȤ�ɤʤ���) Ķ�۴ؿ�������뤳�Ȥ��Ǥ��ޤ� (Walther 1971)��CORDIC �ˤ�ꡢ�ϡ��ɥ��������ɲä������Ǥ�®�٤˱����ƾ軻�異�쥤����ӤǤ���褦�ˤʤ�ޤ���d �� Intel 8087 ��Motorola 68881 ��ξ���ǻ��Ѥ���ޤ���
17 ����ϡ���̯�����Ǥ���IEEE �黻�Υǥե���ȤǤϥ����С��ե������������˴ݤ���ޤ������ǥե���Ȥ��ѹ����뤳�Ȥ�Ǥ��ޤ� (�ִݤ�⡼�ɡ��Ȥ��Ƥ�������)�� 18 ����ϡ�854 �Ǥϥ��֥Ρ��ޥ롢754 �Ǥ��������ȸƤФ�ޤ��� 19 ���줬��ɸ�ಽ�κǤ�ʣ����¦�̤Ǥ������ˤ˥�������ե�������ץ������ϡ����եȥ������ȥ�åפ���Ѥ���ϡ��ɥ������Ǥ϶�ü�˥ѥե����ޥ��㲼���ޤ���
20 ���ˡ֥ȥ�åספ��� NaN ��ȼ��ʤ��¤ꡢ̵�������㳰�ϵ����ޤ��ܺ٤ˤĤ��Ƥϡ�IEEE Std 754-1985 �� 6.2 ��Ȥ��Ƥ���������-Ed 21 x�� y ��ξ������ξ�硢��
����礭���ʤ��礬����ޤ��� 22 x < 1, n < 0 �� x-n ������������ե����θ³� 2e min���鷺���˾��������ϡ�
�Ȥʤ�Τǡ�IEEE �����٤Ϥ��٤� -emin < emax �Ȥʤ뤳�Ȥˤ�ꡢ�����С��ե����ϵ����ޤ��� 23 ����Ϥ����餯���߷Ԥ���ư������̿������٤��ºݤ��������Ω����ľ�Դط���̿��åȤ����ȿ�Ǥ�����ΤǤ����軻�����̤ʥ�������ǧ��뤳�Ȥˤ�ꡢ����ľ�Դط����ʤ��ʤ�ޤ��� 24 �����Ǥϡ�3.0 ��ñ���٤������3.0D0 �������٤�����Ǥ��뤳�Ȥ�����Ȥ��ޤ��� 25 0 0 = 1 �Ȥ���Ƚ�Ǥϡ�f ��������Ǥ��뤳�Ȥ��ꤹ�����¤˰�¸���ޤ����������¤��ʤ���С�f ���դ� 0 �Ȥ��뤳�Ȥˤ�ꡢ�ؿ��ϡ�limx � 0f(x)g(x) ���ͤȤ��� 0 ���֤��ޤ����������äơ�0 0�� NaN ���������뤳�Ȥˤʤ�ޤ��� 26 0 0�ˤĤ��Ƥϡ����ޤ��ޤʵ�����;�Ϥ�����ޤ������Ǥ������ϤΤ��������� "Concrete Mathematics" (Graham��Knuth��Patashnik����) �ǡ��������������Ω�Ĥˤ� 0 0 = 1 �Ǥʤ���Фʤ�ʤ��Ȼ�Ŧ���Ƥ��ޤ���
27 �ݤ�⡼�ɤ� -�ؤδݤ�ˤʤäƤ�����Ͻ����ޤ� (���ξ��� x - x = -0 �Ǥ�)�� 28 VAX �� VMS ���إ饤�֥��Ǥϡ���®�� CALLS �� CALLG ̿�������ˡ��������륵�֥롼������ȤΤ�����ʤ������ǸƤӽФ��Ȥ�����̣�ǡ����Υ���饤�ץ����������ִ�����Ѥ��Ƥ��ޤ��� 29 ���ִ������ϡ��ϡ��ɥ������ˤ��ľ��Ū�ʼ�����ɬ�פˤʤ������ޤ����եȥ�������ǥ���ץ���Ȥ�����ϡ�Ϣ³Ū����ư�������Υȥ�åפ����ꤹ��Ȥ����ˤ���ޤ���- Ed 30 ����ά���ξ����Ǥϡ���= 2 ������Ȥ���Τǡ�4 �ˤ��軻�����Τ˹Ԥ��뤿�ᡢ��i ��ɬ�פ���ޤ��� 31 (bkx + wbk) �� bkx �η������ݻ��������˸¤ꡢ�ݤ�ˤ�ꡢbkx + wbk - rbk �Ȥʤ�ޤ���-Ed
|
���ޥ����������ƥॺ������� Copyright information. All rights reserved. |
�ۡ��� | �ܼ� | ���ڡ����� | ���ڡ����� | ���� |