2.3.4 Error Properties of Gradual Underflow

Most of the time, floating-point results are rounded:

computed result = true result + round-off

One convenient measure of how large the round-off can be is called a unit in the last place, abbreviated ulp. The least significant bit of the fraction of a floating-point number in its standard representation is its last place. The value represented by this bit (e.g., the absolute difference between the two numbers whose representations are identical except for this bit) is a unit in the last place of that number. If the computed result is obtained by rounding the true result to the nearest representable number, then clearly the round-off error is no larger than half a unit in the last place of the computed result. In other words, in IEEE arithmetic with rounding mode to nearest, it will be the computed result of the following:

0 ≤ |round-off| ≤½ulp

Note that an ulp is a relative quantity. An ulp of a very large number is itself very large, while an ulp of a tiny number is itself tiny. This relationship can be made explicit by expressing an ulp as a function: ulp(x) denotes a unit in the last place of the floating-point number x.

Moreover, an ulp of a floating-point number depends on the precision to which that number is represented. For example, Table 2–12 shows the values of ulp(1) in each of the four floating-point formats described above:

Table 2-12  ulp(1) in Four Different Precisions

Precision Value single ulp(1) = 2^-23 ~ 1.192093e-07 double ulp(1) = 2^-52 ~ 2.220446e-16 double extended (x86) ulp(1) = 2^-63 ~ 1.084202e-19 quadruple ulp(1) = 2^-112 ~ 1.925930e-34

Recall that only a finite set of numbers can be exactly represented in any computer arithmetic. As the magnitudes of numbers get smaller and approach zero, the gap between neighboring representable numbers narrows. Conversely, as the magnitude of numbers gets larger, the gap between neighboring representable numbers widens.

For example, imagine you are using a binary arithmetic that has only 3 bits of precision. Then, between any two powers of 2, there are 2³ = 8 representable numbers, as shown in the following figure.

Figure 2-6  Number Line

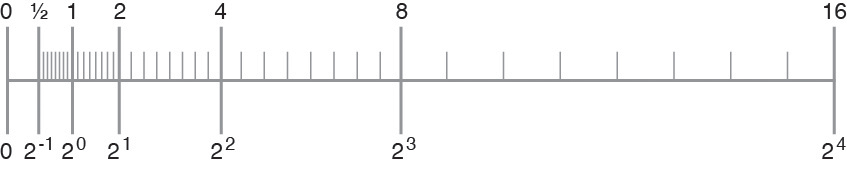
The number line shows how the gap between numbers doubles from one exponent to the next.

In the IEEE single format, the difference in magnitude between the two smallest positive subnormal numbers is approximately 10^{- 45}, whereas the difference in magnitude between the two largest finite numbers is approximately 10³¹!

In Table 2–13, nextafter(x,+∞) denotes the next representable number after x as you move along the number line towards +∞.

Table 2-13  Gaps Between Representable Single-Format Floating-Point Numbers

x nextafter(x, +•) Gap 0.0 1.4012985e–45 1.4012985e–45 1.1754944e–38 1.1754945e–38 1.4012985e–45 1.0 1.0000001 1.1920929e–07 2.0 2.0000002 2.3841858e–07 16.000000 16.000002 1.9073486e–06 128.00000 128.00002 1.5258789e–05 1.0000000e+20 1.0000001e+20 8.7960930e+12 9.9999997e+37 1.0000001e+38 1.0141205e+31

Any conventional set of representable floating-point numbers has the property that the worst effect of one inexact result is to introduce an error no worse than the distance to one of the representable neighbors of the computed result. When subnormal numbers are added to the representable set and gradual underflow is implemented, the worst effect of one inexact or underflowed result is to introduce an error no greater than the distance to one of the representable neighbors of the computed result.

In particular, in the region between zero and the smallest normal number, the distance between any two neighboring numbers equals the distance between zero and the smallest subnormal number. The presence of subnormal numbers eliminates the possibility of introducing a round-off error that is greater than the distance to the nearest representable number.

Because no calculation incurs round-off error greater than the distance to any of the representable neighbors of the computed result, many important properties of a robust arithmetic environment hold, including these three:

• x ≠ y if and only if x – y ≠ 0

• (x – y) + y ≈ x, to within a rounding error in the larger of x and y

• 1/(1/x) ≈ x, when x is a normalized number, implying 1/x ≠ 0 even for the largest normalized x

An alternative underflow scheme is abrupt underflow, which flushes underflow results to zero. Abrupt underflow violates the first and second properties whenever x – y underflows. Also, abrupt underflow violates the third property whenever 1/x underflows.

Let λ represent the smallest positive normalized number, which is also known as the underflow threshold. Then the error properties of gradual underflow and abrupt underflow can be compared in terms of λ.

gradual underflow: |error| < ½ulp in λ

abrupt underflow: |error| ≈ λ

There is a significant difference between half a unit in the last place of λ, and λ itself.