Il bootstrap è una semplice tecnica che consente di stimare l'affidabilità o la precisione delle statistiche di previsione o di altri dati campione. I metodi tradizionali si basano su formule matematiche per descrivere la precisione delle statistiche campione. Quando la distribuzione di campionamento di una statistica non è distribuita normalmente o non è facilmente individuabile, questi metodi classici sono difficili da utilizzare o non sono validi.
Lo strumento Bootstrap analizza le statistiche campione campionando ripetutamente i dati e creando distribuzioni delle diverse statistiche di ogni campionamento. Il metodo bootstrap utilizza la distribuzione delle statistiche per analizzare la precisione delle statistiche stesse.
Con questo strumento sono disponibili due metodi bootstrap:
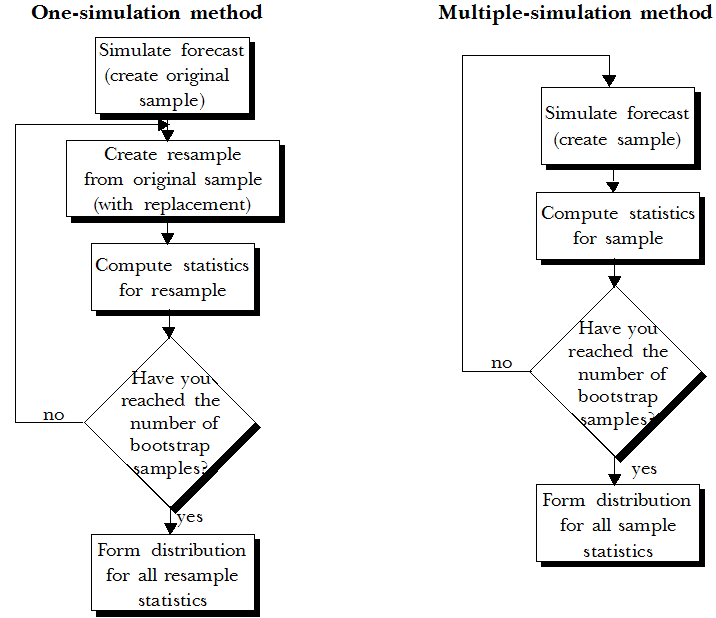
Metodo basato su simulazione unica: esegue la simulazione dei dati del modello una sola volta (creando il campione originale) e quindi ripete continuamente il campionamento di tali prove di simulazione (i valori campione originali). Il ricampionamento crea un nuovo campione dal campione originale sostituendo i valori. In altre parole, restituisce il valore selezionato al campione prima di selezionare un altro valore, lasciando al selettore la possibilità di riselezionare lo stesso valore. Crea quindi una distribuzione delle statistiche calcolate da ogni nuova campionatura. Questo metodo presuppone solo che i dati della simulazione originale descrivano accuratamente la vera distribuzione di previsione, cosa probabile se il campione è sufficientemente grande. Questo metodo non garantisce la stessa precisione del metodo basato su più simulazioni, ma ha un tempo di esecuzione decisamente inferiore.
Metodo basato su più simulazioni: ripete continuamente la simulazione del modello, quindi crea una distribuzione delle statistiche di ogni simulazione. Questo metodo garantisce una maggiore precisione rispetto al metodo basato su simulazione unica, ma il tempo di esecuzione può essere proibitivo.
Quando si utilizza il metodo basato su più simulazioni, lo strumento disattiva temporaneamente l'opzione Usa stessa sequenza di numeri casuali. Nella documentazione relativa alle statistiche il metodo basato su simulazione singola è denominato anche bootstrap non parametrico, mentre il metodo basato su più simulazioni è denominato anche bootstrap parametrico. |
Poiché la tecnica bootstrap non presuppone che il campionamento sia distribuito normalmente, è possibile utilizzarla per stimare la distribuzione di campionamento di qualsiasi statistica, persino una non convenzionale come il valore minimo o massimo di una previsione. È inoltre possibile stimare facilmente statistiche complesse, come il coefficiente di correlazione di due set di dati, o combinazioni di statistiche, come il rapporto di una media rispetto a una varianza.
Per stimare la precisione di statistiche Ipercubo latino, è necessario utilizzare il metodo basato su più simulazioni.