ブートストラップは、予測統計量または他のサンプル・データの信頼性または精度を推定する単純な手法です。従来の手法は、サンプル統計量の精度を表すために数学的な式に頼っています。統計量のサンプリング分布が正規分布でない場合や簡単に特定できない場合、このような従来の手法は使用が困難になるか、無効になります。
ブートストラップの場合、データを繰り返しサンプリングし、各サンプリングから異なる統計量の分布を作成することにより、サンプル統計量を分析します。この手法は、統計量自体の分布を使用して統計量の精度を分析するため、「自分でブーツのつまみ革を引っ張り上げる」という意味を持つ「ブートストラップ」という名前が付けられました。
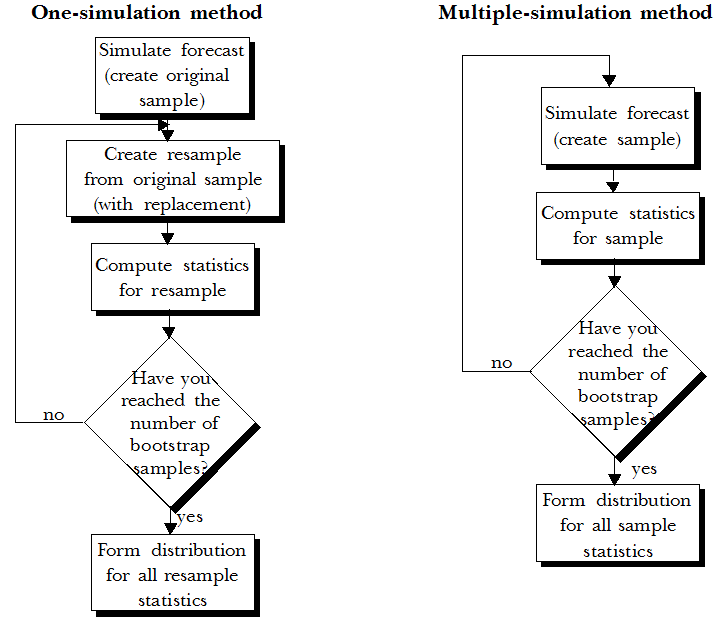
単一シミュレーション手法 - モデル・データを1回シミュレート(元のサンプルを作成)した後、これらのシミュレーション試行(元のサンプル値)を繰り返し再サンプリングします。再サンプリングでは、置換を行いながら元のサンプルから新規サンプルを作成します。つまり、別の値を選択する前に選択した値をサンプルに返すことにより、セレクタが同じ値を再選択できるようにします。これにより、各再サンプルから計算された統計量の分布が作成されます。この手法では、元のシミュレーション・データが正確な予測分布を表すことのみを前提としていますが、サンプルが十分大きければこのようになる可能性は高くなります。この手法は複数シミュレーション手法ほど正確ではありませんが、処理時間は大幅に短縮されます。
複数シミュレーション手法 - モデルを繰り返しシミュレートした後、各シミュレーションから統計量の分布を作成します。この手法の方が単一シミュレーション手法より正確ですが、処理時間が非常に長くなる可能性があります。
複数シミュレーション手法を使用する場合、「同じ乱数シーケンスを使用」オプションが一時的にオフになります。統計用語では、単一シミュレーション手法は非パラメトリック・ブートストラップとも呼ばれ、複数シミュレーション手法はパラメトリック・ブートストラップとも呼ばれます。 |
ブートストラップ手法ではサンプリング分布が正規分布であることを前提としていませんが、この手法を使用して、任意の統計量のサンプリング分布を推定することができます。これは、予測の最小値または最大値などの従来とは異なる統計量の場合でも可能です。また、2つのデータ・セットの相関係数などの複雑な統計量や、平均値と分散の比率などの統計量の組合せも簡単に推定することができます。