2Dシミュレーション分析の例では、Crystal Ballモデルの例、Toxic Waste Site.xlsxを使用します(図9.15「毒性廃棄物処理場のスプレッドシート・モデル」)。このモデルでは、毒性廃棄物処理場による住民への癌のリスクを予測します。このスプレッドシートには、2つの可変性仮定と2つの不確実性仮定があります。
結果を生成するために、同じ乱数シーケンスおよびシード値999を使用して最初にCrystal Ballの実行プリファレンスをモンテ・カルロ・シミュレーションに設定します。次に、リスク評価を対象予測として2次元シミュレーション・ツールを実行します。この際、「仮定タイプ」パネルの可変性リストに体重および1日当たりの水量を含め、次のオプション設定を使用します:
2次元シミュレーション・ツールを実行すると、最初に1試行ずつ単一ステップで実行され、不確実性仮定の値セットが生成されます。次に、これらの仮定が固定され、内部ループで可変性仮定のシミュレーションが実行されます。
内部ループの実行ごとにCrystal Ballの予測情報が取得されます。次に、シミュレーションがリセットされ、外部ループが指定されたシミュレーション回数実行されるまでプロセスが繰り返されます。
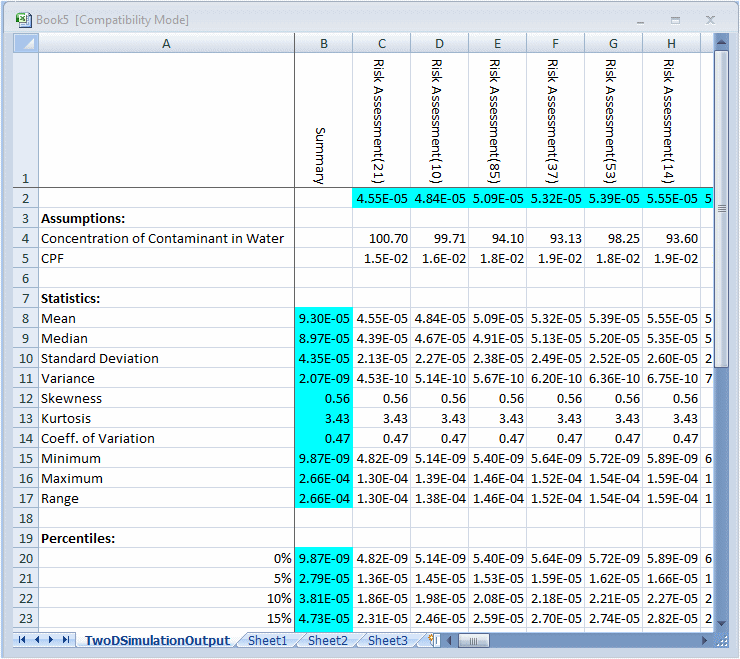
シミュレーションの結果は、各シミュレーションの予測分布の予測平均値、不確実性仮定値および統計量(パーセンタイルを含む)が含まれる表に表示されます(図9.18「2次元シミュレーションの結果表」)。
また、2次元シミュレーションの結果は重ねグラフおよび傾向グラフにもグラフ化されます。
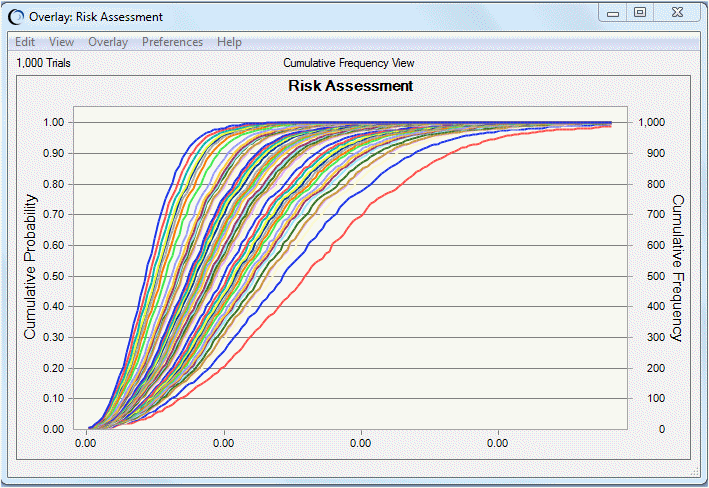
重ねグラフのプリファレンスでは、不確実性仮定値の別セットのシミュレーションのリスク曲線を表示するよう設定できます。これを行うには、各系列の「グラフ・タイプ」を「折れ線」に設定し、「累積度数」ビューを選択します。グラフのホットキー(グラフ・タイプには[Ctrl]キーを押しながら[T]キーを押し、ビューには[Ctrl]キーを押しながら[D]キーを押す)使用すると便利です。オプションで、[Ctrl]キーを押しながら[N]キーを押して凡例を移動または除去したり、[Ctrl]キーを押しながら[M]キーを押して中央の傾向補助線を切り替えます。
この例の図9.19「リスク曲線の重ねグラフ」では、ほとんどのリスク曲線が中央に密集しているものの、いくつかの外れ曲線は「累積度数」軸の方に分散しており、リスクがより高くなる確率がわずかにあることを示しています。
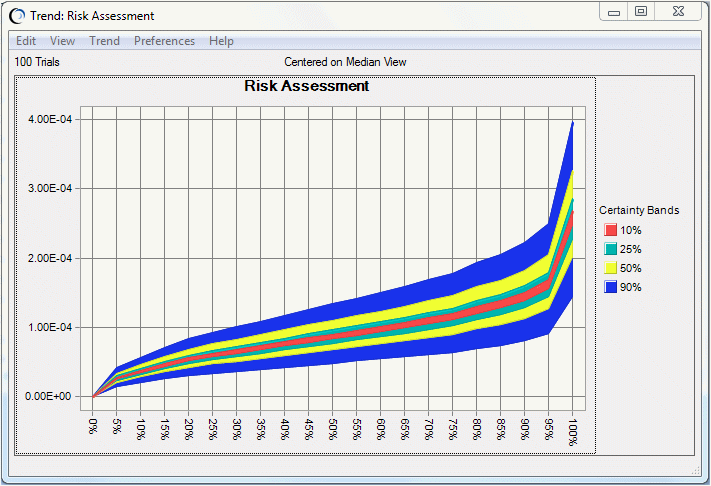
傾向グラフ(図9.20「傾向グラフの信頼度の帯」)は、リスク曲線のパーセンタイルの信頼度の帯を示しています。帯の幅は、すべての分布における各パーセンタイル・レベルの不確実性の量を表します。
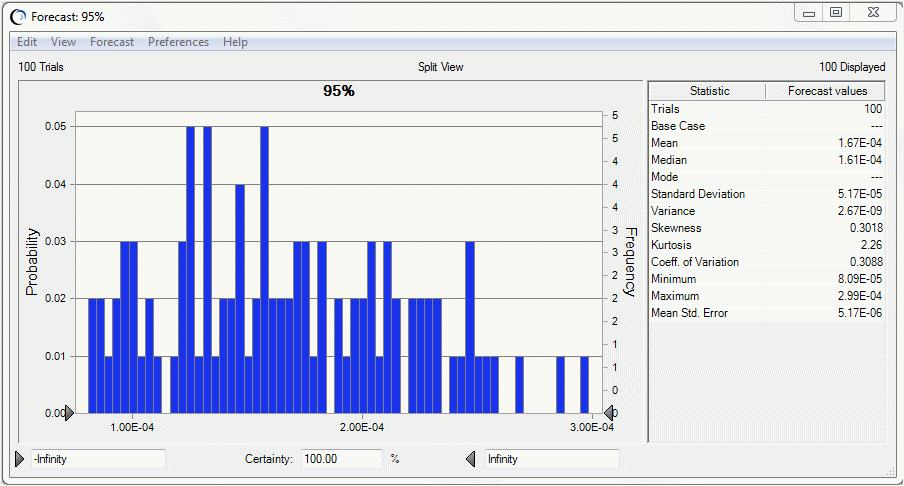
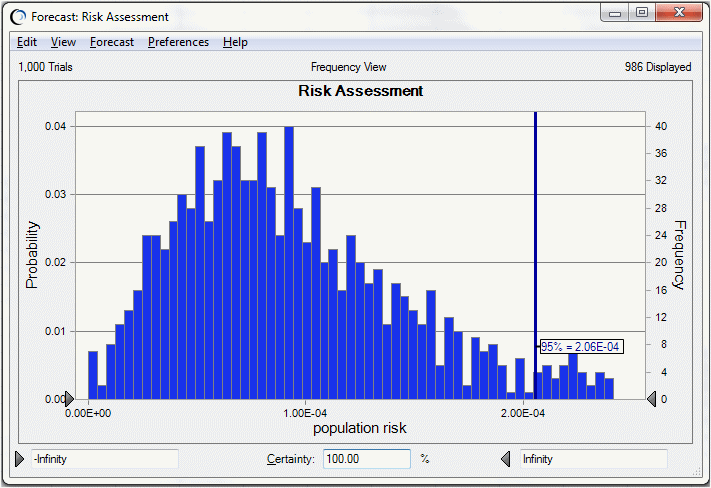
95番目のパーセンタイルなどの特定のパーセンタイル・レベルにフォーカスを置くには、図9.21「95番目のパーセンタイル予測の統計量」に示すように、95番目のパーセンタイル予測の統計量を表示します。たとえば、この図は、100回の試行、予測内の95番目のパーセンタイルの数値を示しています。
図9.22「1次元シミュレーションの予測グラフ」に示す、同じリスク・モデルの1次元シミュレーション(不確実性と可変性の両方が混在しています)と、2次元シミュレーションの結果を比較してください。
図9.21「95番目のパーセンタイル予測の統計量」の95番目のパーセンタイル1.45E-4は、図9.22「1次元シミュレーションの予測グラフ」に示される1次元シミュレーションの95番目のパーセンタイル・リスク2.06E-4より低くなっています。これは、1次元シミュレーションの傾向の結果として住民のリスクが(特に大きく歪んだ分布の場合)過大評価されることを示します。
多くの場合、仮定のパラメータは相関します。たとえば、高い平均値を高い標準偏差と相関させたり、低い平均値を低い標準偏差と相関させます。パラメータ分布間で相関係数を定義することにより、2次元シミュレーションの精度を向上させることができます。住民の体重サンプルの場合のようにデータが使用可能な場合、ブートストラップ・ツールを使用して、パラメータのサンプリング分布およびこれらの相関を推定することができます。 |
2次仮定
一部の仮定には、不確実性と可変性の両方の要素が含まれます。たとえば、仮定によって住民の体重の分布を表すことができますが、分布パラメータは不明である場合があります。このようなタイプの仮定は2次仮定(または2次ランダム変数; 参照: BurmasterおよびWilson、1996年、参考文献一覧内)と呼ばれます。このようなタイプの仮定をCrystal Ballでモデリングするには、分布の不確実性パラメータを別のセルに配置し、これらのセルを仮定として定義します。次に、セル参照を使用して可変性仮定のパラメータを不確実性仮定にリンクします。
 これをToxic Waste Site.xlsxスプレッドシートについて図で示す手順:
これをToxic Waste Site.xlsxスプレッドシートについて図で示す手順:
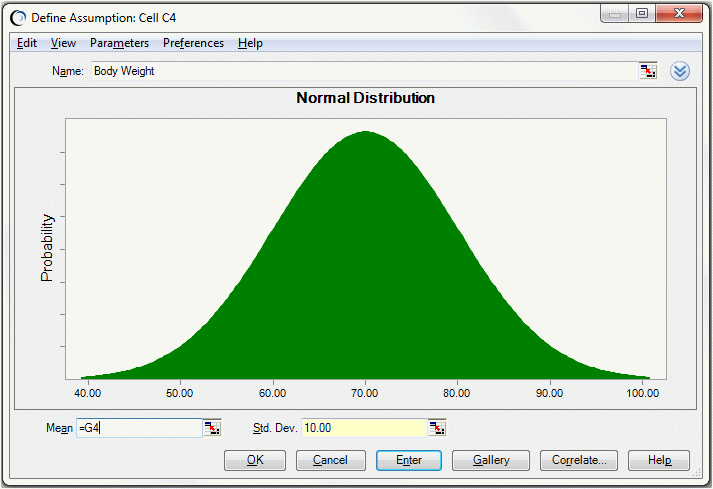
セルG4およびH4に値
70および10をそれぞれ入力します。平均値70および標準偏差2の正規分布を使用してセルG4に仮定を定義します。
平均値10および標準偏差1の正規分布を使用してセルH4に仮定を定義します。
体重仮定でこれらのセルに対する参照を入力します(図9.23「平均値および標準偏差に対するセル参照を使用した仮定」)。
2次仮定に対してツールを実行すると、仮定のパラメータの不確実性が外部シミュレーションでモデリングされ、仮定自体の分布が(異なるパラメータ・セットで)内部シミュレーションでモデリングされます。