データの探索

機械翻訳について

データの探索

データを探索すると、変数を個別に理解し、それらがどのように相互作用するかを理解するのに役立ちます。

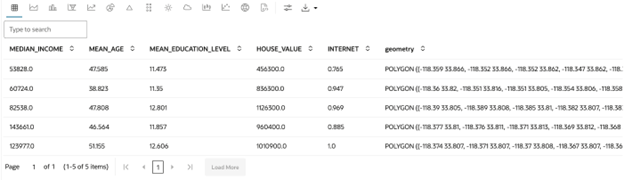
データを探索するには、次のステップを実行します:

headメソッドを使用して、トレーニング・セットの最初の5つの観測を視覚化してデータを理解します。
```
from oraclesai import enable_geodataframes
enable_geodataframes(z)

z.show(X_train.head())
```
出力は次のようになります:

図regression_explore_data_head_method.pngの説明
空間ウェイトを定義して、隣接するロケーションにおける各変数の影響を把握します(隣接するロケーション間の関係を確立します)。
K-Nearest Neighborアプローチを使用します。これは、各観察について、最も近いK観測が隣接とみなされることを示します。
```
from oraclesai.weights import KNNWeightsDefinition

weights_definition = KNNWeightsDefinition(k=10)
```
空間ラグを計算して、隣接するロケーションとの相互作用を調べます。
観察の空間ラグは、隣接する特定の特徴の平均値を表します。たとえば、近隣地域全体の平均住宅価値です。

次のコードでは、ジオメトリを除く、トレーニング・セット内のすべての変数の空間ラグを計算します。
```
from oraclesai.preprocessing import SpatialLagTransformer 

X_spatial_lag = SpatialLagTransformer(weights_definition).fit_transform(X_train)
```
トブラーの最初の地理法則によると、「すべては他のものと関係があるが、近いものは遠いものと関係がある」。特定のロケーションのフィーチャ間の関係を理解するには、フィーチャと空間ラグの相関関係を使用します。たとえば、中央所得と近隣地域からの平均所得との強い正の相関関係は、近隣地域からの中央所得に影響を及ぼす可能性があります。

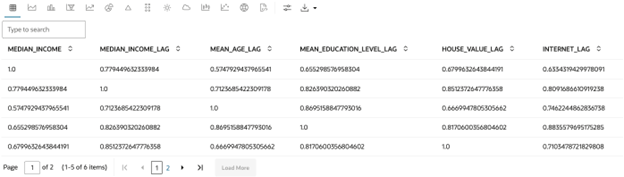
次のコードは、空間ラグ変数とターゲット変数の相関マトリックスを表示します。このとき、空間ラグ変数にはサフィクス_LAGが付きます。
```
import numpy as np
import pandas as pd 

# Append the target variable to the spatial lag variables 
X_target_spatial_lag = np.append(X_train["MEDIAN_INCOME"].get_values(), X_spatial_lag, 1) 

# Create a Pandas' DataFrame
columns = ["MEDIAN_INCOME", "MEDIAN_INCOME_LAG", "MEAN_AGE_LAG", "MEAN_EDUCATION_LEVEL_LAG", "HOUSE_VALUE_LAG", "INTERNET_LAG"] 
X_target_spatial_lag_df = pd.DataFrame(data=X_target_spatial_lag, columns=columns)

z.show(X_target_spatial_lag_df.corr())
```
出力は次のようになります:

図correlation_matrix.pngの説明
隣人の影響を測る。
ターゲット変数( MEDIAN_INCOME)とその空間ラグ( MEDIAN_INCOME_LAG)の間には強い正の相関関係があります。これは、同じような収入のあるロケーションが一緒になる傾向があることを示しており、これは空間依存のインジケータです。
空間依存性の存在を確認するために、空間自己相関を測定するMoranのI統計を計算します。
- 正の値と有意の値は、空間クラスタリングが存在することを示します。この場合、類似した値(高または低)のリージョンが一緒になり、空間依存性の影響が反映されます。
- 負および有意な値は、空間分散またはチェッカ・ボード・パターンの存在を示し、空間異質性の影響を反映します。
```
from oraclesai.analysis import MoranITest 
from oraclesai.weights import SpatialWeights 
# Create spatial weights from definition 
spatial_weights = SpatialWeights.create(X_train["geometry"].values, weights_definition) 

# Run the Moran's I test 
moran_test = MoranITest.create(X_train, spatial_weights, column_name="MEDIAN_INCOME") 

# Print the Moran's I and the p-value 
print("Moran's I = ", moran_test.i) 
print("p_value = ", moran_test.p_value)
```
MoranのI統計は肯定的で重要であり、ターゲット変数に空間依存が存在することを確認します。
```
Moran's I =  0.5744827266749303
p_value =  0.001
```
空間統計を取得します。
空間診断を使用してOLSモデルを実行すると、一部の空間統計が使用可能になります。空間診断を取得するには、OLSRegressorのインスタンスを作成するときに空間重みを定義する必要があります。
```
from oraclesai.regression import OLSRegressor

ols_model = OLSRegressor(weights_definition).fit(X_train, "MEDIAN_INCOME")
```
oraclesai.metricsのmoran_res metricを使用して、モデルの残余からMoranのI統計を取得します。
```
from oraclesai.metrics import moran_res 

morans_i, _, p_value = moran_res(ols_model) 

print(f"Moran's I = {morans_i}") 
print(f"p_value = {p_value}")
```
Moranの残余のI統計の肯定的かつ有意な値は、残余に空間依存が存在することを示しており、これは、観察の予測誤差がその隣人の予測誤差に似ていることを意味します。
```
Moran's I = 0.2594180201084295
p_value = 9.432690077796932e-203
```
2つの回帰モデル「空間ラグ・モデル」および「空間エラー・モデル」には、回帰方程式における空間依存性の影響が含まれます。

トレーニングを受けたOLSモデルの空間診断からLagrange Multipliersテストを使用して、データに最適なモデルを選択します。 Spatial LagおよびSpatial ErrorのLagrange Multiplierテストは、oraclesai.metricsの一部です。
```
from oraclesai.metrics import lm_lag, lm_error, rlm_lag, rlm_error
 
print(f"Lagrange Multiplier (lag): {lm_lag(ols_model)}")
print(f"Robust LM (lag): {rlm_lag(ols_model)}")
print(f"Lagrange Multiplier (error): {lm_error(ols_model)}")
print(f"Robust LM (error): {rlm_error(ols_model)}")
```
Lagrange MultiplierテストがSpatial LagおよびSpatial Errorにとって重要な場合は、堅牢なテストを使用します。どちらの堅牢なテストも重要ですが、空間エラーの統計の値ははるかに大きく、空間エラー・モデルがデータに適していることを示しています。
```
Lagrange Multiplier (lag): (357.8764476978743, 8.165543828650201e-80)
Robust LM (lag): (10.656323334376838, 0.001096952308135397)
Lagrange Multiplier (error): (904.2345462924114, 1.178375337257614e-198)
Robust LM (error): (557.0144219289139, 3.750470342578867e-123)
```