Tipi di visualizzazioni generati dagli approfondimenti automatici
Gli approfondimenti automatici generano vari tipi di visualizzazioni che forniscono approfondimenti specifici sui dati. Ciascuna di queste visualizzazioni utilizza colonne diverse dei dati e viene classificata in base al valore dell'approfondimento nel contesto dei dati.
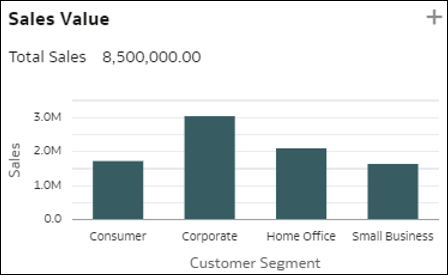
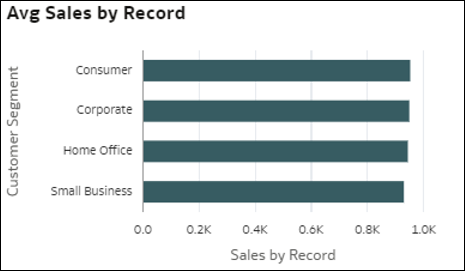
- Dettagli dimensione: queste visualizzazioni aggregano il valore di una misura per i diversi membri di una dimensione nei dati. Questa visualizzazione fornisce una rapida panoramica della distribuzione della metrica selezionata rispetto a una determinata dimensione. La misura può essere costituita da una metrica del data set, un conteggio di record o un valore medio della metrica per record.
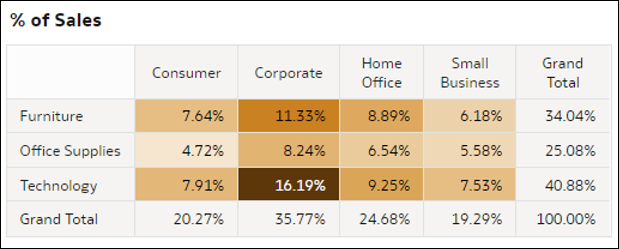
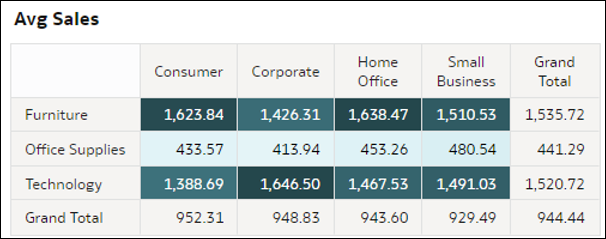
- Tabelle pivot con mappa cromatica: queste visualizzazioni aggregano il valore di una misura per le intersezioni di due dimensioni nei dati. Ogni cella nella tabella pivot rappresenta un'intersezione dei membri di due dimensioni D2 selezionate. Queste visualizzazioni consentono di capire rapidamente dove si trovano i valori più alti della misura osservando le celle più scure delle tabelle. Le misure in questa visualizzazione possono essere costituite da una metrica del data set, un conteggio di record, un valore medio della metrica per record o una percentuale che rappresenta una qualsiasi di queste opzioni (con il totale in alto a destra uguale al 100%).
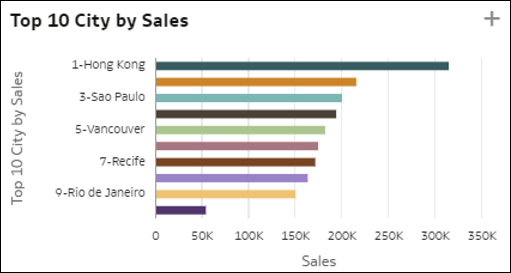
- Primi 10 membri: questa visualizzazione mostra in ordine decrescente i valori dei primi membri di una dimensione per una misura nel data set. L'ultima barra nel grafico mostra il valore medio della misura per tutti i membri non classificati tra i primi nove. In altre parole, il valore medio di M1 per tutti i membri che non sono classificati tra i primi. Queste informazioni indicano la distanza dei primi membri rispetto alla media del resto della popolazione.
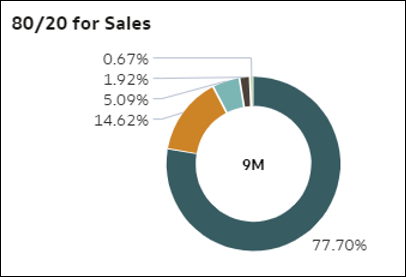
- 80/20: questa visualizzazione mostra, per una determinata misura, la valutazione dell'importanza dei record nel primo 20% dei dati rispetto al data set totale. Il primo 20% viene calcolato in base alle righe dettagliate nel data set. Il grafico ad anelli mostra l'importanza dei primi membri nei dati per tale misura. Gli archi nel grafico ad anelli rappresentano i quintili dei record, ovvero le porzioni consecutive che costituiscono ciascuna il 20% dei record per numero decrescente di righe (i membri del primo 20% seguiti da quelli del successivo 20% e così via). La dimensione degli archi rappresenta il valore aggregato totale della misura per ciascun quartile.
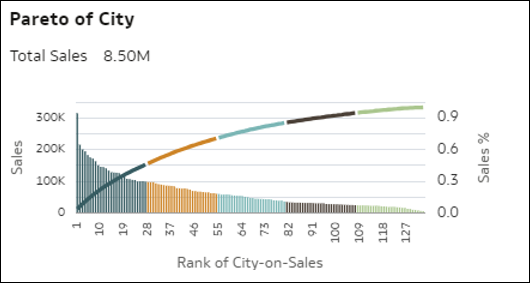
- Pareto: questa visualizzazione del grafico Pareto mostra tutti i membri di una dimensione (cardinalità media) disposti in ordine decrescente in base al valore di una misura. Ogni barra rappresenta questa misura per un membro e la linea rappresenta la percentuale cumulativa del valore della misura (somma dei valori fino a 1.0 = 100%) poiché ogni membro della dimensione viene aggiunto in modo cumulativo. Un grafico Pareto consente di concentrare l'attenzione sulle area con la frequenza o il valore relativo più elevato.
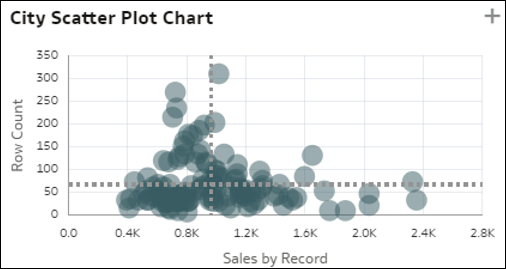
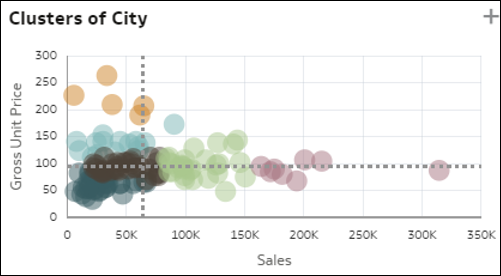
- Grafici a dispersione e cluster: la visualizzazione grafico a dispersione mostra tutti i membri di una dimensione (cardinalità media) su un griglia con due misure distinte dei dati per gli assi. Ogni misura è suddivisa in base al valore unitario medio. La distribuzione tra tutti questi record e i potenziali valori anomali rappresentano approfondimenti interessanti sui membri della dimensione. Questo grafico offre una rapida panoramica della correlazione tra le due metriche per i membri B1 e consente di comprendere facilmente in quale quadrante rientrano i singoli membri. Una variante del grafico a dispersione mostra un raggruppamento automatico dei record in sei gruppi coerenti.
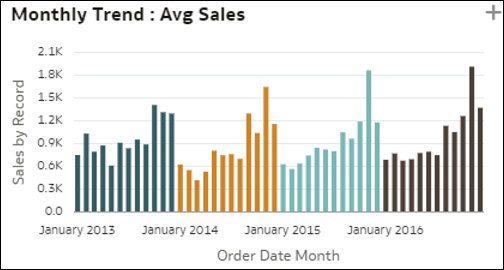
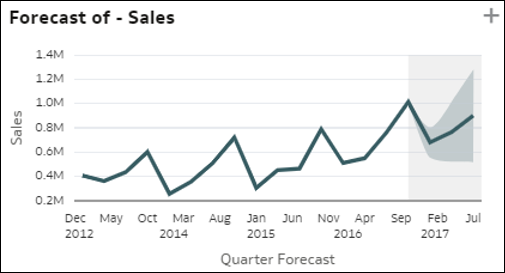
- Grafici a barre delle tendenze semplici: questa visualizzazione rappresenta l'evoluzione delle tendenze di una misura in una colonna temporale del data set. Può mostrare pattern di tendenza interessanti, ad esempio una crescita o una diminuzione. La misura può essere costituita da una metrica del data set, un conteggio di record o un valore medio di una metrica per record. Lo stesso approfondimento può essere visualizzato anche utilizzando una linea di previsione aggiuntiva sul lato destro del grafico.
- Tendenze comparative per dimensione: questa visualizzazione confronta le tendenze del valore di una misura nel tempo per ogni membro di una dimensione nei dati. Ogni linea in questo grafico mostra l'evoluzione di una misura per un determinato membro della dimensione. La crescita o la diminuzione del valore della misura potrebbe non essere coerente per tutti i membri della dimensione. Pertanto, potrebbe risultare interessante sviluppare l'approfondimento su quale membro mostra tendenze diverse rispetto agli altri.
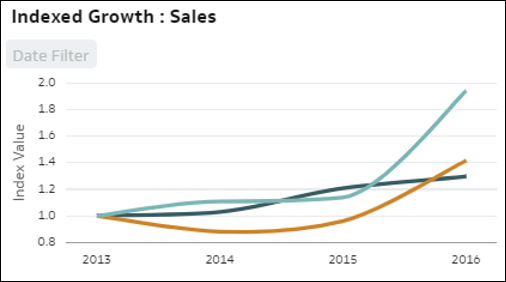
- Tendenze indicizzate comparative: questa visualizzazione confronta la crescita relativa di una misura nel tempo per ogni membro di una colonna dimensione nei dati. Ogni linea rappresenta un membro della dimensione, con un valore di indice di base di 1.00 impostato in un periodo di tempo iniziale. L'evoluzione nel tempo mostra il valore relativo nei periodi successivi rispetto al valore di indice 1.00 nel periodo iniziale. L'uso dell'indicizzazione anziché dei valori assoluti consente di effettuare un confronto equo delle varie tendenze poiché le linee mostrano l'evoluzione relativa effettiva, confrontando correttamente la crescita di ciascun membro. Quando si analizzano i valori assoluti delle metriche anziché i valori indicizzati, le discrepanze nei valori spesso rende impossibile confrontare correttamente la crescita o la diminuzione dei valori. L'utilizzo degli indici consente di comprendere il comportamento relativo effettivo.
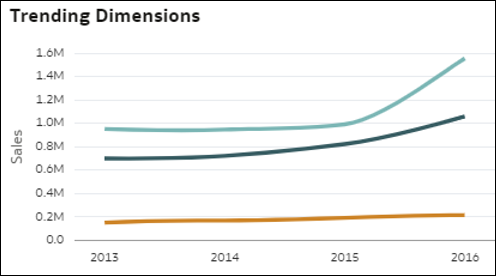
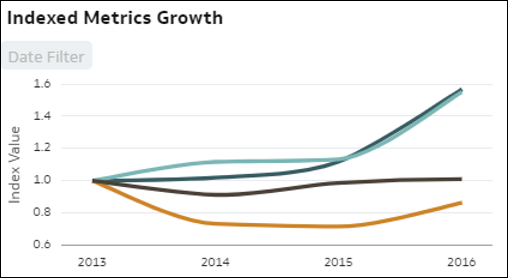
- Tendenze indicizzate in base alle misure: questa visualizzazione confronta l'evoluzione relativa di alcune misure del data set nel tempo. Il grafico a linee visualizza il valore indicizzato di varie metriche del data set nel tempo. Ciascuna linea rappresenta una misura. L'uso dell'indicizzazione anziché dei valori assoluti consente di effettuare un confronto equo delle varie tendenze poiché l'osservazione diretta dei valori assoluti delle metriche spesso rende impossibile confrontare correttamente la crescita o la diminuzione dei valori. Il valore di indice iniziale (1.00) è impostato per tutte le metriche su un periodo di tempo iniziale. La linea mostra l'evoluzione relativa di ogni metrica rispetto al relativo punto iniziale nel grafico (indice).
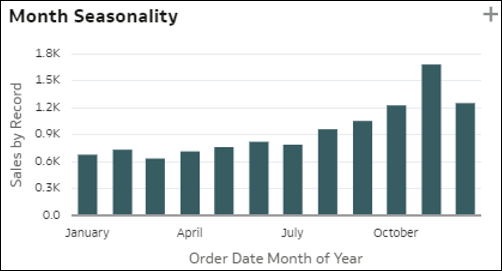
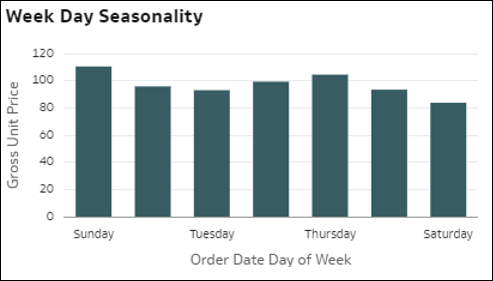
- Stagionalità: le barre in questa visualizzazione rappresentano la distribuzione di una misura in base al mese dell'anno, al giorno del mese o al giorno della settimana di un oggetto temporale nel data set. Questa visualizzazione offre un'indicazione della possibile stagionalità del valore percentuale nei mesi. I grafici della stagionalità sono utili per identificare i pattern ricorrenti nei dati in periodi specifici. Questa visualizzazione può essere importante per comprendere le fluttuazioni stagionali dei valori delle misure.
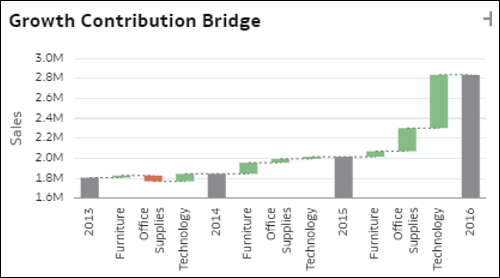
- Grafico a cascata del contributo dei membri: questo grafico mostra il contributo di ciascun membro di una dimensione nel data set alla variazione del valore di una misura nel tempo. È utile per comprendere quali membri hanno contribuito maggiormente a una variazione (aumento o diminuzione) in un periodo di tempo. Ciascun barra grigia nel grafico rappresenta il valore totale di una misura per un periodo di T1. Le barre verdi o rosse tra due periodi indicano quali membri hanno determinato un aumento o una diminuzione e, pertanto, in che modo hanno contribuito alla variazione complessiva.
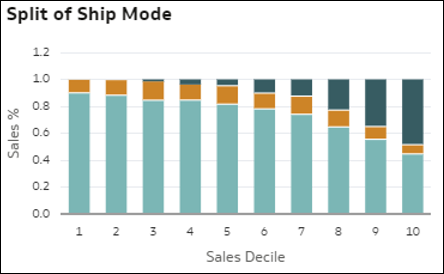
- Suddivisione (combinazione) dei membri della dimensione rispetto al valore della misura: questa visualizzazione consente di comprendere la combinazione (suddivisione) di tutti i membri di una dimensione nei dati quando il valore di una misura cresce. Le barre rappresentano i valori relativi di una misura: Decile 1 = valore basso della misura per record (primo 10% dei record), Decile 2 = secondo 10%, fino al Decile 10 = valore elevato della misura per record. In ciascuna barra i colori mostrano la proporzione (percentuale del totale) di ciascun membro della dimensione rispetto al valore totale della misura per quel determinato decile. Questa visualizzazione aiuta a capire che la struttura della combinazione dei membri varia in funzione della variazione del valore della misura.
- Istogramma di una misura per bin di record: questa visualizzazione mostra la distribuzione di una misura in base ai bin di un'altra misura. Le barre nel grafico mostrano l'aggregazione della misura e ciascuna barra rappresenta un bin per una misura: Bin 1 = valore ridotto della misura per record e Bin 10 = valore elevato della misura per record.
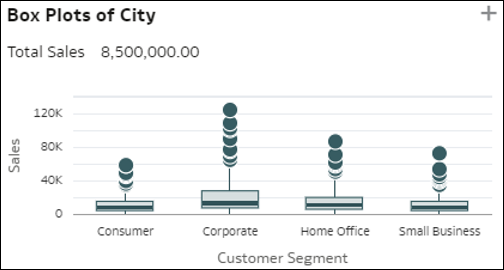
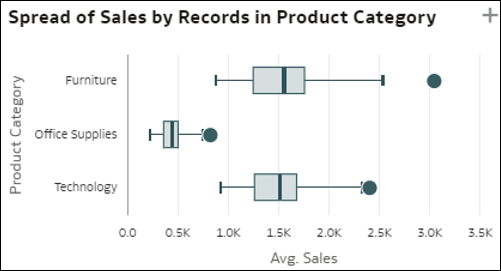
- Box plot dei membri della dimensione: la visualizzazione box plot confronta la distribuzione dei membri in una dimensione D1 (cardinalità media) nei dati (punti) con il valore di una misura nei dati ed è rappresentata da ciascun membro dell'altra dimensione D2 nei dati (barre). Ciascuna barra verticale nel box plot rappresenta un membro di D2 e ciascun punto in una barra è un singolo membro di D1. L'asse Y mostra il valore unitario medio della relativa misura. Ogni barra rappresenta tre valori per questo membro di D2: il valore del primo quartile nella parte inferiore della barra, il valore medio nella parte centrale della barra e il terzo quartile nella parte superiore. Questa visualizzazione è utile per comprendere la distribuzione dei record in una dimensione D1 e confrontare le differenze in tale distribuzione con i membri di una dimensione D2.
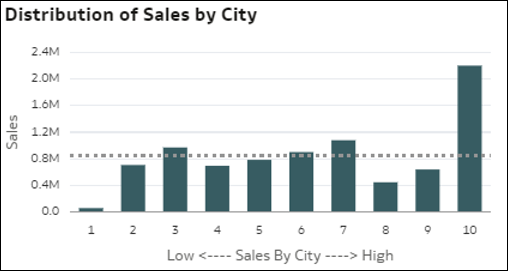
- Distribuzione dei valori dei record in base a una dimensione: questa visualizzazione grafico mostra la dispersione (distribuzione) dei record per il valore di una misura, per ciascun membro di una dimensione (barre). L'asse X mostra il valore medio della misura per record. I puntini in ciascuna barra rappresentano gruppi casuali di record granulari del data set. Questa visualizzazione è utile per comprendere come la distribuzione può variare tra i diversi membri di una dimensione (barre orizzontali differenti nella visualizzazione).
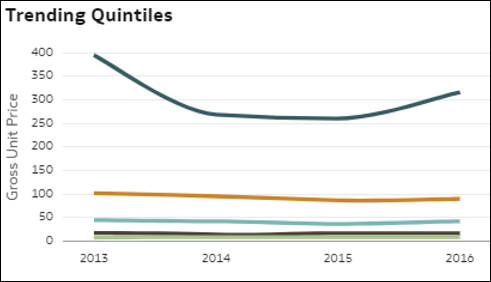
- Confronto delle tendenze di quintili: questa visualizzazione confronta le tendenze nel tempo di ciascun gruppo che costituisce il 20% dei record nei dati (ordinati in base al valore di una misura) dai primi agli ultimi (quintili) per il valore della misura. La crescita o la diminuzione è stata coerente o meno tra i primi e gli ultimi gruppi? Per quale gruppo di popolazione le tendenze della misura sono diverse? Ciascuna linea nel grafico costituisce un quintile che mostra le tendenze nel tempo del valore di M1. I quintili sono gruppi costituiti dal 20% dei record del data set mostrati in ordine decrescente in base al valore della misura: i record con il valore più elevato nel primo 20% sono seguiti da quelli nel successivo 20% e così via.