2 Getting Started with Oracle Text
You can create an Oracle Text developer user account and build simple text query and catalog applications.
This chapter contains the following topics:
2.1 Overview of Getting Started with Oracle Text
This chapter provides basic information about how to configure Oracle Text, how to create an Oracle Text developer user account and how to build simple text query and catalog applications. It also provides information about basic SQL statements for each type of application to load, index, and query tables.
More complete application examples are given in the appendixes.
Note:
The SQL> prompt has been omitted in this chapter, in part to improve readability and in part to make it easier for you to cut and paste text.
See Also:
" Classifying Documents in Oracle Text" to learn more about building document classification applications
2.2 Creating an Oracle Text User
Before you can create Oracle Text indexes and use Oracle Text PL/SQL packages, you need to create a user with the CTXAPP role. This role enables you to do the following:
-
Create and delete Oracle Text indexing preferences
-
Use the Oracle Text PL/SQL packages
To create an Oracle Text application developer user, perform the following steps as the system administrator user:
2.3 Query Application Quick Tour
In a basic text query application, users enter query words or phrases and expect the application to return a list of documents that best match the query. Such an application involves creating a CONTEXT index and querying it with CONTAINS.
Typically, query applications require a user interface. An example of how to build such a query application using the CONTEXT index type is given in CONTEXT Query Application.
The examples in this section provide the basic SQL statements to load the text table, index the documents, and query the index.
2.4 Catalog Application Quick Tour
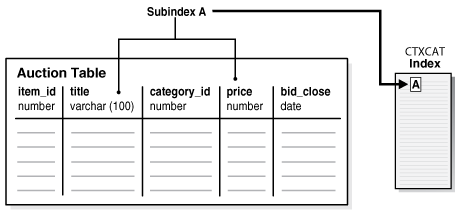
The examples in this section provide the basic SQL statements to create a catalog index for an auction site that sells electronic equipment, such as cameras and CD players. New inventory is added every day, and item descriptions, bid dates, and prices must be stored together.
The application requires good response time for mixed queries. The key is to determine what columns users frequently search to create a suitable CTXCAT index. Queries on this type of index use the CATSEARCH operator.
Note:
Typically, query applications require a user interface. An example of how to build such a query application using the CATSEARCH index type is given in CATSEARCH Query Application .
2.5 Classification Application Quick Tour
The function of a classification application is to perform some action based on document content. These actions can include assigning a category ID to a document or sending the document to a user. The result is classification of a document.
This section contains the following sections:
2.5.1 About Classification of a Document
Documents are classified according to predefined rules. These rules select documents for a category. For instance, a query rule of 'presidential elections' selects documents for a category about politics.
Oracle Text provides several types of classification. One type is simple, or rule-based classification, discussed here, where you create document categories and the rules for categorizing documents. With supervised classification, Oracle Text derives the rules from a set of training documents that you provide. With clustering, Oracle Text does all the work for you, deriving both rules and categories.
To create a simple classification application for document content using Oracle Text, you create rules. Rules are essentially a table of queries that categorize document content. You index these rules in a CTXRULE index. To classify an incoming stream of text, use the MATCHES operator in the WHERE clause of a SELECT statement. See the following image for the general flow of a classification application.
Figure 2-2 Overview of a Document Classification Application

Description of "Figure 2-2 Overview of a Document Classification Application"
See Also: