Define Interest Rate Curve Forecast

2.3.1 Define Interest Rate Curve Forecast

The IRCs for all active currencies (and Reporting Currencies, a subset of the Active Currencies) are listed under Interest Rate Curve Section. The options under Interest Rate Code Forecast Method provide multiple ways to model the effects on Portfolio Cash Flows due to Interest Rate changes.

Figure 2-2 Interest Rate Curve Forecast Rates

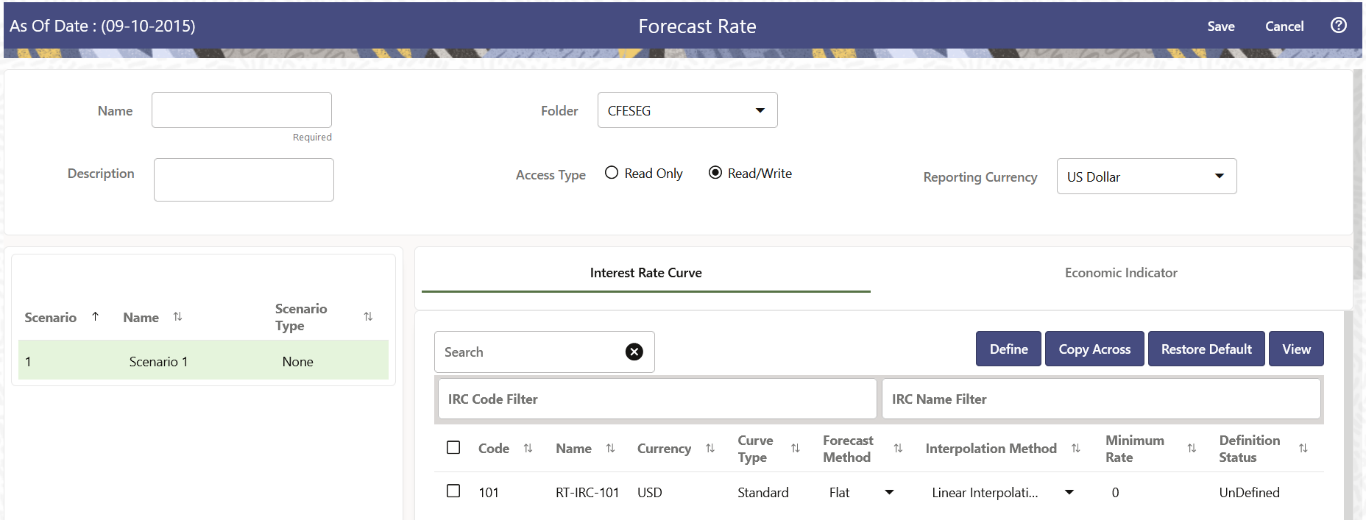
You can define Interest Rate Forecast for the following methods:

Table 2-4 Forecast Rate rule – Methods and Descriptions

Method	Description
Flat	Forecast no change in the Interest Rate for all dates beginning with the As-of Date.
Direct Input	Type Interest Rates directly for any modeling period or Interest Rate term.

The following Interpolation Methods are available.

Table 2-5 Forecast Rate Rule – Interpolation Methods and Descriptions

Method	Description
Linear Interpolation	Linear interpolation uses Linear Yield Curve smoothing. Linear Yield Curves are continuous but not smooth; at each knot point, there is a kink in the yield curve. You may not want to use a Linear Yield Curve with a model that assumes the existence of a continuous Forward Rate Curve, due to the nonlinear and discontinuous knot points of a Linear Yield Curve.
Cubic Spline of Yields	A cubic spline is a series of third-degree polynomials that have the form: y = a + bx + cx2 + dx3 These polynomials are used to connect the dots formed by observable data. The polynomials are constrained so they fit together smoothly at each knot point (the observable data point.) This means that the slope and the rate of change in the slope with respect to time to maturity have to be equal for each polynomial at the knot point where they join. If this is not true, there is a kink in the yield curve and they are continuous but not differentiable. Two more constraints make the Cubic Spline Curve unique. The first restricts the zero-maturity yield to equal the 1-day interest rate. The second restricts the yield curve at the longest maturity to be either straight (y"=0) or flat (y'=0).
Quartic Spline	Quartic interpolation requires a minimum of 4 knot points. The quartic interpolation equation can be represented as: Y = a + bX + cX2 + dX3 + eX4 The end knot points satisfy equations for one curve and all intermediate points satisfy two curves. Therefore, in a scenario with a minimum number of knot points, there are 6 equations. For n number of knot points, the number of equations is 2n-2. If n is the number of points to be interpolated, the order of the matrix to be formed is 5(n-1) x 5(n-1). The matrix is formed according to the following logic: The second derivative at the endpoints and the first derivative of the last point is Zero. At the points other than the endpoints, the value of the first derivatives, second derivatives, and the third derivatives of the function are equal.

Method

Description

Linear Interpolation

Linear interpolation uses Linear Yield Curve smoothing. Linear Yield Curves are continuous but not smooth; at each knot point, there is a kink in the yield curve. You may not want to use a Linear Yield Curve with a model that assumes the existence of a continuous Forward Rate Curve, due to the nonlinear and discontinuous knot points of a Linear Yield Curve.

Cubic Spline of Yields

A cubic spline is a series of third-degree polynomials that have the form:

y = a + bx + cx2 + dx3

These polynomials are used to connect the dots formed by observable data. The polynomials are constrained so they fit together smoothly at each knot point (the observable data point.) This means that the slope and the rate of change in the slope with respect to time to maturity have to be equal for each polynomial at the knot point where they join. If this is not true, there is a kink in the yield curve and they are continuous but not differentiable.

Two more constraints make the Cubic Spline Curve unique. The first restricts the zero-maturity yield to equal the 1-day interest rate. The second restricts the yield curve at the longest maturity to be either straight (y"=0) or flat (y'=0).

Quartic Spline

Quartic interpolation requires a minimum of 4 knot points. The quartic interpolation equation can be represented as:

Y = a + bX + cX2 + dX3 + eX4

The end knot points satisfy equations for one curve and all intermediate points satisfy two curves. Therefore, in a scenario with a minimum number of knot points, there are 6 equations. For n number of knot points, the number of equations is 2n-2. If n is the number of points to be interpolated, the order of the matrix to be formed is 5*(n-1) x 5*(n-1). The matrix is formed according to the following logic:

The second derivative at the endpoints and the first derivative of the last point is Zero. At the points other than the endpoints, the value of the first derivatives, second derivatives, and the third derivatives of the function are equal.

In looking up the Forecast Rates, the Cash Flow Engine (where necessary) performs an interpolation between yield curve term points. For example, in determining a three-month rate from a yield curve that contains only a one-month rate and a six-month rate, the Cash Flow Engine performs an interpolation to determine the implied three-month rate. The Interpolation method used is defined by the selected interpolation method for the Interest Rate Curve.

You can generate the forecast rates for 360 calendar months starting from As-of-Date.

Following options are available for Interest Rate Curve Forecast Rule:

Define

Flat Method
1. Select Interest Rate Code using corresponding checkbox and select Forecast Method as Flat.
2. Select the Interpolation method.
3. Input Minimum Rate, if required.
4. Click Define.
  The status of the Interest Rate Code is changed to Defined.

Direct Input
1. Select Interest Rate Code using corresponding checkbox and select Forecast Method as Direct Input.
2. Select the Interpolation Method.
3. Input Minimum Rate, if required.
4. Click Define.
  The Direct Input window is displayed:
5. Enter data and click Apply.
6. The status of the Interest Rate Code is changed to Defined.

Copy Across

This allows you to copy Forecast Method and related details from one IRC to another.

For example, if you have 10 IRCs enabled in the application and you must input only one set of assumptions, then copy those assumptions across all enabled IRCs, instead of having to input 10 full sets, thereby saving a significant amount of input time.

Flat Method
1. Select Interest Rate Code using corresponding checkbox and select Forecast Method as Flat.
2. Click Copy Across.
3. Click Apply Copy Across.
4. You can click Cancel Copy Across to cancel the Copy Across function.

Note:

You must select a defined IRC. For more information, see the Define section of Interest Rate Curve.

Direct Input
1. Select Interest Rate Code using the corresponding checkbox and select Forecast Method as Direct Input.
  
  Note:
  You must select a defined IRC. For more information, see the Define Section of Interest Rate Curve.
2. Click Copy Across.
3. Click Apply Copy Across.
4. You can click Cancel Copy Across to cancel the Copy Across function.

Restore Default

Use this action to reset previously entered details to Undefined status.

Flat Method
1. Select Interest Rate Code using corresponding checkbox and select Forecast Method as Flat.
2. Click Restore Default.
3. The status of the Interest Rate Code is changed to Undefined.
Direct Input
1. Select Interest Rate Code using corresponding checkbox and select Forecast Method as Direct Input.
2. Click Restore Default.
3. The status of the Interest Rate Code is changed to Undefined.

View

After defining Forecast Method and other parameters for an IRC you can view the forecasted interest rates by clicking this button.

Flat Method
1. Select Interest Rate Code using corresponding checkbox and select Forecast Method as Flat.
2. Click View to see the output table.
Direct Input
1. Select Interest Rate Code using corresponding checkbox and select Forecast Method as Direct Input.
2. Click View to see the Output Table.