2.2.6 Ranges and Precisions in Decimal Representation
This section covers the notions of range and precision for a given storage format. It includes the ranges and precisions corresponding to the IEEE single, double, and quadruple formats and to the implementations of IEEE double-extended format on x86 architectures. For concreteness, in defining the notions of range and precision, refer to the IEEE single format.
The IEEE standard specifies that 32 bits be used to represent a floating-point number in single format. Because there are only finitely many combinations of 32 zeroes and ones, only finitely many numbers can be represented by 32 bits.
It is natural to ask what are the decimal representations of the largest and smallest positive numbers that can be represented in this particular format.
If you introduce the concept of range, you can rephrase the question instead to ask what is the range, in decimal notation, of numbers that can be represented by the IEEE single format?
Taking into account the precise definition of IEEE single format, you can prove that the range of floating-point numbers that can be represented in IEEE single format, if restricted to positive normalized numbers, is as follows:
1.175...× (10-38) to 3.402... ×(10+38)
A second question refers to the precision of the numbers represented in a given format. These notions are explained by looking at some pictures and examples.
The IEEE standard for binary floating-point arithmetic specifies the set of numerical values representable in the single format. Remember that this set of numerical values is described as a set of binary floating-point numbers. The significand of the IEEE single format has 23 bits, which together with the implicit leading bit, yield 24 digits (bits) of (binary) precision.
One obtains a different set of numerical values by marking the numbers (representable by q decimal digits in the significand) on the number line:
x = (x1.x2 x3...xq) × (10n)
The following figure exemplifies this situation:
Figure 2-5 Comparison of a Set of Numbers Defined by Digital and Binary Representation
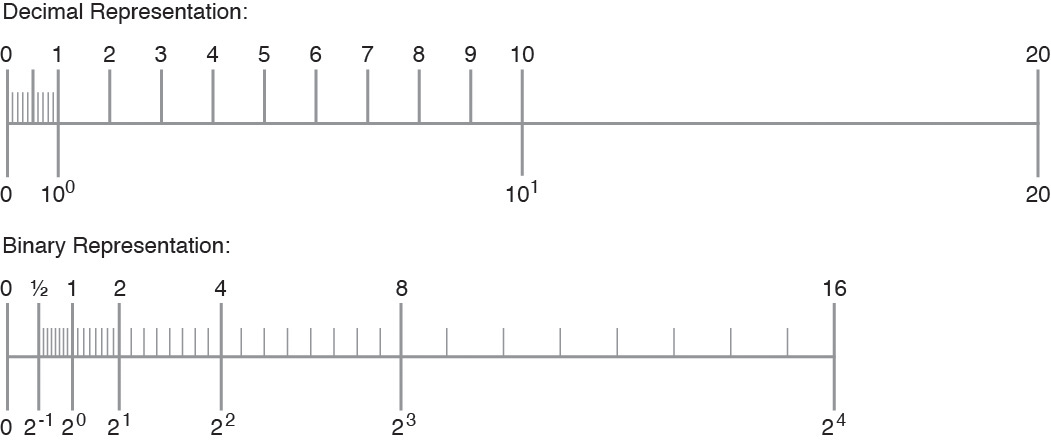
Notice that the two sets are different. Therefore, estimating the number of significant decimal digits corresponding to 24 significant binary digits, requires reformulating the problem.
Reformulate the problem in terms of converting floating-point numbers between binary representations (the internal format used by the computer) and the decimal format (the format users are usually interested in). In fact, you might want to convert from decimal to binary and back to decimal, as well as convert from binary to decimal and back to binary.
It is important to notice that because the sets of numbers are different, conversions are in general inexact. If done correctly, converting a number from one set to a number in the other set results in choosing one of the two neighboring numbers from the second set (which one specifically is a question related to rounding).
Consider some examples. Suppose you are trying to represent a number with the following decimal representation in IEEE single format:
x = x1.x2 x3... × 10n
Because there are only finitely many real numbers that can be represented exactly in IEEE single format, and not all numbers of the above form are among them, in general it will be impossible to represent such numbers exactly. For example, let
y = 838861.2, z = 1.3
and run the following Fortran program:
REAL Y, Z
Y = 838861.2
Z = 1.3
WRITE(*,40) Y
40 FORMAT("y: ",1PE18.11)
WRITE(*,50) Z
50 FORMAT("z: ",1PE18.11)
The output from this program should be similar to the following:
y: 8.38861187500E+05 z: 1.29999995232E+00
The difference between the value 8.388612 × 105 assigned to y and the value printed out is 0.000000125, which is seven decimal orders of magnitude smaller than y. The accuracy of representing y in IEEE single format is about 6 to 7 significant digits, or that y has about six significant digits if it is to be represented in IEEE single format.
Similarly, the difference between the value 1.3 assigned to z and the value printed out is 0.00000004768, which is eight decimal orders of magnitude smaller than z. The accuracy of representing z in IEEE single format is about 7 to 8 significant digits, or that z has about seven significant digits if it is to be represented in IEEE single format.
Assume you convert a decimal floating point number a to its IEEE single format binary representation b, and then translate b back to a decimal number c; how many orders of magnitude are between a and a - c?
Rephrase the question:
What is the number of significant decimal digits of a in the IEEE single format representation, or how many decimal digits are to be trusted as accurate when one represents x in IEEE single format?
The number of significant decimal digits is always between 6 and 9, that is, at least 6 digits, but not more than 9 digits are accurate (with the exception of cases when the conversions are exact, when infinitely many digits could be accurate).
Conversely, if you convert a binary number in IEEE single format to a decimal number, and then convert it back to binary, generally, you need to use at least 9 decimal digits to ensure that after these two conversions you obtain the number you started from.
The complete picture is given in Table 2–10:
|