2.3.5 Two Examples of Gradual Underflow Versus Abrupt Underflow

The following are two well-known mathematical examples. The first example is code that computes an inner product.

sum = 0; 
for (i = 0; i < n; i++) {
 sum = sum + a[i] * y[i]; 
} 
return sum;

With gradual underflow, the result is as accurate as round-off allows. In abrupt underflow, a small but nonzero sum could be delivered that looks plausible but is much worse. However,it must be admitted that to avoid just these sorts of problems, clever programmers scale their calculations if they are able to anticipate where minuteness might degrade accuracy.

The second example, deriving a complex quotient, is not amenable to scaling:

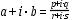assuming |r / s|≤1

.

It can be shown that, despite round-off, the computed complex result differs from the exact result by no more than what would have been the exact result if p + i • q and r + i • s each had been perturbed by no more than a few ulps. This error analysis holds in the face of underflows, except that when both a and b underflow, the error is bounded by a few ulps of |a + i • b| Neither conclusion is true when underflows are flushed to zero.

This algorithm for computing a complex quotient is robust, and amenable to error analysis, in the presence of gradual underflow. A similarly robust, easily analyzed, and efficient algorithm for computing the complex quotient in the face of abrupt underflow does not exist. In abrupt underflow, the burden of worrying about low-level, complicated details shifts from the implementer of the floating-point environment to its users.

The class of problems that succeed in the presence of gradual underflow, but fail with abrupt underflow, is larger than the users of abrupt underflow might realize. Many of the frequently used numerical techniques fall in this class, such as the following:

• Linear equation solving

• Polynomial equation solving

• Numerical integration

• Convergence acceleration

• Complex division