| Skip Navigation Links | |
| Exit Print View | |
|
Oracle Solaris Studio 12.3: C User's Guide Oracle Solaris Studio 12.3 Information Library |
| Skip Navigation Links | |
| Exit Print View | |
|
Oracle Solaris Studio 12.3: C User's Guide Oracle Solaris Studio 12.3 Information Library |
1. Introduction to the C Compiler
2. C-Compiler Implementation-Specific Information
3.1 Overview of Parallelization
3.2.1 Handling OpenMP Runtime Warnings
3.2.3 Using restrict in Parallel Code
3.3 Data Dependence and Interference
3.3.1 Parallel Execution Model
3.5 Load Balance and Loop Scheduling
3.5.1 Static or Chunk Scheduling
3.7 Aliasing and Parallelization
3.7.1 Array and Pointer References
7. Converting Applications for a 64-Bit Environment
8. cscope: Interactively Examining a C Program
A. Compiler Options Grouped by Functionality
B. C Compiler Options Reference
C. Implementation-Defined ISO/IEC C99 Behavior
E. Implementation-Defined ISO/IEC C90 Behavior
H. Oracle Solaris Studio C: Differences Between K&R C and ISO C
The C compiler performs analysis on loops in programs to determine whether executing different iterations of the loops in parallel is safe. The purpose of this analysis is to determine whether any two iterations of the loop could interfere with each other. Typically, this problem occurs if one iteration of a variable could read a variable while another iteration is writing the very same variable. Consider the following program fragment:
Example 3-1 Loop With Dependence
for (i=1; i < 1000; i++) {
sum = sum + a[i]; /* S1 */
}
In this example, any two successive iterations, i and i+1, will write and read the same variable sum. Therefore, in order for these two iterations to execute in parallel some form of locking on the variable would be required. Otherwise, allowing the two iterations to execute in parallel is not safe.
However, the use of locks imposes overhead that might slowdown the program. The C compiler will not ordinarily parallelize the loop in the example above because there is a data dependence between two iterations of the loop. Consider another example:
Example 3-2 Loop Without Dependence
for (i=1; i < 1000; i++) {
a[i] = 2 * a[i]; /* S1 */
}
In this case, each iteration of the loop references a different array element. Therefore different iterations of the loop can be executed in any order. They may be executed in parallel without any locks because no two data elements of different iterations can possibly interfere.
The analysis performed by the compiler to determine whether two different iterations of a loop could reference the same variable is called data dependence analysis. Data dependences prevent loop parallelization if one of the references writes to the variable. The dependence analysis performed by the compiler can have three outcomes:
There is a dependence, in which case, executing the loop in parallel is not safe.
There is no dependence, in which case the loop may safely execute in parallel using an arbitrary number of processors.
The dependence cannot be determined. The compiler assumes, for safety, that a dependence might prevent parallel execution of the loop and will not parallelize the loop.
In the following example, whether two iterations of the loop write to the same element of array a depends on whether array b contains duplicate elements. Unless the compiler can determine this fact, it must assume there might be a dependence and not parallelize the loop.
Example 3-3 Loop That Might Contain Dependencies
for (i=1; i < 1000; i++) {
a[b[i]] = 2 * a[i];
}
The parallel execution of loops is performed by Solaris threads. The thread starting the initial execution of the program is called the master thread. At program start-up the master thread creates multiple slave threads as shown in the following figure. At the end of the program all the slave threads are terminated. Slave thread creation is performed exactly once to minimize the overhead.
Figure 3-1 Master and Slave Threads
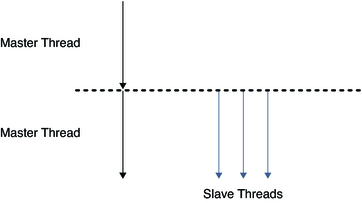
After startup, the master thread starts the execution of the program while slave threads wait idly. When the master thread encounters a parallel loop, different iterations of the loop are distributed among the slave and master threads which start the execution of the loop. After each thread finishes execution of its chunk, it synchronizes with the remaining threads. This synchronization point is called a barrier. The master thread cannot continue executing the remainder of the program until all the threads have finished their work and reached the barrier. The slave threads go into a wait state after the barrier waiting for more parallel work, and the master thread continues to execute the program.
During this process, various overheads can occur:
Synchronization and work distribution
Barrier synchronization
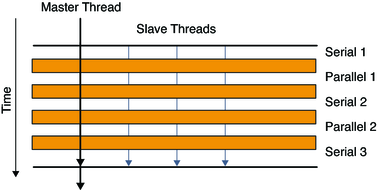
For some parallel loops, the amount of useful work performed is not enough to justify the overhead. For such loops, there may be appreciable slowdown. In the following figure, a loop is parallelized. However the barriers, represented by horizontal bars, introduce significant overhead. The work between the barriers is performed serially or in parallel as indicated. The amount of time required to execute the loop in parallel is considerably less than the amount of time required to synchronize the master and slave threads at the barriers.
Figure 3-2 Parallel Execution of a Loop
For some data dependences, the compiler might still be able to parallelize a loop. Consider the following example.
Example 3-4 Parallelizable Loop With Dependence
for (i=1; i < 1000; i++) {
t = 2 * a[i]; /* S1 */
b[i] = t; /* S2 */
}
In this example, assuming that arrays a and b are non-overlapping arrays, there appears to be a data dependence in any two iterations due to the variable t. The following statements execute during iterations one and two.
Example 3-5 Iterations One and Two
t = 2*a[1]; /* 1 */ b[1] = t; /* 2 */ t = 2*a[2]; /* 3 */ b[2] = t; /* 4 */
Because statements one and three modify the variable t, the compiler cannot execute them in parallel. However, because the value of t is always computed and used in the same iteration, the compiler can use a separate copy of t for each iteration. This method eliminates the interference between different iterations due to such variables. In effect, variable t is used as a private variable for each thread executing that iteration, as shown in the following example.
Example 3-6 Variable t as a Private Variable for Each Thread
for (i=1; i < 1000; i++) {
pt[i] = 2 * a[i]; /* S1 */
b[i] = pt[i]; /* S2 */
}
In this example, each scalar variable reference t is replaced by an array reference pt. Each iteration now uses a different element of pt, eliminating any data dependencies between any two iterations. One problem with this is that it may lead to an extra large array. In practice, the compiler only allocates one copy of the variable for each thread that participates in the execution of the loop. Each such variable is, in effect, private to the thread.
The compiler can also privatize array variables to create opportunities for parallel execution of loops. Consider the following example:
Example 3-7 Parallelizable Loop With an Array Variable
for (i=1; i < 1000; i++) {
for (j=1; j < 1000; j++) {
x[j] = 2 * a[i]; /* S1 */
b[i][j] = x[j]; /* S2 */
}
}
In this example, different iterations of the outer loop modify the same elements of array x, and thus the outer loop cannot be parallelized. However, if each thread executing the outer loop iterations has a private copy of the entire array x, then no interference between any two iterations of the outer loop would occur. The following example illustrates this point.
Example 3-8 Parallelizable Loop Using a Privatized Array
for (i=1; i < 1000; i++) {
for (j=1; j < 1000; j++) {
px[i][j] = 2 * a[i]; /* S1 */
b[i][j] = px[i][j]; /* S2 */
}
}
As in the case of private scalars, you need to expand the array only up to the number of threads executing in the system. This expansion is done automatically by the compiler by allocating one copy of the original array in the private space of each thread.
Privatization of variables can be very useful for improving the parallelism in the program. However, if the private variable is referenced outside the loop then the compiler needs to verify that it has the right value. Consider the following example:
Example 3-9 Parallelized Loop Using Storeback
for (i=1; i < 1000; i++) {
t = 2 * a[i]; /* S1 */
b[i] = t; /* S2 */
}
x = t; /* S3 */
In this example, the value of t referenced in statement S3 is the final value of t computed by the loop. After the variable t has been privatized and the loop has finished executing, the right value of t needs to be stored back into the original variable. This process is called storeback, and is accomplished by copying the value of t on the final iteration back to the original location of variable t. In many cases the compiler can do this automatically, but sometimes the last value cannot be computed easily.
Example 3-10 Loop That Cannot Use Storeback
for (i=1; i < 1000; i++) {
if (c[i] > x[i] ) { /* C1 */
t = 2 * a[i]; /* S1 */
b[i] = t; /* S2 */
}
}
x = t*t; /* S3 */
For correct execution, the value of t in statement S3 is not, usually the value of t on the final iteration of the loop. In fact, it is the last iteration for which the condition C1 is true. Computing the final value of t can be difficult in general. In cases like this example, the compiler will not parallelize the loop.
There are cases when there is a real dependence between iterations of a loop that cannot be removed by simply privatizing the variables causing the dependence. For example, look at the following code where values are being accumulated from one iteration to the next.
Example 3-11 Loop That Might Be Parallelized
for (i=1; i < 1000; i++) {
sum += a[i]*b[i]; /* S1 */
}
In this example,, the loop computes the vector product of two arrays into a common variable called sum. This loop cannot be parallelized in a simple manner. The compiler can take advantage of the associative nature of the computation in statement S1 and allocate a private variable called psum[i] for each thread. Each copy of the variable psum[i] is initialized to 0. Each thread computes its own partial sum in its own copy of the variable psum[i]. Before crossing the barrier, all the partial sums are added onto the original variable sum. In this example, the variable sum is called a reduction variable because it computes a sum-reduction. However, one danger of promoting scalar variables to reduction variables is that the manner in which rounded values are accumulated can change the final value of sum. The compiler performs this transformation only if you specifically give permission for it to do so.