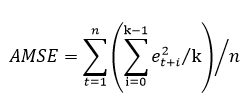13 時系列
Oracle Machine Learning for SQLの回帰機能としての時系列について学習します。
13.1 時系列について
時系列は、既知のターゲット値履歴のみに基づいてターゲット値を予測する機械学習手法です。これは、特殊な形式の回帰であり、文献では自己回帰モデリングと呼ばれています。
時系列分析への入力は、一連のターゲット値です。ケースID列は、順序の並びを指定します。ケースIDは、NUMBER型または日付型(date、datetime、timestamp with timezone、timestamp with local timezone)にできます。ケースIDの型を問わず、ユーザーは予測計算でモデルに傾向または季節的影響、またはその両方を含めるよう要求できます。ケースIDが日付型である場合、ユーザーは、ターゲット値を集計する時間間隔(たとえば、月)と集計手段(たとえば、sum)を指定する必要があります。集計は、モデルを構築する前に、アルゴリズムによって実行されます。
時系列モデルは、ある期間の各ステップのターゲット値の推定値を提供します。期間には、履歴データに加え最大30ステップまで含めることができます。他の回帰モデルと同様に、時系列モデルは、履歴データへの適合度を測定する様々な統計を計算します。
-
革新による成長率や戦略的効果などの投資利益率を予測する
-
コスト、在庫要件、顧客満足度の予測などの戦術的問題に対処する
-
運用目標を設定し、標準への品質と適合性を予測する
関連項目
13.2 時系列モデルの選択
時系列モデルの選択方法について学習します。
時系列データには、予測精度に影響する可能性のあるパターンが含まれていることがあります。たとえば、経済成長期には、売上高が増加傾向にある可能性があります。特定の季節に売上高が増加する可能性があります(夏季の水着など)。このような系列に対応するには、傾向、季節的影響、またはその両方を組み込んだモデルを選択することが有効です。
傾向を単一の定数で表す必要がある場合は、傾向の推定が難しい場合があります。たとえば、成長率が10%である場合、その値は7ステップ後に倍になります。少ない時間ステップに適したローカル成長率は、そのようなレベルに簡単に対処できますが、その後低下してしまします。減衰傾向モデルは、累積する傾向効果を低減することによって、このようなデータをより正確に表すことができます。減衰傾向のモデルは、履歴データに対する傾向効果の変動性をよりよく表すことができます。減衰傾向のモデルは、データに大きな傾向があるが、変動傾向である場合に適しています。
ノート:
乗算誤差は、ゼロまたは負の値を含むデータには適切ではありません。したがって、データにこのような値が含まれている場合は、乗算効果を持つモデルを選択するか、誤差タイプを乗算に設定することをお薦めします。13.3 時系列の統計
一般的に使用される統計を適用することによってモデルの品質を評価する方法を学習します。
他の回帰関数と同様に、全体的なモデル品質を評価するためによく使用される統計があります。エキスパート・ユーザーは、モデル構築プロセスによって最適化するための基準として、これらの性能指数の1つを指定することもできます。モデル固有のデフォルト値を使用できるため、最適化基準の選択は必須ではありません。
13.3.1 条件付き対数尤度
対数尤度は、モデルのパラメータ値に依存する予測の確率推定値を提供するモデルの最適化基準としてよく使用される性能指数です。
モデルの確率は、トレーニング・データの実際の値に対して推定してから、パラメータ値の尤度の推定値をもたらします。観測されたターゲット値に対して高い確率をもたらすパラメータ値は、高い尤度を持つので、適切なモデルを示します。対数尤度の計算は、モデルの形式によって異なります。
条件付き対数尤度は、パラメータを2つのグループに分割します。一方のグループは正しいものとみなされ、他方のグループは誤差の発生源とみなされます。条件付き対数尤度は、前者のグループに条件付けられた後者のグループの対数尤度です。たとえば、指数平滑法(ESM)モデルは、初期モデル状態を推定します。ESMモデルの条件付き対数尤度は、その初期モデル状態(正確であると想定)が条件となっています。ESM条件付き対数尤度は次のとおりです。
ここで、etは時間tでの誤差であり、k(x(t-1) )は、加算誤差を持つESMモデルの場合は1であり、乗算誤差を持つモデルでは以前の時間ステップでの推定レベルです。
13.3.2 平均二乗誤差(MSE)とその他の誤差の測定
最適化基準としても使用できるもう1つの時系列の性能指数に、平均二乗誤差(MSE)があります。
平均二乗誤差は次のように計算されます。
ノート:
これらの「予測」は、すでに観測された期間に対するものであり、入力される時系列の一部です。時系列モデルは、先行する複数のステップごとに予測できるため、そのような予測に関連する誤差を時系列で測定できます。もう1つの性能指数である平均二乗誤差の平均値(AMSE)では、まさにそのことが行われます。入力された時系列の各期間について、多ステップ予測を計算し、それらの予測の誤差を計算して、誤差の平均を取ります。AMSEは、MSEが誤差タイプ(加算または乗算)を認識するのと同じように、個々のエラーを正確に計算します。ステップ数kは、ユーザーによって決定されます(デフォルトは3)。式は次のとおりです。
MSEのその他の性能指標には、MSEの平方根である残差標準誤差(RMSE)と、誤差の絶対値の平均である平均絶対誤差(MAE)があります。
13.3.3 不規則な時系列
不規則な時系列とは、観測値間の時間間隔が等間隔でない時系列データです。
一般的な方法の1つのは、隣接するステップ間の時間間隔を等間隔にすることです。しかし、このような間隔を時系列に強制することは、必ずしも適切または現実的ではありません。不規則な時系列では、時系列が等間隔であると仮定するのではなく、ケースIDの日付と時間の値を使用して観測値の間隔を計算します。モデルは、観測された間隔で、観測値に直接構築されます。Oracleの時系列分析では、不規則な時系列が処理されます。
13.3.4 構築および適用
新しいデータが到着すると、新しい時系列モデルが構築されます。
Oracle Machine Learning for SQLの多くの機能は、作成した1つのモデルをいくつもの異なる入力データセットに適用できるように、構築および適用の操作がそれぞれに異なります。ただし、時系列の入力はターゲット値の履歴のみで構成されます。したがって、適切な入力データのセットは1つのみとなります。新しいデータが到着したら、新しいモデルを構築するようにすることをお薦めします。モデルは一度きりの使用を想定しているため、モデルの統計値と予測値はモデルの作成時に生成され、モデル・ビューを通じて確認できます。