注: | この項では、Box-Jenkins ARIMA手法に含まれない非季節性および季節性時系列予測手法について説明します。これらの手法の詳細は、ARIMA時系列予測手法の使用を参照してください。 |
実測データは、様々な時系列予測手法を使用して予測できます。一部の手法は、特定のデータ・タイプで最適になるよう設計されています:
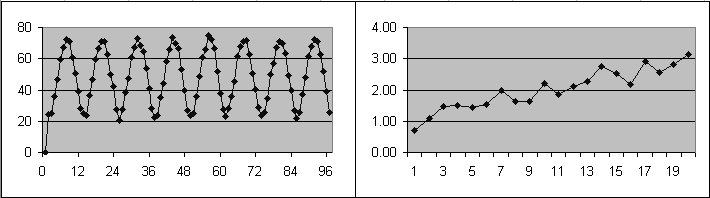
季節性データ(時間の経過で定期的に繰り返すパターンで増減; 図3.4「季節性データ(左)および傾向のあるデータ(右)」、左側)
傾向データ(時間の経過で連続して増減; 図3.4「季節性データ(左)および傾向のあるデータ(右)」、右側)
傾向または季節性のないデータ
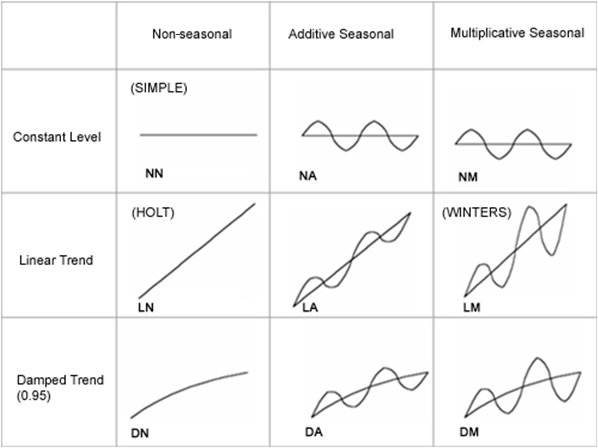
これらのカテゴリの他に、加法型および積乗型の2つのタイプの季節性手法があります。加法型季節性には、一定のパターン振幅があり、積乗型季節性には時間の経過で増加するパターン振幅があります。減衰傾向手法は非季節性または季節性にすることができ、時間の経過で減衰を表示できます。
図3.5「様々な手法曲線」は、非季節性および季節性の様々な曲線を示します。
時系列予測について、それぞれのクラシック時系列予測手法で役立つ機能は異なります。ただし、表3.1「クラシック時系列予測手法の選択」とその後の要約の段落にあるとおり、それぞれの手法には独自の目的があります。それぞれのクラシック手法の詳細は、Oracle Crystal Ballリファレンスおよびサンプル・ガイドのPredictorに関する項を参照してください。
表3.1 クラシック時系列予測手法の選択
|
傾向または季節性なし |
傾向のみ、季節性なし |
季節性のみ、傾向なし |
傾向および季節性あり |
|---|---|---|---|
|
シングル指数平滑法 |
ダブル指数平滑法 |
加法型季節 |
Holt-Wintersの加法型 |
|
シングル移動平均法 |
ダブル移動平均法 |
積乗型季節 |
Holt-Wintersの積乗型 |
|
減衰傾向平滑化 |
減衰傾向加法型 | ||
|
減衰傾向積乗型 |
[D]
選択のガイドラインを要約するには:
移動平均法 - これらの手法では、短期の変動を平滑化したり、長期の傾向または循環を強調できます。これは時系列に傾向がない場合に使用されます。時系列に傾向がある場合、ダブル移動平均法を使用して、元の移動平均から2番目の移動平均が計算され、傾向をより正確に追跡できます。
指数平滑法 - 移動平均では、包含された値に均等に重み付けしますが、シングル指数平滑法では、より合理的な方法として、観測値が古くなると指数関数的に減少するよう重み付けます。時系列に傾向がある場合は、ダブル指数平滑法が適しており、系列を2回平滑化して計算します。
減衰傾向手法 - 曲線が時間の経過でフラット化(減速)になる場合に使用します。
傾向または季節性データがあるかどうかを判定するには、「入力データ」パネルで「季節性を表示」をクリックします。詳細は、季節性による実測データの表示を参照してください。
ヒント: | 季節性を表示すると、どの手法を選択するかを決定できます。ただし、「非季節性手法」または「季節性手法」で使用可能なすべてのクラシック時系列予測手法を選択しても、数千の値を一括して予測していないかぎり計算速度が大幅に低下することはないため、すべてを選択することをお薦めします(デフォルト)。 |
予測手法選択の手順は、予測手法の選択を参照してください。
手法のパラメータを手動で設定するには、クラシック時系列予測手法パラメータの設定を参照してください。