2.2 IEEE 形式
このセクションでは、浮動小数点データがメモリー内にどのように格納されるかについて説明します。ここでは、IEEE のさまざまな格納形式の精度と範囲の要約を示します。
2.2.1 格納形式
浮動小数点形式は、浮動小数点数値を構成する各フィールド、これらのフィールドのレイアウト、およびその演算の解釈を指定するデータ構造です。浮動小数点の格納形式は、浮動小数点形式がメモリー内にどのように格納されるかを指定します。IEEE 規格は形式を定義しますが、それらの格納形式の選択は実装者に任されています。
アセンブリ言語のソフトウェアは、これらの格納形式の使用に依存している場合もありますが、より高水準な言語は通常、浮動小数点データ型の言語上の概念のみを扱います。 これらの 型は高水準言語ごとに異なる名前を持ち、表 1 に示すように IEEE 形式に対応しています。
|
IEEE 754 は、単精度と倍精度の浮動小数点形式を正確に指定し、これらの 2 つの各基本形式に対して拡張形式のクラスを定義しています。表 1 に示されている long double および REAL*16 型は、IEEE 規格で定義されている拡張倍精度形式のクラスの 1 つを示しています。
以降のセクションでは、SPARC および x86 プラットフォーム上の IEEE 浮動小数点形式に使用される各格納形式について詳細に説明します。
2.2.2 単精度形式
IEEE 単精度形式は、23 ビットの小数部 f、8 ビットのバイアス付き指数 e、および 1 ビットの符号 s の 3 つのフィールドで構成されています。 これらのフィールドは、次の図に示すように、1 つの 32 ビットワードに連続して格納されます。ビット 0:22 には 23 ビットの小数部 f が含まれ (ビット 0 が小数部の最下位ビット、ビット 22 が最上位ビット)、ビット 23:30 には 8 ビットのバイアス付き指数 e が含まれ (ビット 23 がバイアス付き指数の最下位ビット、ビット 30 が最上位ビット)、最上位ビット 31 には符号ビット s が含まれています。
図 1 単精度格納形式

表 2 は、一方にある 3 つの構成フィールド s、e、および f の値と、もう一方にある単精度形式のビットパターンによって表される値の間の対応関係を示しています。u は、示されているフィールドの値が、単精度形式の特定のビットパターンの値の決定には関係しないことを示しています。
|
e < 255 の場合、単精度形式のビットパターンに割り当てられる値は、小数部の最上位ビットのすぐ左側に 2 進基数点を挿入し、2 進小数点のすぐ左側に暗黙ビットを挿入することによって形成されます。それにより、混在した数値 (整数と小数部。ここで、0 ≤ 小数部 < 1) が 2 進定位置表記で表されます。
このように形成された混在した数値は、単精度形式の仮数と呼ばれます。暗黙ビットにこの名前が付けられているのは、その値が単精度形式のビットパターンでは明示的に指定されておらず、バイアス付き指数フィールドの値によって暗に示されているためです。
単精度形式の場合、正規数と非正規数の違いは、正規数の仮数の先行ビット (2 進小数点の左側のビット) が 1 であるのに対して、非正規数の仮数の先行ビットは 0 である点です。単精度形式の非正規数は、IEEE 規格 754 では単精度形式の非正規化数という名前になりました。
23 ビットの小数部が暗黙的先行仮数ビットと組み合わされて、単精度形式の正規数の 24 ビットの精度が実現されます。
単精度格納形式での重要なビットパターンの例を表 3 に示します。最大の正の正規数は、IEEE 単精度形式で表すことができる最大の有限数です。 最小の正の非正規数は、IEEE 単精度形式で表すことができる最小の正の数値です。最小の正の正規数は多くの場合、アンダーフローしきい値と呼ばれます。 (最大と最小の正規数および非正規数に対する 10 進数値は近似値であり、示されている桁数に関して正確です。)
|
NaN (非数) は、NaN の定義を満足させる多くのビットパターンのいずれかで表すことができます。表 3 に示されている NaN の 16 進数値は、NaN を表すために使用できる多くのビットパターンの 1 つにすぎません。
2.2.3 倍精度形式
IEEE 倍精度形式は、52 ビットの小数部 f、11 ビットのバイアス付き指数 e、および 1 ビットの符号 s の 3 つのフィールドで構成されています。 これらのフィールドは、次の図に示すように、アドレスが連続した 2 つの 32 ビットワードに連続して格納されます。
SPARC アーキテクチャーでは、上位アドレスの 32 ビットワードに小数部の最下位 32 ビットが含まれるのに対して、x86 アーキテクチャーでは、下位アドレスの 32 ビットワードに小数部の最下位 32 ビットが含まれます。
f[31:0] が小数部の最下位 32 ビットを示している場合は、ビット 0 が小数部全体の最下位ビットであり、ビット 31 は小数部の最下位 32 ビットの最上位ビットです。
もう一方の 32 ビットワードでは、ビット 0:19 には小数部の最上位 20 ビット f[51:32] が含まれ (ビット 0 がこれらの小数部の最上位 20 ビットの最下位ビット、ビット 19 が小数部全体の最上位ビット)、ビット 20:30 には 11 ビットのバイアス付き指数 e が含まれ (ビット 20 がバイアス付き指数の最下位ビット、ビット 30 が最上位ビット)、最上位ビット 31 には符号ビット s が含まれています。
次の図では、2 つの連続した 32 ビットワードが 1 つの 64 ビットワードであるかのように各ビットに番号を付けています。そこでは、ビット 0:51 に 52 ビットの小数部 f が格納され、ビット 52:62 に 11 ビットのバイアス付き指数 e が格納され、ビット 63 に符号ビット s が格納されています。
図 2 倍精度格納形式

これらの 3 つのフィールド内のビットパターンの値によって、ビットパターン全体で表される値が決定されます。
表 4 は、一方にある 3 つの構成フィールド内のビットの値と、もう一方にある倍精度形式のビットパターンによって表される値の間の対応関係を示しています。u は、示されているフィールドの値が、倍精度形式の特定のビットパターンの値の決定には関係しないことを示しています。
|
e < 2047 の場合、倍精度形式のビットパターンに割り当てられる値は、小数部の最上位ビットのすぐ左側に 2 進基数点を挿入し、2 進小数点のすぐ左側に暗黙ビットを挿入することによって形成されます。このように形成された数値は、仮数と呼ばれます。暗黙ビットにこの名前が付けられているのは、その値が倍精度形式のビットパターンでは明示的に指定されておらず、バイアス付き指数フィールドの値によって暗に示されているためです。
倍精度形式の場合、正規数と非正規数の違いは、正規数の仮数の先行ビット (2 進小数点の左側のビット) が 1 であるのに対して、非正規数の仮数の先行ビットは 0 である点です。 倍精度形式の非正規数は、IEEE 規格 754 では倍精度形式の非正規化数という名前になりました。
52 ビットの小数部が暗黙的先行仮数ビットと組み合わされて、倍精度形式の正規数の 53 ビットの精度が実現されます。
倍精度格納形式での重要なビットパターンの例を 表 5 に示します。2 番目の列のビットパターンは、2 つの 8 桁 16 進数として示されています。SPARC アーキテクチャーでは、左側が下位アドレスの 32 ビットワードの値であり、右側が上位アドレスの 32 ビットワードの値であるのに対して、x86 アーキテクチャーでは、左側は上位アドレスのワードであり、右側は下位アドレスのワードです。最大の正の正規数は、IEEE 倍精度形式で表すことができる最大の有限数です。最小の正の非正規数は、IEEE 倍精度形式で表すことができる最小の正の数値です。最小の正の正規数は多くの場合、アンダーフローしきい値と呼ばれます。(最大と最小の正規数および非正規数に対する 10 進数値は近似値であり、示されている桁数に関して正確です。)
|
NaN (非数) は、NaN の定義を満足させる多くのビットパターンのいずれかで表すことができます。表 5 に示されている NaN の 16 進数値は、NaN を表すために使用できる多くのビットパターンの 1 つにすぎません。
2.2.4 4 倍精度形式
浮動小数点環境の 4 倍精度形式もまた、拡張倍精度形式の IEEE 定義に準拠しています。 この形式は、x86 用の Oracle Developer Studio C/C++ コンパイラには存在しません。4 倍精度形式は 4 つの 32 ビットワードを占有し、112 ビットの小数部 f、15 ビットのバイアス付き指数 e、および 1 ビットの符号 s の 3 つのフィールドで構成されています。これらは、次の図に示すように連続して格納されます。
最上位アドレスの 32 ビットワードには、f[31:0] で示される小数部の最下位 32 ビットが含まれています。次の 2 つの 32 ビットワードには、それぞれ f[63:32] と f[95:64] が含まれています。次のワードのビット 0:15 には、小数部の最上位 16 ビット f[111:96] が含まれています (ビット 0 がこれらの 16 ビットの最下位ビット、ビット 15 が小数部全体の最上位ビット)。ビット 16:30 には 15 ビットのバイアス付き指数 e が含まれ (ビット 16 がバイアス付き指数の最下位ビット、ビット 30 が最上位ビット)、ビット 31 には符号ビット s が含まれています。
次の図では、4 つの連続した 32 ビットワードが 1 つの 128 ビットワードであるかのように各ビットに番号を付けています。そこでは、ビット 0:111 に小数部 f が格納され、ビット 112:126 に 15 ビットのバイアス付き指数 e が格納され、ビット 127 に符号ビット s が格納されています。
図 3 4 倍精度形式

3 つのフィールド f、e、および s 内のビットパターンの値によって、ビットパターン全体で表される値が決定されます。
表 6 は、3 つの構成フィールドの値と、4 倍精度形式のビットパターンによって表される値の間の対応関係を示しています。u は、示されているフィールドの値が特定のビットパターンの値の決定には関係しないため、考慮が必要ないものです。
|
4 倍精度の拡張倍精度格納形式での重要なビットパターンの例を表 7 に示します。2 番目の列のビットパターンは、4 つの 8 桁 16 進数として示されています。いちばん左の数値は最下位アドレスの 32 ビットワードの値であり、いちばん右の数値は最上位アドレスの 32 ビットワードの値です。最大の正の正規数は、4 倍精度形式で表すことができる最大の有限数です。最小の正の非正規数は、4 倍精度形式で表すことができる最小の正の数値です。最小の正の正規数は多くの場合、アンダーフローしきい値と呼ばれます。(最大と最小の正規数および非正規数に対する 10 進数値は近似値であり、示されている桁数に関して正確です。)
|
表 7 に示されている NaN の 16 進数値は、NaN を表すために使用できる多くのビットパターンの 1 つにすぎません。
2.2.5 拡張倍精度形式 (x86)
この浮動小数点環境の拡張倍精度形式は、拡張倍精度形式の IEEE 定義に準拠しています。 これは、63 ビットの小数部 f、1 ビットの明示的先行仮数ビット j、15 ビットのバイアス付き指数 e、および 1 ビットの符号 s の 4 つのフィールドで構成されています。 この形式は、SPARC 用の Oracle Developer Studio Fortran または C/C++ の言語の型としては使用できません。
x86 アーキテクチャーファミリでは、これらのフィールドは、アドレスが連続した 10 個の 8 ビットバイトに連続して格納されます。ただし、UNIX System V Application Binary Interface Intel 386 Processor Supplement (Intel ABI) では、次の図に示すように、拡張倍精度のパラメータや結果がスタック内でアドレスが連続した 3 つの 32 ビットワード (最上位アドレスのワードの最上位 16 ビットは未使用) を占有する必要があります。
最下位アドレスの 32 ビットワードには、小数部 f[31:0] の最下位 32 ビットが含まれています (ビット 0 が小数部全体の最下位ビット、ビット 31 が小数部の最下位 32 ビットの最上位ビット)。中央のアドレスの 32 ビットワードでは、ビット 0:30 には小数部の最上位 31 ビット f[62:32] が含まれ (ビット 0 がこれらの小数部の最上位 31 ビットの最下位ビット、ビット 30 が小数部全体の最上位ビット)、この中央のアドレスの 32 ビットワードのビット 31 には明示的先行仮数ビット j が含まれています。
最上位アドレスの 32 ビットワードでは、ビット 0:14 には 15 ビットのバイアス付き指数 e が含まれ (ビット 0 がバイアス付き指数の最下位ビット、ビット 14 が最上位ビット)、ビット 15 には符号ビット s が含まれています。 この最上位アドレスの 32 ビットワードの最上位 16 ビットは x86 アーキテクチャーファミリでは未使用ですが、上で示したように、それらの存在は Intel ABI への準拠のために不可欠です。
次の図では、3 つの連続した 32 ビットワードが 1 つの 96 ビットワードであるかのように各ビットに番号を付けています。そこでは、ビット 0:62 に 63 ビットの小数部 f が格納され、ビット 63 に明示的先行仮数ビット j が格納され、ビット 64:78 に 15 ビットのバイアス付き指数 e が格納され、ビット 79 に符号ビット s が格納されています。
図 4 拡張倍精度形式 (x86)

4 つのフィールド f、j、e、および s 内のビットパターンの値によって、ビットパターン全体で表される値が決定されます。
表 8 は、4 つの構成フィールドの 16 進数表現と、各ビットパターンによって表される値の間の対応関係を示しています。u は、示されているフィールドの値が特定のビットパターンの値の決定には関係しないことを示しています。
|
拡張倍精度形式のビットパターンには暗黙的先行仮数ビットが含まれていないことに注意してください。拡張倍精度形式では、先行仮数ビットは個別のフィールド j として明示的に指定されます。ただし、e≠ 0 の場合、j = 0 を含むビットパターンはすべて、このようなビットパターンを浮動小数点演算のオペランドとして使用すると無効な演算の例外が発生するという意味でサポートされていません。
拡張倍精度形式内の互いに素なフィールド j と f の和集合は、仮数と呼ばれます。e < 32767 かつ j = 1 の場合、または e = 0 かつ j = 0 の場合、この仮数は、先行仮数ビット j と小数部の最上位ビットの間に 2 進基数点を挿入することによって形成されます。
x86 拡張倍精度形式では、先行仮数ビット j が 0 で、かつバイアス付き指数フィールド e も 0 であるビットパターンが非正規数を表すのに対して、先行仮数ビット j が 1 で、かつバイアス付き指数フィールド e が 0 以外であるビットパターンは正規数を表します。先行仮数ビットは指数の値から推測されるのではなく、明示的に表されるため、この形式では (非正規数のように) バイアス付き指数は 0 だが、先行仮数ビットが 1 であるビットパターンも認められます。このような各ビットパターンは、実際にはバイアス付き指数フィールドが 1 である対応するビットパターン (つまり、正規数) と同じ値を表すため、これらのビットパターンは擬似非正規数と呼ばれます。非正規数は、IEEE 規格 754-1985 では非正規化数という名前になりました。擬似非正規数は単に、x86 拡張倍精度形式のエンコーディングのアーティファクトです。オペランドとして現れると対応する正規数に暗黙的に変換され、結果として生成されることはありません。
|
拡張倍精度格納形式の重要なビットパターンの例が前の表に示されています。2 番目の列のビットパターンは、1 つの 4 桁 16 進数と、それに続く 2 つの 8 桁 16 進数として示されています。前者は、最上位アドレスの 32 ビットワードの最下位 16 ビットの値です (この最上位アドレスの 32 ビットワードの最上位 16 ビットは未使用であるため、それらの値は示されていません)。後者は、左側が中央のアドレスの 32 ビットワードの値であり、右側が最下位アドレスの 32 ビットワードの値です。最大の正の正規数は、x86 拡張倍精度形式で表すことができる最大の有限数です。最小の正の非正規数は、拡張倍精度形式で表すことができる最小の正の数値です。最小の正の正規数は多くの場合、アンダーフローしきい値と呼ばれます。最大と最小の正規数および非正規数に対する 10 進数値は近似値であり、示されている桁数に関して正確です。
NaN (非数) は、NaN の定義を満足させる多くのビットパターンのいずれかで表すことができます。前の表に示されている NaN の 16 進数値は、小数部フィールドの先行 (最上位) ビットによって、NaN がシグナルを発生しない NaN (先行小数ビット = 1) またはシグナルを発生する NaN (先行小数ビット = 0) のどちらであるかが決定されることを示しています。
2.2.6 10 進数表現の範囲と精度
このセクションでは、特定の格納形式での範囲と精度の概念について説明します。ここでは、IEEE の単精度、倍精度、4 倍精度の各形式、および x86 アーキテクチャー上での IEEE 拡張倍精度形式の実装に対応する範囲と精度について説明します。範囲と精度の概念を定義する場合の具体的な例については、IEEE 単精度形式を参照してください。
IEEE 規格では、単精度形式の浮動小数点数を表すために 32 ビットを使用することが規定されています。32 個の 0 と 1 の組み合わせは有限数しか存在しないため、32 ビットでは有限数の数値しか表すことができません。
この特定の形式で表すことができる最大と最小の正の数値の 10 進数表現は何かと尋ねるのは自然なことです。
範囲の概念を導入すると、その質問を言い換えて、代わりに IEEE 単精度形式で表すことができる数値の範囲 (10 進数表記) は何かと尋ねることができます。
IEEE 単精度形式の正確な定義を考慮に入れ、正の正規化数に限定すると、IEEE 単精度形式で表すことができる浮動小数点数の範囲は次のようになると証明できます。
1.175...× (10-38) から 3.402... ×(10+38) まで
2 番目の質問は、特定の形式で表される数値の精度に関するものです。 これらの概念は、いくつかの状況と例を調べることによって説明できます。
2 進浮動小数点演算のための IEEE 規格では、単精度形式で表すことができる数値のセットが規定されています。この数値のセットは、2 進浮動小数点数のセットとして説明されます。IEEE 単精度形式の仮数は 23 ビットあり、これが暗黙的先行ビットとともに 24 桁 (ビット) の (2 進数の) 精度を生み出します。
次の数値 (10 進数の仮数 q 桁で表現できます) を 数直線 上にマークすることによって、異なる数値のセットが取得されます。
x = (x1.x2 x3...xq) × (10n)
次の図は、この状況を示しています。
図 5 デジタル表現と 2 進数表現で定義される数値のセットの比較
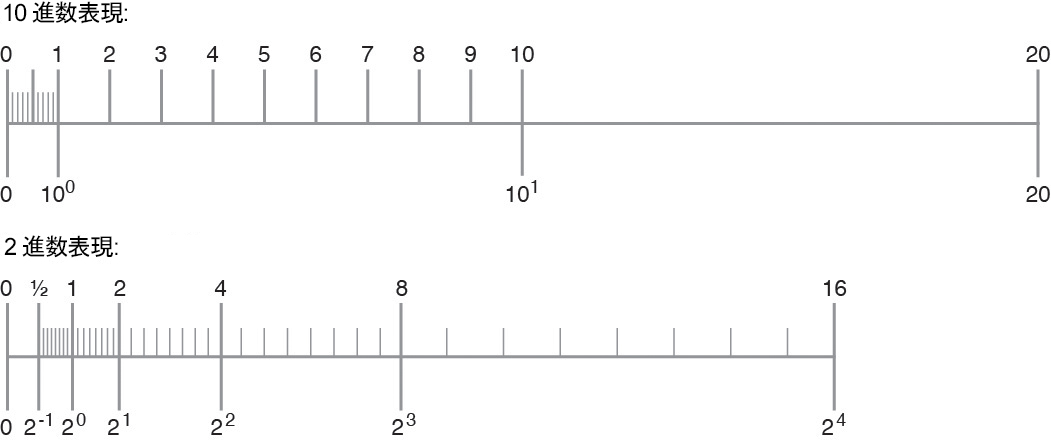
この 2 つのセットは異なることに注意してください。そのため、2 進数の有効桁数 24 桁に対応する 10 進数の有効桁数を推定するには、問題を再公式化する必要があります。
2 進数表現 (コンピュータによって使用される内部形式) と 10 進数形式 (ユーザーが通常関心を持つ形式) の間で浮動小数点数を変換するという観点から問題を再公式化します。実際に、10 進数から 2 進数に変換したあと 10 進数に戻したり、2 進数から 10 進数に変換したあと 2 進数に戻したりすることがあります。
数値のセットが異なるため、変換は一般に不正確である点に注意することが重要です。正しく実行された場合、あるセット内の数値からもう一方のセット内の数値への変換では、2 番目のセットから 2 つの隣接する数値のうちの 1 つが選択されます (具体的にどちらを選択するかは丸めに関連した問題です)。
いくつかの例を考察します。IEEE 単精度形式の次の 10 進数表現で数値を表そうとしているとします。
x = x1.x2 x3... × 10n
IEEE 単精度形式で正確に表すことができる実数は有限数しか存在せず、またその中に上の形式のすべての数値が含まれているわけではないため、一般に、このような数値を正確に表すことは不可能です。たとえば、
y = 838861.2, z = 1.3
として、次の Fortran プログラムを実行します。
REAL Y, Z
Y = 838861.2
Z = 1.3
WRITE(*,40) Y
40 FORMAT("y: ",1PE18.11)
WRITE(*,50) Z
50 FORMAT("z: ",1PE18.11)
このプログラムからの出力は、次のようになるはずです。
y: 8.38861187500E+05 z: 1.29999995232E+00
y に割り当てられた値 8.388612 × 105 と出力された値の差は 0.000000125 です。これは、y より 10 進数の 7 桁小さい値です。y を IEEE 単精度形式で表したときの正確性は、有効桁数が約 6 から 7 です。あるいは、y は、IEEE 単精度形式で表された場合、有効桁数が約 6 です。
同様に、z に割り当てられた値 1.3 と出力された値の差は 0.00000004768 です。これは、z より 10 進数の 8 桁小さい値です。z を IEEE 単精度形式で表したときの正確性は、有効桁数が約 7 から 8 です。あるいは、z は、IEEE 単精度形式で表された場合、有効桁数が約 7 です。
10 進数の浮動小数点数 a を IEEE 単精度形式の 2 進数表現 b に変換したあと、b を 10 進数 c に戻すとします。a と a - c の間には何桁あるでしょうか。
この質問を次のように言い換えます。
IEEE 単精度形式表現の a の 10 進数の有効桁数は何桁でしょうか。あるいは、x を IEEE 単精度形式で表したとき、正確であるとして信頼できる 10 進数の桁数は何桁でしょうか。
10 進数の有効桁数は常に 6 から 9 まで (つまり、少なくとも 6 桁) であり、9 桁を超えて正確であることはありません (変換が正確である場合、つまり無限数の桁を正確にできる場合を除く)。
逆に、IEEE 単精度形式の 2 進数を 10 進数に変換したあと 2 進数に戻す場合は、一般に、これらの 2 つの変換のあとに最初の数値を確実に取得できるようにするために少なくとも 10 進数 9 桁を使用する必要があります。
表 10 に全体像を示します。
|
2.2.7 Oracle Solaris 環境での基数変換
基数変換とは、ある基数で表された数値を別の基数で表された数値に変換することを指します。 C の printf、scanf や、Fortran の read、write、print などの I/O ルーチンでは、基数 2 と基数 10 で表された数値間の基数変換が必要になります。
基数 10 から基数 2 への基数変換は、従来の 10 進数表記の数値を読み込み、それを内部の 2 進数形式で格納する場合に発生します。
基数 2 から基数 10 への基数変換は、内部の 2 進数値を 10 進数の ASCII 文字列として出力する場合に発生します。
Oracle Solaris 環境では、すべての言語での基数変換のための基本的なルーチンが標準 C ライブラリ libc に含まれています。これらのルーチンは、関係する 10 進数の文字列の長さに対するわずかな制限に従って、すべての入力および出力形式間の正しく丸められた変換を生み出すテーブル駆動アルゴリズムを使用しています。テーブル駆動アルゴリズムでは、その正確性に加えて、正しく丸められた基数変換のための最悪条件での時間が削減されます。
1985 IEEE 規格では、10–44 から 10+44 までの範囲の大きさを持つ標準的な数値での正しい丸めが必要ですが、それを超える指数の場合は多少間違った丸めが許可されます。IEEE 規格 754 のセクション 5.6 を参照してください。libc のテーブル駆動アルゴリズムは、改訂された 754-2008 の要求どおり、単精度、倍精度、および拡張倍精度形式の範囲全体にわたって正しく丸めます。
C では、10 進数文字列と 2 進浮動小数点値の間の変換は、IEEE 754 に従って常に正しく丸められます。変換された結果は、現在の丸めモードによって指定された方向で元の値にもっとも近い、結果の形式で表すことができる数値です。丸めモードがもっとも近い値への丸めであり、かつ元の値が結果の形式の 2 つの表現可能な数値の間に正確に存在する場合、変換された結果は最下位の桁が偶数である方になります。これらの規則は、コンパイラによって実行されるソースコード内の定数の変換や、標準のライブラリルーチンを使用してプログラムによって実行されるデータの変換に適用されます。
Fortran では、デフォルトでは、10 進数文字列と 2 進浮動小数点値の間の変換は C と同じ規則に従って正しく丸められます。I/O 変換の場合、もっとも近い値への丸めモードの「偶数に結び付ける丸め」の規則は、プログラムで ROUNDING= 指定子を使用するか、または –iorounding フラグでコンパイルすることによってオーバーライドできます。詳細は、Oracle Developer Studio 12.5: Fortran ユーザーズガイドおよび f95(1) のマニュアルページを参照してください。
基数変換に関するリファレンス (特に Coonen 氏の論文や Sterbenz 氏の書籍) については、参考資料 を参照してください。