2.3 アンダーフロー
アンダーフローは、大まかに述べると、算術演算の結果が小さすぎるために、その目的の宛先形式に格納しようとすると通常より大きい丸め誤差を必ず引き起こしてしまう場合に発生します。
2.3.1 アンダーフローしきい値
表 11 は、 単精度、倍精度、および拡張倍精度でのアンダーフローしきい値を示しています。
| |||||||||||||||
正の非正規数は、最小の正規数と 0 の間にある数値です。 最小の正規数に近い 2 つの (正の) 非常に小さい数値を引くと、非正規数が生成される可能性があります。または、最小の正の正規数を 2 で割ると、非正規数の結果が生成されます。
非正規数の存在によって、小さい数値が関係する浮動小数点演算により高い精度が提供されますが、非正規数自体の精度のビット数は正規数より少なくなります。数学的に正しい結果が最小の正の正規数より小さい大きさを持つときに (0 の答えを返すのではなく) 非正規数を生成する方法は、段階的アンダーフローと呼ばれます。
このようなアンダーフローの結果を処理するための方法は、ほかにもいくつかあります。以前は一般的であった 1 つの方法として、これらの結果を 0 にフラッシュする方法があります。 この方法は突発的アンダーフローと呼ばれ、IEEE 規格が現れる前はほとんどのメインフレーム上でデフォルトでした。
IEEE 規格 754 の草案を作成した数学者やコンピュータ設計者は、数学的に堅牢な解決方法への望みと、効率的に実装できる標準を作成する必要性のバランスをとりながら、いくつかの代替方法を検討しました。
2.3.2 IEEE 演算でのアンダーフローの処理方法
IEEE 規格 754 では、アンダーフローの結果を処理するための望ましい方法として段階的アンダーフローが選択されています。この方法では、格納された値のための 2 つの表現として、正規と非正規を定義します。
正規の浮動小数点数の IEEE 形式は、次のように示されます。
(-1)s × (2(e–bias)) × 1.f
ここで、s は符号ビット、e はバイアス付き指数、f は小数部です。数値を完全に指定するために格納する必要があるのは、s、e、および f だけです。仮数の暗黙的先行ビットは正規数では 1 であると定義されているため、格納する必要はありません。
そのため、格納できる最小の正の正規数は、最大の大きさの負の指数とすべてが 0 の小数部を持っています。先行ビットを 1 ではなく 0 であると見なすことによって、さらに小さい数値にも対応できます。倍精度形式では、小数部の長さが 52 ビット (10 進数では約 16 桁) であるため、これによって最小の指数が 10‐308 から実質的に 10‐324 に拡張されます。これらが非正規数であり、アンダーフローした結果を 0 にフラッシュするのではなく、非正規数を返す方法が段階的アンダーフローです。
明らかに、非正規数が小さくなるほど、その小数部に含まれる 0 以外のビットは少なくなります。非正規数の結果を生成する計算には、相対的な丸め誤差に関して、正規数のオペランドに対する計算と同じ制限は適用されません。ただし、段階的アンダーフローに関して重要な点は、その使用によって次のことが暗黙的に示されることです。
非正規の浮動小数点数の IEEE 形式は、次のように示されます。
(-1)s × (2(-bias+1)) × 0.f
ここで、s は符号ビット、バイアス付き指数 e は 0、f は小数部です。暗黙的な 2 のべき乗のバイアスが正規数の形式でのバイアスより 1 大きく、小数部の暗黙的先行ビットが 0 であることに注意してください。
段階的アンダーフローを使用すると、表現可能な数値の小さい方の範囲を拡張できます。ある値を疑わしくするのは小ささではなく、それに関連する誤差です。非正規数を活用するアルゴリズムでは、誤差制限がほかのシステムより小さくなります。次のセクションでは、段階的アンダーフローに対する数学的なある程度の正当化を示します。
2.3.3 段階的アンダーフローを使用する理由
非正規数の目的は、ほかの一部の演算モデルとは異なり、アンダーフローやオーバーフローを完全に回避することではありません。代わりに、非正規数は、さまざまな計算 (通常、乗算のあとの加算) での問題の原因としてのアンダーフローを排除します。詳細は、James Demmel 著『Underflow and the Reliability of Numerical Software』および S. Linnainmaa 著『Combating the Effects of Underflow and Overflow in Determining Real Roots of Polynomials』を参照してください。
演算に非正規数が存在するため、以降の加算や減算で、正確性の損失を招きかねない、トラップされないアンダーフローが発生することはなくなります。x と y が 2 倍以内に収まっている場合は、x – y で誤差は発生しません。これは、アルゴリズム内の重要な場所で、有効な精度を実質的に高くしている多くのアルゴリズムにとって重要な点です。
さらに、段階的アンダーフローでは、アンダーフローによる誤差が通常の丸め誤差より悪化することはありません。これは、アンダーフローを処理するためのほかのどのような方法に関して行われるよりはるかに強い表明であり、この点が段階的アンダーフローに対するもっとも適切な正当化の 1 つです。
2.3.4 段階的アンダーフローの誤差の属性
計算された結果 = 正しい結果 + 丸め
丸めがどれだけ大きくなる場合があるかを示す便利な尺度の 1 つとして、最終桁単位 (「unit in the last place」を略して ulp) と呼ばれるものがあります。浮動小数点数のその標準の表現における小数部の最下位ビットは、その最終桁です。このビットによって表される値 (たとえば、このビット以外は表現が同じである 2 つの数値の絶対的な違い) は、その数値の最終桁単位です。計算された結果が正しい結果をもっとも近い表現可能な数値に丸めることによって取得された場合は、明らかに、丸め誤差が計算された結果の最終桁単位の半分より大きくなることはありません。言い換えると、もっとも近い値への丸めモードの IEEE 演算では、次の計算結果になります。
0 ≤ |丸め| ≤½ulp
ulp が相対的な量であることに注意してください。非常に大きな数値の ulp はそれ自体が非常に大きいのに対して、非常に小さい数値の ulp はそれ自体が非常に小さくなります。この関係は、ulp を関数として表すことによって明示的にすることができます。ulp(x) は、浮動小数点数 x の最終桁単位を示します。
さらに、浮動小数点数の ulp は、その数値が表される精度によって異なります。たとえば、表 12 は、前に説明した 4 つの各浮動小数点形式での ulp(1) の値を示しています。
|
前に説明したように、どのコンピュータ演算でも、正確に表すことができる数値のセットは有限数しか存在しません。数値の大きさが小さくなり、0 に近づくにつれて、隣接する表現可能な数値の間隔は狭くなります。逆に、数値の大きさが大きくなるにつれて、隣接する表現可能な数値の間隔は広がります。
たとえば、3 ビットの精度しかない 2 進演算を使用しているとします。この場合は、次の図に示すように、任意の 2 つの 2 のべき乗の間には 23 = 8 個の表現可能な数値があります。
図 6 数直線
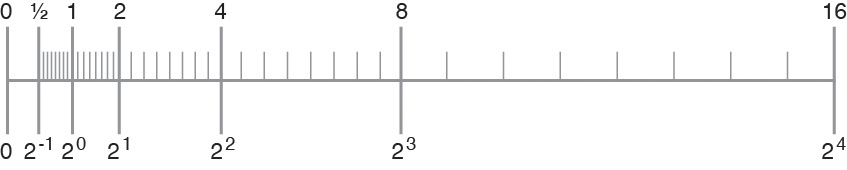
この数直線は、指数が 1 増えるごとに数値の間隔が 2 倍になる様子を示しています。
IEEE 単精度形式では、2 つの最小の正の非正規数の大きさの違いが約 10-45 であるのに対して、2 つの最大の有限数の大きさの違いは実に約 1031 もあります。
表 13 で、nextafter(x,+∞) は、数直線に沿って +∞ に向かって移動したとき、x のあとの次の表現可能な数値を示しています。
|
表現可能な浮動小数点数の従来のどのセットも、1 つの不正確な結果の最悪の影響によって、計算された結果の表現可能な近傍のいずれかとの間隔より悪化することはない誤差が導入されるという属性を備えています。表現可能なセットに非正規数が追加されたときに、段階的アンダーフローが実装されている場合は、1 つの不正確な、またはアンダーフローした結果の最悪の影響によって、計算された結果の表現可能な近傍のいずれかとの間隔を超えることはない誤差が導入されます。
特に、0 と最小の正規数の間の領域では、任意の 2 つの隣接する数値の間隔は 0 と最小の非正規数の間隔に等しくなります。 非正規数の存在によって、もっとも近い表現可能な数値との間隔を超える丸め誤差が導入される可能性が排除されます。
どの計算も、計算された結果の表現可能な近傍のいずれかとの間隔を超える丸め誤差を招くことはないため、堅牢な演算環境の多くの重要な属性が保持されます。これには、次の 3 つが含まれます。
x – y ≠ 0 の場合のみ x ≠ y
x と y のうちの大きい方の丸め誤差以内まで、(x – y) + y ≈ x
x が正規化数のとき、1/(1/x) ≈ x。つまり、最大の正規化数 x についても 1/x ≠ 0
代替のアンダーフロースキームは、アンダーフローの結果を 0 にフラッシュする突発的アンダーフローです。 突発的アンダーフローは、x – y がアンダーフローした場合は常に、最初の属性と 2 番目の属性に違反します。突発的アンダーフローはまた、1/x がアンダーフローした場合は常に、3 番目の属性にも違反します。
λが最小の正の正規化数 (アンダーフローしきい値とも呼ばれます) を表すものとします。 この場合、段階的アンダーフローと突発的アンダーフローの誤差の属性はλの観点から比較できます。
段階的アンダーフロー: |誤差| < λの ½ulp
突発的アンダーフロー: |誤差| ≈ λ
λの最終桁単位の半分とλ自体には大きな違いがあります。
2.3.5 段階的アンダーフローと突発的アンダーフローを比較した 2 つの例
次に、2 つのよく知られた数学的な例を示します。最初の例は、内積を計算するコードです。
sum = 0;
for (i = 0; i < n; i++) {
sum = sum + a[i] * y[i];
}
return sum;
段階的アンダーフローでは、結果は丸めによって許可される範囲で正確です。突発的アンダーフローでは、もっともらしく見えるが、はるかに不適切な、0 以外の小さい総計が提供される可能性があります。ただし、こうした問題を回避するために、賢いプログラマなら、数値が小さいために正確性が低下する場所を予測できる場合は計算をスケーリングするという点を認める必要があります。
複素数の商を導き出している 2 番目の例は、スケーリングには適していません。
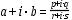|r / s|≤1 と仮定する
![image:=[ (p ?? (r / s) + q) + i(q ?? (r / s) - p) ] / [ s + r ?? (r / s) ]](figures/2-3-5-pt2.jpg "=[ (p ?? (r / s) + q) + i(q ?? (r / s) - p) ] / [ s + r ?? (r / s) ]")
.
丸めにもかかわらず、計算された複素数の結果が正確な結果と異なり、その差は p + i · q と r + i · s がそれぞれ数 ulp 程度を超えない不安定さだったとしたら正確な結果になっていた値を超えない程度であったことを示すことができます。この誤差分析は、a と b の両方がアンダーフローした場合は、誤差が |a + i · b| の数 ulp で制限される点を除き、アンダーフローが発生した場合にも保持されます。アンダーフローが 0 にフラッシュされた場合は、どちらの結論も当てはまりません。
複素数の商を計算するためのこのアルゴリズムは堅牢であり、段階的アンダーフローが存在する場合の誤差分析に適しています。突発的アンダーフローが発生した場合に複素数の商を計算するための、同様に堅牢で、分析が容易であり、かつ効率的なアルゴリズムは存在しません。突発的アンダーフローでは、低レベルの複雑な詳細事項を気にすることによる負担は、浮動小数点環境の実装者からそのユーザーに移ります。
段階的アンダーフローが存在する場合は成功するが、突発的アンダーフローでは失敗する問題のクラスは、突発的アンダーフローのユーザーが認識しているより広範囲です。次に示すような、よく使用される数値技法の多くはこのクラスに分類されます。
線形方程式の解法
多項式の解法
数値積分
収束加速法
複素数の除算
2.3.6 アンダーフローは問題か
これらの例にもかかわらず、アンダーフローはめったに問題にならないと議論される場合もあります。問題にならないなら、悩む必要がありません。しかし、この議論は堂々巡りを招くものです。
段階的アンダーフローが存在しない場合、ユーザープログラムは、暗黙的な不正確性のしきい値に敏感になる必要があります。 たとえば、単精度で計算の一部でアンダーフローが発生し、突発的アンダーフローを使用してアンダーフローした結果が 0 に置き換えられた場合は、単精度の指数での通常の低い範囲である 10-38 ではなく、約 10-31 までしか正確性を保証できません。
つまり、プログラマは、この不正確性のしきい値に近づいている時期を検出するための独自の方法を実装するか、そうでなければ自分のアルゴリズムの堅牢で、安定した実装に対する追求を諦める必要があります。
一部のアルゴリズムは、0 に近い制限された領域では計算が実行されないようにスケーリングできます。ただし、アルゴリズムのスケーリングや不正確性のしきい値の検出は、ほとんどのデータには必要がなくても、困難で、しかも時間がかかる場合があります。