4.5 Speedups

If the compiler does not parallelize a portion of a program where a significant amount of time is spent, then no speedup occurs. For example, if a loop that accounts for five percent of the execution time of a program is parallelized, then the overall speedup is limited to five percent. However, any improvement depends on the size of the workload and parallel execution overheads.

As a general rule, the larger the fraction of program execution that is parallelized, the greater the likelihood of a speedup.

Each parallel loop incurs a small overhead during startup and shutdown. The start overhead includes the cost of work distribution, and the shutdown overhead includes the cost of the barrier synchronization. If the total amount of work performed by the loop is not big enough then no speedup will occur. In fact, the loop might even slow down. If a large amount of program execution is accounted by a large number of short parallel loops, then the whole program may slow down instead of speeding up.

The compiler performs several loop transformations that try to increase the granularity of the loops. Some of these transformations are loop interchange and loop fusion. If the amount of parallelism in a program is small or is fragmented among small parallel regions, then the speedup is usually less.

Scaling up a problem size often improves the fraction of parallelism in a program. For example, consider a problem that consists of two parts: a quadratic part that is sequential, and a cubic part that is parallelizable. For this problem, the parallel part of the workload grows faster than the sequential part. At some point the problem will speed up unless it runs into resource limitations.

Try some tuning and experimentation with directives, problem sizes, and program restructuring in order to achieve the most benefit from parallel C.

4.5.1 Amdahl’s Law

Fixed problem-size speedup is generally governed by Amdahl's law, which simply says that the amount of parallel speedup of a given problem is limited by the sequential portion of the problem. The following equation describes the speedup, S, of a problem where F is the fraction of time spent in sequential code and the remaining fraction of the time (1 - F) is divided up uniformly among P processors. If the second term of the equation ((1 - F) / P) drops to zero, the total speedup is limited by the first term, F, which remains fixed.

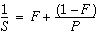
The following figure illustrates this concept diagrammatically. The darkly shaded portion represents the sequential part of the program, and remains constant for one, two, four, and eight processors. The lightly shaded portion represents the parallel portion of the program that can be divided uniformly among an arbitrary number of processors.

Figure 2  Fixed Problem Speedups

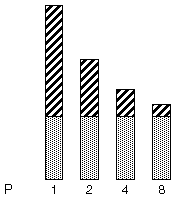
As the number of processors increases, the amount of time required for the parallel portion of each program decreases whereas the serial portion of each program stays the same.

In reality, however, you might incur overheads due to communication and distribution of work to multiple processors. These overheads might not be fixed for arbitrary numbers of processors used.

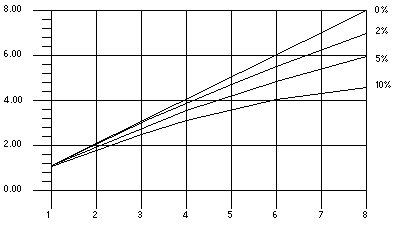
The following figure illustrates the ideal speedups for a program containing 0%, 2%, 5%, and 10% sequential portions. No overhead is assumed.

Figure 3  Amdahl's Law Speedup Curve

4.5.1.1 Overheads

Once the overheads are incorporated in the model, the speedup curves change dramatically. For the purposes of illustration, assume that overheads consist of two parts: a fixed part that is independent of the number of processors, and a non-fixed part that grows quadratically with the number of the processors used:

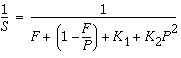
In this equation, K₁ and K₂ are some fixed factors. Under these assumptions, the speedup curve is shown in the following figure. Note that in this case, the speedups peak out. After a certain point, adding more processors is detrimental to performance.

Figure 4  Speedup Curve With Overheads

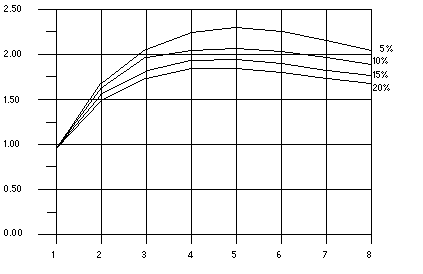
The graph shows that all programs reach the greatest speedup at five processors and then lose this benefit as up to eight processors are added. The x-axis measures the number of processors and the y-axis measures the speedup.

4.5.1.2 Gustafson’s Law

Amdahl's law can be misleading for predicting parallel speedups in real problems. The fraction of time spent in sequential sections of the program sometimes depends on the problem size. That is, by scaling the problem size, you might improve the chances of speedup, as shown in the following example.

Example 22  Scaling the Problem Size Might Improve Chances of Speedup

/*
* initialize the arrays
*/
for (i=0; i < n; i++) {
    for (j=0; j < n; j++) {
            a[i][j] = 0.0;
            b[i][j] = ...
            c[i][j] = ...
    }
}
/*
* matrix multiply
*/
for (i=0; i < n; i++) {
    for(j=0; j < n; j++) {
            for (k=0; k < n; k++) {
                a[i][j] = b[i][k]*c[k][j];
            }
    }
}

Assume an ideal overhead of zero and that only the second loop nest is executed in parallel. For small problem sizes (that is, small values of n), the sequential and parallel parts of the program are not so far from each other. However, as n grows larger, the time spent in the parallel part of the program grows faster than the time spent in the sequential part. For this problem, increasing the number of processors as the problem size increases is beneficial.