11 Recovering from Failure
Error conditions and failure situations can impact availability. If the error condition can be recovered automatically, then normal operations resume. However, there may be situations where you need to intervene to recover from failure.
TimesTen Scaleout has included error and failure detection with automatic recovery for many error and failure situations in order to maintain a continuous operation for all applications using TimesTen Scaleout. Errors and failure situations can include:
-
Software errors.
-
Network outage or other communication channel failures. A communication channel is a TCP connection.
-
One or more machines hosting a data instance unexpectedly reboots or crashes.
-
The main TimesTen daemon for an instance or any of its sub-daemons fail.
-
An element becomes slow or unresponsive either from a hang situation or as a result of a heavy load.
-
A machine or rack of machines hosting data instances are unexpectedly brought down for unknown reasons.
The response necessary for error conditions and failure situations are as follows:
-
Transient errors: A transient error is due to a temporary condition that TimesTen Scaleout is usually able to quickly resolve. You can immediately retry the failed transaction, which normally succeeds.
-
Element failure: When an element fails, TimesTen Scaleout can automatically recover the element most of the time. However, there are certain element failure situations where you may be required to fix the problem. The application response to an element failure may differ depending on the configuration of the grid and the database. After the problem is fixed, either TimesTen Scaleout recovers the element and operations continue or you supply a new element to take the place of the failed element.
-
Replica set failure: If all of the elements in a replica set fail, there is a method for TimesTen Scaleout to automatically recover the elements (once the original failure issue has been fixed). The element with the latest changes, known as the seed element, is recovered first. Then, all subsequent elements are recovered from the seed element.
-
Database failure: If all replica sets fail, the database is considered failed. You need to reload the database for recovery. How a database recovers when the database reloads depends on the value for the
Durabilityattribute. -
Data distribution failure: You can attempt a re-synchronization of your data if the data distribution process is interrupted or fails to complete. Re-synchronization involves executing the
ttGridAdmin dbDistribute -resyncoperation.
The following sections describe the error or failure situations and recovery:
-
Availability despite the failure of one element in a replica set
-
Unavailability of data when a full replica set is down or fails
Displaying the database, replica set and element status
The element status shows:
-
If the element is loaded (
opened). -
If the element is in process of a change, such as being opened (
opening), loaded (creating,loading), unloaded (unloading), destroyed (destroying) or closed (closing). -
If the element or its data instance has failed and is waiting on the seed element to recover, then the status displayed is
waiting for seed. The element that failed with the latest changes, known as the seed element, is recovered first to the latest transaction in the checkpoint and transaction log files. The other element in the replica set is copied from the seed element of the replica set. -
If the element is not up (
evictedordown).
The following examples show how to display the status of the database, data space groups, replica sets and elements. See "Troubleshooting based on element status" for details on how to respond to each status.
Example 11-1 Displaying the status of the database and all elements
You can use the ttGridAdmin dbStatus -all command to list the current status for the database, all elements, replica sets and data space groups in your database.
The first section describes the status of the overall database. In this example, the database has been created, loaded, and open. The status also shows the total number of created, loaded and open elements.
The database status shows the progression of the database being first created, then loaded and finally opened. In bringing down the database, the reverse order is performed, where the database is first closed, then unloaded and finally destroyed.
% ttGridAdmin dbStatus database1 -all Database database1 summary status as of Thu Feb 22 07:37:28 PST 2018 created,loaded-complete,open Completely created elements: 6 (of 6) Completely loaded elements: 6 (of 6) Completely created replica sets: 3 (of 3) Completely loaded replica sets: 3 (of 3) Open elements: 6 (of 6)
However, if the database status shows that the database is created, loaded and closed, then the database has not yet been opened. The following example shows that the database is not open yet, but that the distribution map has been updated, showing the created and loaded replica sets. Note that none of the elements are opened until the database is opened.
% ttGridAdmin dbStatus database1 -all Database database1 summary status as of Thu Feb 22 07:37:01 PST 2018 created,loaded-complete,closed Completely created elements: 6 (of 6) Completely loaded elements: 6 (of 6) Completely created replica sets: 3 (of 3) Completely loaded replica sets: 3 (of 3) Open elements: 0 (of 6)
The second section provides information about the elements: the host and instance name in which each element exists, the number assigned to the element, and the status of the element.
Database database1 element level status as of Thu Feb 22 07:37:28 PST 2018 Host Instance Elem Status Date/Time of Event Message ----- --------- ---- ------ ------------------- ------- host3 instance1 1 opened 2018-02-22 07:37:25 host4 instance1 2 opened 2018-02-22 07:37:25 host5 instance1 3 opened 2018-02-22 07:37:25 host6 instance1 4 opened 2018-02-22 07:37:25 host7 instance1 5 opened 2018-02-22 07:37:25 host8 instance1 6 opened 2018-02-22 07:37:25
The third section provides information about the replica sets. In this example, there are three replica sets. In addition to information about the elements, it also provides the number of the replica set in which each element exists, identified by the RS column. The data space group in which each element exists (within its data instance within its host) is identified with the DS column. Notice that each replica set has one element in each data space group.
Database database1 Replica Set status as of Thu Feb 22 07:37:28 PST 2018
RS DS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host3 instance1 opened 2018-02-22 07:37:25
2 2 host4 instance1 opened 2018-02-22 07:37:25
2 1 3 host5 instance1 opened 2018-02-22 07:37:25
2 4 host6 instance1 opened 2018-02-22 07:37:25
3 1 5 host7 instance1 opened 2018-02-22 07:37:25
2 6 host8 instance1 opened 2018-02-22 07:37:25
The final section organizes the information about the elements to show which elements are located in each data space group, shown under the DS column. In this example, there are two data space groups. The elements are organized either under data space group 1 or 2.
Database database1 Data Space Group status as of Thu Feb 22 07:37:28 PST 2018
DS RS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host3 instance1 opened 2018-02-22 07:37:25
2 3 host5 instance1 opened 2018-02-22 07:37:25
3 5 host7 instance1 opened 2018-02-22 07:37:25
2 1 2 host4 instance1 opened 2018-02-22 07:37:25
2 4 host6 instance1 opened 2018-02-22 07:37:25
3 6 host8 instance1 opened 2018-02-22 07:37:25
The following shows the status if you evicted one of your replica sets without replacement. While the database is loaded and opened, it shows that there are six created elements, but only four of those are loaded. There is one less replica set in all displayed sections and the evicted elements are shown as evicted with their status.
% ttGridAdmin dbStatus database1 -all
Database database1 summary status as of Thu Feb 22 07:52:08 PST 2018
created,loaded-complete,open
Completely created elements: 6 (of 6)
Completely loaded elements: 4 (of 6)
Completely created replica sets: 2 (of 2)
Completely loaded replica sets: 2 (of 2)
Open elements: 4 (of 6)
Database database1 element level status as of Thu Feb 22 07:52:08 PST 2018
Host Instance Elem Status Date/Time of Event Message
----- --------- ---- ------- ------------------- -------
host3 instance1 1 evicted 2018-02-22 07:52:06
host4 instance1 2 evicted 2018-02-22 07:52:06
host5 instance1 3 opened 2018-02-22 07:37:25
host6 instance1 4 opened 2018-02-22 07:37:25
host7 instance1 5 opened 2018-02-22 07:37:25
host8 instance1 6 opened 2018-02-22 07:37:25
Database database1 Replica Set status as of Thu Feb 22 07:52:08 PST 2018
RS DS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 3 host5 instance1 opened 2018-02-22 07:37:25
2 4 host6 instance1 opened 2018-02-22 07:37:25
2 1 5 host7 instance1 opened 2018-02-22 07:37:25
2 6 host8 instance1 opened 2018-02-22 07:37:25
Database database1 Data Space Group status as of Thu Feb 22 07:52:08 PST 2018
DS RS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 3 host5 instance1 opened 2018-02-22 07:37:25
2 5 host7 instance1 opened 2018-02-22 07:37:25
2 1 4 host6 instance1 opened 2018-02-22 07:37:25
2 6 host8 instance1 opened 2018-02-22 07:37:25
See "Troubleshooting based on element status" in this guide and "Database management operations" and "Monitor the status of a database (dbStatus)" in the Oracle TimesTen In-Memory Database Reference for full details on the different status options.
Recovering from transient errors
Because a grid spans multiple hosts, there is an opportunity for multiple types of failure, many of which can be transient errors. For the most part, TimesTen Scaleout can detect transient errors and adapt to them quickly. Most errors in the grid are transient with error codes designated as Transient, which may cause a specific API, SQL statement or transaction to fail. Most of the time, the application can retry the exact same operation with success.
The potential impacts of a transient error are:
-
The execution of a particular statement failed. Your application should re-execute the statement.
-
The execution of a particular transaction failed. Your application should roll back the transaction and perform the operations of the transaction again.
-
The connection to the data instance fails. If you are using a client/server connection, then the TimesTen Scaleout routes the connection to another active data instance. See "Client connection failover" for full details.
The following sections describe how TimesTen Scaleout recovers the element from the more common transient errors:
Retry transient errors
While TimesTen Scaleout automatically handles the source of most transient errors, your application may retry the entire transaction when receiving the error described in Table 11-1.
Table 11-1 SQLSTATE and ORA errors for retrying after transient failure
| SQLSTATE |
ORA errors |
PL/SQL exceptions | Error message |
|---|---|---|---|
|
|
|
Exception |
Transient transaction failure due to unavailability of a grid resource. Roll back the transaction and then retry the transaction. |
Your applications can check for the transient error as follows:
-
ODBC or JDBC applications check for the
SQLSTATE TT005error to determine if the application should retry the transaction. See "Retrying after transient errors (ODBC)" in the Oracle TimesTen In-Memory Database C Developer's Guide and "Retrying after transient errors (JDBC)" in the Oracle TimesTen In-Memory Database Java Developer's Guide for more details. -
OCI and Pro*C applications check for the
ORA-57005error to determine if the application should retry a SQL statement or transaction. See "Transient errors (OCI)" in the Oracle TimesTen In-Memory Database C Developer's Guide for more details. -
PL/SQL applications check for the
-57005PL/SQL exception to determine if the application should retry the transaction. See "Retrying after transient errors (PL/SQL)" in the Oracle TimesTen In-Memory Database PL/SQL Developer's Guide for more details.
Communications error
The following describes the type of communications that might fail:
-
Communication between elements: Used to execute SQL statements within transactions and stream data between elements, as required. If there is a communications error while the application is executing a transaction, then you must roll back the transaction. When you retry the transaction, communications are recreated and work continues.
-
Communication between data instances: The data instances communicate with each other for creating communication as well as sending or receiving recovery messages. If there is a break in the communication between the data instances, then communications are automatically recovered when you retry the operation.
-
Communication between data instances and the ZooKeeper membership servers: Each data instance communicates with the ZooKeeper membership service through one of the defined ZooKeeper servers. If communications fail between a data instance and the ZooKeeper server with which it has been communicating, then the data instance attempts to connect to another ZooKeeper server. If the data instance cannot connect to any ZooKeeper server, then the data instance considers itself to be down.
See "Recovering when a data instance is down" for details on what to do when a data instance is down.
Software error
If a software error causes an element to be unloaded, then an error is returned to the active application. After rolling back the transaction, the application can continue executing transactions as long as one element from each replica set is open.
TimesTen Scaleout attempts to reload the element. Once opened, the element can accept transactions again.
Note:
You can manually initiate the reload of an element by reloading the database with thettGridAdmin dbload command. If element status is load failed, fix what caused the element load to fail and then reload the element with the ttGridAdmin dbload command. See "Load a database into memory (dbLoad)" in the Oracle TimesTen In-Memory Database Reference for details.Host or data instance failure
If the host that contains a data instance crashes or if the data instance crashes, then an error is returned to the active application. Since the data instance is down, the element status is displayed as down. If the data instance restarts (whether from automatic recovery or manual intervention), the element within the data instance most likely recovers. Monitor the status of the element with the ttGridAdmin dbStatus command to verify if it did recover.
Note:
See "Troubleshooting based on element status" for information on how to respond to the element status. See "Recovering when a data instance is down" on how to manually recover a data instance.Heavy load or temporary communication failure
A transient failure may occur if an element becomes slow or unresponsive due to heavy load. During a database operation, a transient failure can occur for many reasons.
-
A query timeout may occur if one or more hosts of the TimesTen Scaleout are overloaded and are slow to respond.
-
A transient failure occurs with a temporary suspension of communication, such as unplugging from the network to reset communications.
Recovering from a data distribution error
Your existing data is redistributed once you apply the change to the distribution map with the ttGridAdmin dbDistribute -apply command. (See "Redistributing data in a database" for full details.) You receive an error if you request a data distribution or a reset while a data distribution is in progress.
TimesTen spawns multiple processes to perform data distribution. In addition, the active management instance communicates with the data instances to facilitate data distribution. The active management instance stores metadata to track the progress of each data distribution. Thus, the data distribution could fail if a critical process fails, an instance fails, or communication fails between the active management instance and the data instances.
The following error message displays if the dbDistribute -apply command fails during data distribution:
% ttGridAdmin dbDistribute database1 -apply Error : Distribution failed, error message lost due to process failure
There are a few failure cases where the active management instance may not know about the success or failure of a data distribution operation and the metadata may be left in an intermediate state. This could occur if the process in which the dbDistribute -apply was executed dies or is killed.
Do not re-initiate another dbDistribute -apply command if the data distribution fails or does not complete. Instead, execute the dbDistribute -resync command. The dbDistribute -resync command examines the metadata in the active management instance to determine if a dbDistribute -apply operation was in progress but did not complete (neither committing nor rolling back the changes). If so, the dbDistribute -resync command re-synchronizes the metadata in the database with the metadata in the active management instance (if they do not have matching states).
-
If the
dbDistribute -resynccommand succeeds, the re-synchronization may result in committing or rolling back the metadata changes of the previousdbDistribute -applyoperation. -
If the
dbDistribute -resynccommand fails, you can either:-
Execute the
dbDistribute -applycommand to attempt the same distribution. -
Execute the
dbDistribute -resetcommand to discard all distribution settings that have not yet been applied, then attempt a new data distribution with thedbDistribute -applycommand.
-
The following example shows the output when the dbDistribute -resync command successfully completes the data distribution operation:
% ttGridAdmin dbDistribute -resync Distribution map updated
The following example shows the output when the dbDistribute -resync command rolls back the data distribution operation:
% ttGridAdmin dbDistribute database1 -resync Distribution map Rolled Back
The following example shows the output when the dbDistribute -resync command discovers that there is no data distribution in progress.
% ttGridAdmin dbDistribute database1 -resync No DbDistribute is currently in progress
The following example shows the output when the dbDistribute -resync command discovers that the data distribution is still in progress.
% ttGridAdmin dbDistribute database1 -resync Distribute is still in progress. Wait for dbDistribute to complete, then call resync
An error displays if the re-synchronization fails. For example, you might attempt to re-synchronize a data distribution when there are no active data instances. In this case, the following error displays:
% ttGridAdmin dbDistribute database1 -resync Error : Could not connect to data instance to retrieve partition table version
See "Set or modify the distribution scheme of a database (dbDistribute)" in the Oracle TimesTen In-Memory Database Reference for more details.
Tracking the automatic recovery for an element
If an element becomes unloaded, TimesTen Scaleout attempts to reload the element if the database is supposed to be loaded. During this time, the element status changes to loading as the element is being automatically recovered by TimesTen Scaleout.
You can monitor the element status with the ttGridAdmin dbStatus -element command. This example shows that the element on the host3.instance1 data instance is in the process of recovering by showing a status of loading.
% ttGridAdmin dbStatus database1 -element Database database1 element level status as of Wed Jan 10 14:34:08 PST 2018 Host Instance Elem Status Date/Time of Event Message ----- --------- ---- ------ ------------------- ------- host3 instance1 1 loading 2018-01-10 14:33:23 host4 instance1 2 opened 2018-01-10 14:33:21 host5 instance1 3 opened 2018-01-10 14:33:23 host6 instance1 4 opened 2018-01-10 14:33:23 host7 instance1 5 opened 2018-01-10 14:33:23 host8 instance1 6 opened 2018-01-10 14:33:23
See "Availability despite the failure of one element in a replica set" and "Unavailability of data when a full replica set is down or fails" for more details on what happens when an element or a full replica set goes down.
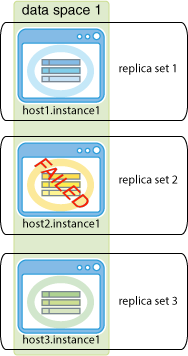
Availability despite the failure of one element in a replica set
A main goal for TimesTen Scaleout is to provide access to the data even if there are failures. When k = 2, the data contained within a replica set is available as long as at least one element in the replica set is up. If an element in the replica set goes down and then recovers, then the element is automatically re-synchronized with the other element in its replica set.
Note:
If k =1, any element failure results in the replica set being down because the replica set contains only a single element. See "Unavailability of data when a full replica set is down or fails" for details on recovery when an element permanently fails when k = 1.The following example shows a grid where k = 2. Three replica sets are created, each with two elements in the replica set. The element on the host4.instance1 data instance fails. TimesTen Scaleout automatically re-connects to the element within the host3.instance1 data instance to continue executing the transaction. While the element on the host4.instance1 data instance is unavailable or in the middle of recovering, the element on the host3.instance1 data instance handles all transactions for the replica set. Once the element on the host4.instance1 data instance recovers, both elements in the replica set can handle transactions.
Figure 11-1 K-safety reacts to one data instance failure

Description of ''Figure 11-1 K-safety reacts to one data instance failure''
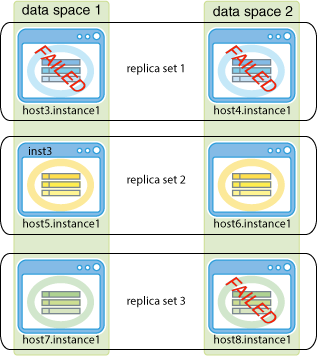
Multiple failures in different replica sets do not result in loss of functionality, as long as there is one element up in each replica set. You may lose data if an entire replica set fails.
The following example shows a grid where k = 2 with three replica sets. In this example, the elements in the host4.instance1, host5.instance1, and host8.instance1 data instances fail. However, your transactions continue to execute since there is at least one element available in each replica set.
Figure 11-2 K-safety reacts to multiple data instance failures
Description of ''Figure 11-2 K-safety reacts to multiple data instance failures''
Recovering when a single element fails in a replica set
See the following sections on how to respond when a single element fails within a replica set when k=2:
Troubleshooting based on element status
For some of the element states, you may be required to intervene. When you display the element status, you can respond to each of these element states. Table 11-2 shows details on each element status and a recommendation of how to respond to changes in the element status.
| Status | Meaning | Notes and recommendations |
|---|---|---|
|
|
The attempt to close the element failed. |
Refer to the You can try |
|
|
The element is in the process of closing. |
Wait, and run the |
|
|
The attempt to create the element failed. |
Refer to the You can use the |
|
|
The element is being created. |
Wait, and run the |
|
|
The attempt to destroy the element failed. |
Refer to the If the element status is |
|
|
The element has been destroyed. |
Element no longer exists. Note: When the last element of a database is destroyed, no record of the database, including element status, will exist. |
|
|
The element is being destroyed. |
Wait, and run the |
|
|
The data instance where this element is located is not running. |
If the data instance is down, the status of an element is down. Try to restart the data instance by using the See Example 11-3, "Restart a data instance that is down" and "Recovering when a data instance is down" for more details on how to manually restart a data instance. |
|
|
The element was evicted or removed through |
When the element status is |
|
|
The element was evicted or removed through |
Wait, and run When the element status is |
|
|
The element was evicted or removed through |
Wait, and run When the element status is |
|
|
The attempt to load the element failed. |
Refer to the You can try again to load the element with the |
|
|
The element is loaded. |
Element is loaded and can now be opened. You can confirm if the element is in the distribution map with the |
|
|
The element is being loaded. |
Wait, and run the |
|
|
The element is open. |
Normal status for a functioning element. Database connections are possible through the element. |
|
|
The attempt to open the element failed. |
Refer to the You can try |
|
|
The element is in the process of opening. |
Wait, and run |
|
|
The element should be created, but creation has not yet started. |
Wait, and run the |
|
|
The element has been unloaded. |
Database is ready to be loaded again ( You can run the |
|
|
The element is being unloaded. |
Wait, and run the |
|
|
The element will be loaded, but not until after the other element in its replica set is loaded. |
Note the status of the other element in the replica set.
|
Note:
The notes and recommendations column often refers tottGridAdmin commands. For more information on these commands within the Oracle TimesTen In-Memory Database Reference, see "Monitor the status of a database (dbStatus)" for ttGridAdmin dbStatus, "Create a database (dbCreate)" for ttGridAdmin dbCreate, "Open a database (dbOpen)" for ttGridAdmin dbOpen, "Load a database into memory (dbLoad)" for ttGridAdmin dbLoad, "Unload a database (dbUnload)" for ttGridAdmin dbUnload, "Close a database (dbClose)" for ttGridAdmin dbClose, "Destroy a database (dbDestroy)" for ttGridAdmin dbDestroy, and "Execute a command or script on grid instances (instanceExec)" for ttGridAdmin instanceExec.The following sections demonstrate how to respond with different scenarios where a single element in the replica set has failed:
Example 11-2 Retrying element creation
If the creation of the element failed, then retry the creation of the element with the ttGridAdmin dbCreate -instance command on the same data instance where the element should exist.
% ttGridAdmin dbCreate database1 -instance host3 Database database1 creation started
Example 11-3 Restart a data instance that is down
When a data instance is down, the element within the data instance is down. You restart the daemon of the data instance by using the ttGridAdmin instanceExec -only command to execute the ttDaemonAdmin -start command. See "Recovering when a data instance is down" for more details.
% ttGridAdmin instanceExec -only host4.instance1 ttDaemonAdmin -start Overall return code: 0 Commands executed on: host4.instance1 rc 0 Return code from host4.instance1: 0 Output from host4.instance1: TimesTen Daemon (PID: 15491, port: 14000) startup OK.
Example 11-4 Destroying an evicted element or an element where a destroy failed
If you evict an element, you still need to destroy the element to free up the file system space used by the element. After which, you may decide to create a new element. See "Unavailability of data when a full replica set is down or fails" for more details on eviction.
When the element status is destroy failed or evicted, destroy the element of the data instance with the ttGridAdmin dbDestroy -instance command.
% ttGridAdmin dbDestroy database1 -instance host3 Database database1 destroy started
Recovering a replica set after an element goes down
When k = 2, all active elements in the same replica set are transactionally synchronized. Any DML or DDL statements applied to one element in a replica set are also applied to all other elements in the replica set. When one element in the replica set is not up, the other element can continue to execute DML or DDL statements.
-
If the failed element recovers, it was unavailable for a time and fell behind transactionally. Before this element can resume its part in the replica set in the grid, it must synchronize its data with the active element of its replica set.
-
If the element permanently fails, such as a file system failure, you need to remove that element from the replica set and replace it with another element with the
ttGridAdmin dbDistribute -remove -replaceWithcommand. See "Replace an element with another element" for details.
TimesTen Scaleout automatically re-synchronizes and restores the data on the restored or new element in the replica set with the following methods:
-
Log-based catch up: This process transfers the transaction logs from the active element in the replica set and applies transaction records that are missing on the recovering element. This operation applies the DML or DDL statements that occurred while the element was not participating in the replica set.
Transactions that are started while one of the elements of the replica set is down must be replayed when recovering the down element. The log-based catch up process waits for any open transactions to commit or roll back before replaying them from the transaction log. If the down element is in the recovery process for an extended period of time, then there may be an open transaction (on the active element) preventing the completion of the log-based catch up process for the recovering element. Use the
ttXactAdminutility to check for open transactions. Resolve any open transactions by either committing or rolling them back. -
Duplicate: TimesTen Scaleout duplicates the active element either to a recovering element or to a new element that replaces a failed element. The duplication operation copies all checkpoint and log files of the active element to the recovering element.
However, since the active element continues to accept transactions during the duplicate operation, there may be additional transaction log records that are not a part of the copied transaction log files. After completing the duplicate operation, TimesTen Scaleout contacts the active element and performs a log-based catch up operation to bring the new element completely up to date.
Remove and replace a failed element in a replica set
When k = 2, if an element cannot be recovered automatically, then you have to investigate what caused the failure. You may discover a problem that can be fixed, such as a drive that needs to be remounted. However, you may discover a problem that cannot be fixed, such as a drive that is completely destroyed. Most permanent, unrecoverable failures are normally related to hardware failures.
-
If you can, fix the problem with the host or the data instance and then perform one of the following:
-
Restart the data instance. See "Recovering when a data instance is down" for directions on how to restart the data instance.
-
Reload the TimesTen database with the
ttGridAdmin dbloadcommand, which attempts to reload the element.
-
-
If you cannot fix the problem with the host or data instance, then the data on the element may be in a state where it cannot be retrieved. In this case, you must remove the element and replace it with another element. Once replaced, the active element updates the new element with the data for this replica set.
If one of your hosts is encountering multiple errors (even though it has been able to automatically recover), you may decide to replace it with another host that is more reliable.
To replace an element without data loss, execute the ttGridAdmin dbDistribute -remove -replaceWith command, which takes the data that exists on the element you want to replace and redistributes to a new element. See "Replace an element with another element" for more details.
Unavailability of data when a full replica set is down or fails
If all elements in a single replica set are down or failed, the data stored in the down replica set is unavailable. In order to guard against full replica set failure, distribute your elements in a way that reduces the chances of full replica set failure. See "Assigning hosts to data space groups" for details on installing data instances on hosts that are physically separated from each other.
The following sections describe the transaction behavior when a replica set is down, how TimesTen Scaleout may recover the replica set, and what you can do if the replica set needs intervention to fully recover.
Recovering from a down replica set
As described in Table 11-3, if you have a down or failed replica set, the outcome of preserving your data successfully may depend on how you set the Durability connection attribute. See "Durability settings" for more details on Durability connection attribute settings.
Table 11-3 Potential for transaction recovery based on Durability value
| Durability value | Affect on transactions when a replica set fails |
|---|---|
|
1 |
Participants synchronously write a prepare-to-commit or commit log record to the transaction log for distributed transactions. This ensures that committed transactions have the best possible chance of being preserved. If a replica set goes down, all transaction log records have been durably committed to the file system and can be recovered by TimesTen Scaleout. |
|
0 |
Participants asynchronously write prepare-to-commit and commit log records for distributed transactions. If an entire replica set goes down, transaction log records are not guaranteed to be durably committed to the file system. There is a chance for data loss, depending on how the elements within the replica set fail or go down. |
The following sections describe what happens with new transactions after a replica set goes down or how the replica set recovers depends on the Durability connection attribute value.
Transaction behavior with a down replica set
The following list describes what occurs for your transaction when there is a down replica set.
-
Transactions with queries that access rows only within active replica sets (and no rows within a down replica set) succeed. Queries that try to access data within a down replica set fail. Your application should retry the transaction when the replica set has recovered.
A global read with a partial results hint that does not require data from the down replica set succeeds.
For example, if both elements in replica set 1 failed and the queries within the transaction require data from replica set 1, then the transaction fails. Your application should perform the transaction again.
-
Transactions with any DDL statement fail when there is a down replica set as DDL statements require all replica sets to be available. Your application should roll back the transaction.
-
Transactions with any DML statements fail if the transaction tries to update at least one row on elements in a down replica set. Your application should roll back the transaction. When
Durability=0, this scenario may encounter data loss. See "Recovering a failed replica set when Durability=0" for full details. -
When
Durability=1, transactions with DML that do not require data from the down replica set succeeds. For example, if both elements in replica set 1 failed, then the transaction succeeds only if anySELECT,INSERT,INSERT...SELECT,UPDATEorDELETEstatements do not depend on data that was stored in replica set 1.
Durably recovering a failed replica set when Durability=1
The following sections describe the process for recovery of a failed replica set when Durability=1.
If all elements in the replica set go down, even temporarily, TimesTen Scaleout might be able to automatically recover the full replica set (if the initial issue is resolved) by:
-
Determining and recovering the seed element. The element that failed with the latest changes, known as the seed element, is recovered first. The seed element is recovered to the latest transaction in the checkpoint and transaction log files.
-
After recovery of the element is complete, TimesTen Scaleout checks for in-doubt transactions.
When an element is loaded from the file system (from checkpoint and transaction log files) to recover after a transient failure or unexpected termination, any two-phase commit transactions that were prepared, but not committed, are left pending. This is referred to as an in-doubt transaction. When a transaction has been interrupted, there may be a doubt of whether the entire transaction was committed with the two-phase commit protocol.
-
If there are no in-doubt transactions, operation proceeds as normal.
-
If there are in-doubt transactions, normal processing that includes this replica set does not continue until all in-doubt transactions are resolved. If there are any in-doubt transactions, TimesTen Scaleout checks the transaction log to determine whether the transaction committed or was prepared to commit on any of the participants. The transaction log records contain information about other participants in the transaction. See Table 11-4 for how TimesTen Scaleout resolves in-doubt transactions.
If an element fails during this process and then comes back up after the transaction commits or rolls back, the element recovers itself by requesting the result of the other participating elements.
-
-
After the seed element is recovered, the other element in the replica set is recovered from the seed element using the duplicate and log-based catch up methods. See "Recovering a replica set after an element goes down" for details on the duplicate and log-based catch up methods.
Table 11-4 How TimesTen Scaleout resolves an in-doubt transaction
| Failure | Action |
|---|---|
|
At least one participant received the commit log record; all other participants at least receive the prepare-to-commit log record. |
The transaction commits on all participants |
|
All participants in the transaction received the prepare-to-commit log record. |
The transaction commits on all participants. |
|
At least one participant did not receive the prepare-to-commit log record. |
The transaction manager notifies all participants to undo the prepare-to-commit, which is a prelude to a roll back of the transaction.
|
However, if you cannot recover the elements in a down replica set, then you may need to either remove and replace one of the elements or evict the entire replica set. See "Recovering when the replica set has a permanently failed element" for details.
Recovering a failed replica set when Durability=0
The following describes the process for recovery of a failed replica set when Durability=0.
If you set Durability=0, you are acknowledging that there is a chance of data loss when a replica set fails. However, TimesTen Scaleout attempts to avoid data loss if the elements fail at separate times.
-
If only a single element of the replica set fails, then TimesTen Scaleout attempts to switch the remaining element in the replica set (when k = 2) into durable mode. That is, in order to limit data loss (which would occur if the remaining element fails when
Durability=0), TimesTen Scaleout changes the durability behavior of the element as if it was configured withDurability=1.If TimesTen Scaleout can switch the remaining element in the replica set into durable mode, then the participating element synchronously writes prepare-to-commit log records to the file system for distributed transactions. Then, if this element also fails so that the entire replica set is down, TimesTen Scaleout recovers the replica set from the transaction log records. Thus, no transaction is lost in this scenario and TimesTen Scaleout automatically recovers the replica set as when you have set
Durability=1. See "Durably recovering a failed replica set when Durability=1" for details on recovering after the single element is recovered. -
If TimesTen Scaleout cannot switch the replica set into durable mode before the final surviving element fails, then you may encounter data loss depending on whether the replica set encounters a temporary or permanent failure.
-
Temporary replica set failure when elements are non-durable: Since neither element in the replica set synchronously wrote prepare-to-commit log records for distributed transactions that the replica set was involved in before going down, then any transactions that committed after the last successful epoch transaction are lost.
If both elements show the
waiting for seedstatus, then there was no switch into durable mode before the replica set went down. If this is the case, epoch recovery is necessary and any transactions committed after latest successful epoch transaction are lost. When the elements in this replica set recover, they may remain in thewaiting for seedstatus, since neither element is able to recover with the transaction logs. Instead, you must perform epoch recovery by either recovering or evicting the replica set, followed by unloading and reloading the database. See "Process when replica set fails when in a non-durable state" for details. -
Permanent replica set failure: If you cannot recover either element in the replica set, you may have to evict these elements. This results in a loss of the data on that replica set. See "Recovering when the replica set has a permanently failed element" for details.
-
Process when replica set fails when in a non-durable state
When a replica set goes down and the state is non-durable, transactions may continue to commit into the database until TimesTen Scaleout realizes that the replica set is down. Once TimesTen Scaleout realizes that a replica set is down (after a failed epoch transaction execution), then the database is switched to read-only to minimize the number of lost transactions. During epoch recovery, the database is reloaded to the last successful epoch transaction, effectively losing any transactions that committed after that last successful epoch transaction. In this scenario, the value of the EpochInterval connection attribute not only determines the amount of time between the epoch transactions, but also determines the approximate amount of time during which you can lose committed transactions.
Note:
The database is set to read-only when the epoch transaction fails due to a down replica set; TimesTen Scaleout does not set the database to read-only if the epoch transaction fails for other reasons.Figure 11-3 shows the actions across a time span of eight intervals.
Figure 11-3 Durability=0 and a replica set fails
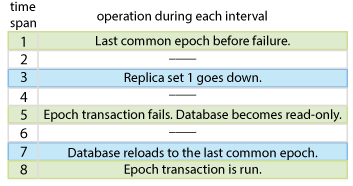
Description of ''Figure 11-3 Durability=0 and a replica set fails''
-
An epoch transaction commits successfully.
-
Transactions may continue after the successful epoch transaction. Any committed transactions after the last successful epoch transaction are lost after epoch recovery as neither element in the down replica set was able to durably flush the transaction logs.
-
Replica set 1 goes down without either element switching to durable mode.
Note:
Sequences may be incremented while the replica set is down. -
Transactions may continue after the replica set goes down if the database has not yet been set to read-only. Any transactions that commit after the last successful epoch transaction are lost after epoch recovery as neither element in the down replica set was able to durably flush the transaction logs.
Note:
The behavior of transactions after a replica set goes down depends on the type of statements within the transactions, as described in "Transaction behavior with a down replica set". -
The next epoch transaction fails since not all replica sets are up. TimesTen Scaleout informs all data instances that the database is now read-only. All applications will fail when executing a DML, DDL, or commit statements within open transactions. You must roll back each transaction.
Note:
ThettGridAdmin dbStatuscommand shows the state of the database, including if it is in read-only or read-write mode. -
The replica set must be recovered or evicted.
-
Recover the down replica set. If multiple replica sets are down, the database cannot enter read-write mode until all replica sets are recovered or replaced.
-
If you cannot recover either element in the replica set, you may have to evict the replica set, which results in a loss of the data on that replica set. See "Recovering when the replica set has a permanently failed element" for details.
-
-
You perform an epoch recovery by unloading and reloading the database to the last successful epoch transaction to recover the database consistently with only a partial data loss. Any transactions that commit after the last successful epoch are lost when the database is unloaded and reloaded to the last successful epoch transaction. See "Load a database into memory (dbLoad)" for information on the
ttGridAdmin dbLoadcommand and "Unload a database (dbUnload)" for information on thettGridAdmin dbUnloadcommand. -
A new epoch transaction is successful. Database is set to read-write. Normal transaction behavior resumes.
Note:
If you want to ensure that the data for a transaction is always recovered, you can promote a transaction to be an epoch transaction. See "Epoch transactions" for more details.Recovering when the replica set has a permanently failed element
If an element in the replica set or a full replica set is unrecoverable because there has been a permanent failure, then you need to remove the failed element or evict the failed replica set. Permanent failure can occur when a host permanently fails or if all elements in the replica set fail.
-
If all elements within a replica set permanently fail, you must evict the entire replica set, which results in the permanent loss of the data on the elements within that replica set.
When k = 1, then the permanent failure of one element is a replica set failure. When k = 2, both elements in a replica set must fail in order for the replica set to be considered failed. If k = 2 and the replica set permanently fails, you need to evict both elements of the replica set simultaneously.
Evicting the replica set removes it from the distribution for the grid. However, you cannot evict the replica set if the failed replica set is the only replica set in the database. In this case, save any checkpoint files, transaction log files or daemon log files (if possible) and then destroy and recreate the database.
When a replica set goes down:
-
If
Durability=0, the database goes into read-only mode. -
If
Durability=1, then all transactions that include the failed replica set are blocked until you evict the failed replica set. However, all transactions that do not involve the failed replica set continue to work as if nothing was wrong.
-
-
If k = 2 and only one element of a replica set fails, the active element takes over all of the requests for data until the failed element can be replaced with a new element. Thus, no data is lost with the failure. The active element in the replica set processes the incoming transactions. You can simply remove and replace the failed element with a new element that is duplicated from the active element in the replica set. The active element provides the base for a duplicate for the new element. See "Replace an element with another element" for details on how to remove and replace a failed element.
Note:
If you know about problems that TimesTen Scaleout is not aware of and that a replica set needs to be evicted, you can evict and replace a replica set as needed.You can evict the replica set from the distribution map for your grid with the ttGridAdmin dbDistribute -evict command. Make sure that all pending requests for adding or removing elements are applied before requesting the eviction of a replica set.
You have the following options when you evict a replica set:
-
Evict the replica set without replacing it immediately.
If the data instances and hosts for this replica set have not failed, then you can recreate the replica set using the same data instances. This is a preferred option if there are other databases on the grid and the hosts are fine.
In this case, you must:
-
Evict the elements of the failed replica set, while the data instances and hosts are still up.
When you evict the replica set, the data is lost within this replica set, but the other replica sets in the database continue to function. There is now one fewer replica set in your grid.
-
Eliminate all checkpoint and transaction logs for the elements within the evicted replica set if you want to add new elements to the distribution map on the same data instances which previously held the evicted elements.
-
Destroy the elements of the evicted replica set, while the data instances and hosts are still up.
-
Optionally, you can replace the evicted replica set with a new replica set either on the same data instances and hosts if they are still viable or on new data instances and hosts. Add the new elements to the distribution map. This restores the grid to its expected configuration.
-
-
Evict the replica set and immediately replace it with a new replica set to restore the grid to its expected configuration.
-
Create new data instances and hosts to replace the data instances and hosts of the failed replica set.
-
Evict the elements of the failed replica set, while replacing it with a new replica set. When you evict the replica set, the data is lost within this replica set, but the other replica sets in the database continue to function.
Use the
ttGridAdmin dbDistribute -evict -replaceWithcommand to evict and replace the replica set with a new replica set, where each new element is created on a new data instance and host. The elements of the new replica set are added to the distribution map. However, the remaining data from the other replica sets are not redistributed to include the new replica. Thus, the new replica set remains empty until you insert data. -
Destroy the elements of the evicted replica set.
-
The following sections demonstrate how to evict a failed replica set when you have one or two elements in the replica set:
-
Evicting the element in the permanently failed replica set when k = 1
-
Evicting all elements in a permanently failed replica set when k = 2
Evicting the element in the permanently failed replica set when k = 1
The example shown in Figure 11-4 shows a TimesTen database that has been configured with k set to 1 with three data instances: host1.instance1, host2.instance1 and host3.instance1. The element on the host2.instance1 data instance fails because of a permanent hardware failure.
The following examples demonstrate the eviction options:
-
Example 11-5, "Evict the element to potentially replace at another time"
-
Example 11-6, "Evict and replace the data instance without re-distribution"
Example 11-5 Evict the element to potentially replace at another time
If you cannot recover a failed element, you evict the replica set.
The following example:
-
Evicts the replica set for the element on the
host2.instance1data instance with thettGridAdmin dbDistribute -evictcommand. -
Destroys the checkpoint and transaction logs for only this element within the evicted replica set with the
ttGridAdmin dbDestroy -instancecommand.Note:
Alternatively, see the instructions in "Remove and replace a failed element in a replica set" if the data instance or host on which the element exists is not reliable.
% ttGridAdmin dbDistribute database1 -evict host2.instance1 -apply
Element host2.instance1 evicted
Distribution map updated
% ttGridAdmin dbDestroy database1 -instance host2.instance1
Database database1 instance host2 destroy started
% ttGridAdmin dbStatus database1 -all
Database database1 summary status as of Thu Feb 22 16:44:15 PST 2018
created,loaded-complete,open
Completely created elements: 2 (of 3)
Completely loaded elements: 2 (of 3)
Open elements: 2 (of 3)
Database database1 element level status as of Thu Feb 22 16:44:15 PST 2018
Host Instance Elem Status Date/Time of Event Message
----- --------- ---- --------- ------------------- -------
host1 instance1 1 opened 2018-02-22 16:42:14
host2 instance1 2 destroyed 2018-02-22 16:44:01
host3 instance1 3 opened 2018-02-22 16:42:14
Database database1 Replica Set status as of Thu Feb 22 16:44:15 PST 2018
RS DS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host1 instance1 opened 2018-02-22 16:42:14
2 1 3 host3 instance1 opened 2018-02-22 16:42:14
Database database1 Data Space Group status as of Thu Feb 22 16:44:15 PST 2018
DS RS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host1 instance1 opened 2018-02-22 16:42:14
2 3 host3 instance1 opened 2018-02-22 16:42:14
This example creates a new element for the replica set as the data instance and host are still viable. Then, adds the new elements to the distribution map.
-
Creates a new element with the
ttGridAdmin dbCreate -instancecommand on the same data instance where the previous element existed before its replica set was evicted. -
Adds the new element into the distribution map with the
ttGridAdmin dbDistribute -addcommand.
% ttGridAdmin dbCreate database1 -instance host2
Database database1 creation started
% ttGridAdmin dbDistribute database1 -add host2 -apply
Element host2 is added
Distribution map updated
% ttGridAdmin dbStatus database1 -all
Database database1 summary status as of Thu Feb 22 16:53:17 PST 2018
created,loaded-complete,open
Completely created elements: 3 (of 3)
Completely loaded elements: 3 (of 3)
Open elements: 3 (of 3)
Database database1 element level status as of Thu Feb 22 16:53:17 PST 2018
Host Instance Elem Status Date/Time of Event Message
----- --------- ---- ------ ------------------- -------
host1 instance1 1 opened 2018-02-22 16:42:14
host3 instance1 3 opened 2018-02-22 16:42:14
host2 instance1 4 opened 2018-02-22 16:53:14
Database database1 Replica Set status as of Thu Feb 22 16:53:17 PST 2018
RS DS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host1 instance1 opened 2018-02-22 16:42:14
2 1 3 host3 instance1 opened 2018-02-22 16:42:14
3 1 4 host2 instance1 opened 2018-02-22 16:53:14
Database database1 Data Space Group status as of Thu Feb 22 16:53:17 PST 2018
DS RS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host1 instance1 opened 2018-02-22 16:42:14
2 3 host3 instance1 opened 2018-02-22 16:42:14
3 4 host2 instance1 opened 2018-02-22 16:53:14
Example 11-6 Evict and replace the data instance without re-distribution
To recover the initial capacity with the same number of replica sets as you started with for the database, evict and replace the evicted element using the ttGridAdmin dbDistribute -evict -replaceWith command.
The following example:
-
Creates a new host (identified as
host4), installation, data instance and element. -
Evicts the replica set that contains the failed element on the
host2.instance1data instance and replaces the evicted element with the element on thehost4.instance1data instance using thettGridAdmin dbDistribute-evict-replaceWithcommand.The data that exists on the elements on the
host1.instance1andhost3.instance1data instances is not redistributed to the new element on thehost4.instance1data instance. The element on thehost4.instance1data instance is empty. -
Destroys the element on the
host2.instance1data instance with thettGridAdmin dbDestroy -instancecommand.
% ttGridAdmin hostCreate host4 -address myhost.example.com -dataspacegroup 1
Host host4 created in Model
% ttGridAdmin installationCreate -host host4 -location /timesten/host4/installation1
Installation installation1 on Host host4 created in Model
% ttGridAdmin instanceCreate -host host4 -location /timesten/host4
Instance instance1 on Host host4 created in Model
% ttGridAdmin modelApply
Copying Model.........................................................OK
Exporting Model Version 2.............................................OK
Marking objects 'Pending Deletion'....................................OK
Deleting any Hosts that are no longer in use..........................OK
Verifying Installations...............................................OK
Creating any missing Installations....................................OK
Creating any missing Instances........................................OK
Adding new Objects to Grid State......................................OK
Configuring grid authentication.......................................OK
Pushing new configuration files to each Instance......................OK
Making Model Version 2 current........................................OK
Making Model Version 3 writable.......................................OK
Checking ssh connectivity of new Instances............................OK
Starting new data instances...........................................OK
ttGridAdmin modelApply complete
% ttGridAdmin dbDistribute database1 -evict host2.instance1
-replaceWith host4.instance1 -apply
Element host2.instance1 evicted
Distribution map updated
% ttGridAdmin dbDestroy database1 -instance host2
Database database1 instance host2 destroy started
% ttGridAdmin dbStatus database1 -all
Database database1 summary status as of Thu Feb 22 17:04:21 PST 2018
created,loaded-complete,open
Completely created elements: 3 (of 4)
Completely loaded elements: 3 (of 4)
Open elements: 3 (of 4)
Database database1 element level status as of Thu Feb 22 17:04:21 PST 2018
Host Instance Elem Status Date/Time of Event Message
----- --------- ---- --------- ------------------- -------
host1 instance1 1 opened 2018-02-22 16:42:14
host3 instance1 3 opened 2018-02-22 16:42:14
host2 instance1 4 destroyed 2018-02-22 17:04:11
host4 instance1 5 opened 2018-02-22 17:03:18
Database database1 Replica Set status as of Thu Feb 22 17:04:21 PST 2018
RS DS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host1 instance1 opened 2018-02-22 16:42:14
2 1 3 host3 instance1 opened 2018-02-22 16:42:14
3 1 5 host4 instance1 opened 2018-02-22 17:03:18
Database database1 Data Space Group status as of Thu Feb 22 17:04:21 PST 2018
DS RS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ----- --------- ------ ------------------- -------
1 1 1 host1 instance1 opened 2018-02-22 16:42:14
2 3 host3 instance1 opened 2018-02-22 16:42:14
3 5 host4 instance1 opened 2018-02-22 17:03:18
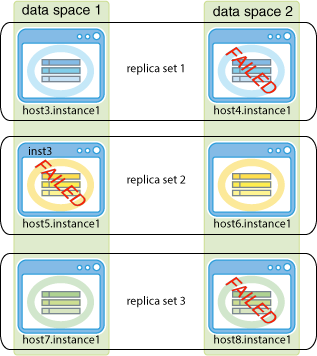
Evicting all elements in a permanently failed replica set when k = 2
If k = 2 and the replica set permanently fails, then you need to evict both elements of the replica set simultaneously.
Figure 11-5 shows where replica set 1 fails.
For the example shown in Figure 11-5, replica set 1 contains elements that exist on both the host3.instance1 and host4.instance1 data instances. The replica set fails in an unrepairable way. When you execute the ttGridAdmin dbDistribute command to evict the replica set, specify the data instances of both elements in the replica set that are being evicted.
% ttGridAdmin dbDistribute database1 -evict host3.instance1 -evict host4.instance1 -apply Element host3.instance1 evicted Element host4.instance1 evicted Distribution map updated
Replacing the replica set with new elements with no data redistribution
If you cannot recover either element in the replica set, you evict both elements in the replica set simultaneously. To recover the initial capacity with the same number of replica sets as you started with for the database, evict and replace the evicted elements in the failed replica set using the ttGridAdmin dbDistribute -evict -replaceWith command.
The following example:
-
Creates new elements in the
host9.instance1andhost10.instance1data instances. -
Evicts the replica set with the failed elements on the
host3.instance1andhost4.instance1data instances, replacing them with new elements in thehost9.instance1andhost10.instance1data instances.The data that exists on the elements in the active replica sets is not redistributed to include the new elements on the
host9.instance1andhost10.instance1data instances. The elements on thehost9.instance1andhost10.instance1data instances are empty. -
Destroys the elements on the
host3.instance1andhost4.instance1data instances with thettGridAdmin dbDestroy -instancecommand.The new replica set is now listed as replica set 1 with the elements from the replaced elements located in the
host9.instance1andhost10.instance1data instances.
% ttGridAdmin hostCreate host9 -internalAddress int-host9 -externalAddress
ext-host9.example.com -like host3 -cascade
Host host9 created in Model
Installation installation1 created in Model
Instance instance1 created in Model
% ttGridAdmin hostCreate host10 -internalAddress int-host10 -externalAddress
ext-host10.example.com -like host4 -cascade
Host host10 created in Model
Installation installation1 created in Model
Instance instance1 created in Model
% ttGridAdmin dbDistribute database1 -evict host3.instance1
-replaceWith host9.instance1 -evict host4.instance1
-replaceWith host10.instance1 -apply
Element host3.instance1 evicted
Element host4.instance1 evicted
Distribution map updated
% ttGridAdmin dbStatus database1 -all
Database database1 summary status as of Fri Feb 23 10:22:57 PST 2018
created,loaded-complete,open
Completely created elements: 8 (of 8)
Completely loaded elements: 6 (of 8)
Completely created replica sets: 3 (of 3)
Completely loaded replica sets: 3 (of 3)
Open elements: 6 (of 8)
Database database1 element level status as of Fri Feb 23 10:22:57 PST 2018
Host Instance Elem Status Date/Time of Event Message
------ --------- ---- ------- ------------------- -------
host3 instance1 1 evicted 2018-02-23 10:22:28
host4 instance1 2 evicted 2018-02-23 10:22:28
host5 instance1 3 opened 2018-02-23 07:28:23
host6 instance1 4 opened 2018-02-23 07:28:23
host7 instance1 5 opened 2018-02-23 07:28:23
host8 instance1 6 opened 2018-02-23 07:28:23
host10 instance1 7 opened 2018-02-23 10:22:27
host9 instance1 8 opened 2018-02-23 10:22:27
Database database1 Replica Set status as of Fri Feb 23 10:22:57 PST 2018
RS DS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ------ --------- ------ ------------------- -------
1 1 8 host9 instance1 opened 2018-02-23 10:22:27
2 7 host10 instance1 opened 2018-02-23 10:22:27
2 1 3 host5 instance1 opened 2018-02-23 07:28:23
2 4 host6 instance1 opened 2018-02-23 07:28:23
3 1 5 host7 instance1 opened 2018-02-23 07:28:23
2 6 host8 instance1 opened 2018-02-23 07:28:23
Database database1 Data Space Group status as of Fri Feb 23 10:22:57 PST 2018
DS RS Elem Host Instance Status Date/Time of Event Message
-- -- ---- ------ --------- ------ ------------------- -------
1 1 8 host9 instance1 opened 2018-02-23 10:22:27
2 3 host5 instance1 opened 2018-02-23 07:28:23
3 5 host7 instance1 opened 2018-02-23 07:28:23
2 1 7 host10 instance1 opened 2018-02-23 10:22:27
2 4 host6 instance1 opened 2018-02-23 07:28:23
3 6 host8 instance1 opened 2018-02-23 07:28:23
% ttGridAdmin dbDestroy database1 -instance host3
Database database1 instance host3 destroy started
% ttGridAdmin dbDestroy database1 -instance host4
Database database1 instance host4 destroy started
Maintaining database consistency after an eviction
Eviction of an entire replica set results in data loss, which can leave the database in an inconsistent state. For example, if the parent records were stored in an evicted replica set, then any child rows on other elements in a different replica set are in a table without a corresponding foreign key parent.
To ensure that you maintain database consistency after an eviction, fix all foreign key references by performing one of the following steps:
-
Delete any child row that does not have a corresponding parent.
-
Drop the foreign key constraint for any child row that does not have a corresponding parent.
Recovering when a data instance is down
If the error is a hardware error involving the host, then fix the problem with the host and reload the data instance with the ttGridAdmin dbLoad command. During reload, TimesTen Scaleout attempts to recover the element within that data instance.
If a data instance is down, you should restart it. If a data instance is not running, then all of the elements that the data instance manages are down.
The ttGridAdmin dbStatus -element command shows if a data instance (and thus its element) is considered down.
% ttGridAdmin dbStatus database1 -element Database database1 element level status as of Wed Mar 8 14:07:11 PST 2017 Host Instance Elem Status Date/Time of Event Message ----- --------- ---- ------ ------------------- ------- host3 instance1 1 opened 2017-03-08 13:58:06 host4 instance1 2 down host5 instance1 3 opened 2017-03-08 13:58:06 host6 instance1 4 opened 2017-03-08 13:58:09 host7 instance1 5 opened 2017-03-08 13:58:09 host8 instance1 6 opened 2017-03-08 13:58:09
When a data instance is down (due to a hardware or software failure), all communication channels to its managed elements are shut down and no new connections are allowed to access these elements until all the data instance is restored and the element that it manages is recovered.
If the data instance is down, you restart it by restarting its TimesTen daemon. Once restarted, the data instance connects to a ZooKeeper server. If it does not immediately connect, it continues to try to connect to a ZooKeeper server. After connection, the data instance loads its element.
Note:
If the data instance fails to connect to any ZooKeeper server, it may be in an unending loop as it continues to try to connect.You can manually restart the daemon for that data instance by using the instanceExec command to execute the TimesTen ttDaemonAdmin -start command, using the instanceExec command options of -only hostname[.instancename].
% ttGridAdmin instanceExec -only host4.instance1 ttDaemonAdmin -start Overall return code: 0 Commands executed on: host4.instance1 rc 0 Return code from host4.instance1: 0 Output from host4.instance1: TimesTen Daemon (PID: 15491, port: 14000) startup OK.
For more information, see "Execute a command or script on grid instances (instanceExec)" in the Oracle TimesTen In-Memory Database Reference or "ttDaemonAdmin" in the Oracle TimesTen In-Memory Database Reference.
If you know what caused the error that caused the data instance to fail, then reload the database with the ttGridAdmin dbLoad command after you fix the problem.
% ttGridAdmin dbLoad database1
You can verify the results with the ttGridAdmin dbStatus command.
Database recovery
You reload the database to initiate database recovery when either all of the data instances are down or both elements in a replica set show the waiting for seed state.
To reload the database:
-
Run the
ttGridAdmin dbStatuscommand to see the status of all elements within their respective replica sets. -
Resolve any issues with the elements of the database, as denoted by each element status, as described in Table 11-2, "Element status".
-
Execute the
ttGridAdmin dbloadcommand to reload your database, as described in "Reloading a database into memory".
Note:
If an element of a replica set shows thewaiting for seed status, but the seed element does not recover, then evaluate the host and data instance for that element to see if you need to intervene on either a hardware or software error.
If the seed element still does not recover after reloading the database, then evict the down replica set. See "Recovering when the replica set has a permanently failed element" for details. If Durability=0, then evict the replica set and then unload and reload the database to perform epoch recovery. See "Recovering a failed replica set when Durability=0" for details.
Client connection failover
When constructing a highly available system, you want to ensure that:
-
Client application connections are automatically routed to an active data instance for that database.
-
If an existing client connection to a data instance fails, the client is automatically reconnected to another active data instance in the database.
-
If the data instance to which a client is connected fails, then that client is automatically reconnected to another active data instance in the database.
Note:
See "Connecting to a database" for details on how a client connects to a data instance in a grid.By default, if a connection fails, then the client automatically attempts to reconnect to another data instance (if possible). Consider the following details on how to prepare for and respond to a connection failure:
-
The
TTC_REDIRECTclient connection attribute defines how a client is redirected. By default,TTC_REDIRECTis set to 1 for automatic redirection. If set to 0 and the initial connection attempt to the desired data instance fails, then an error is returned and there are no further connection attempts. See "TTC_REDIRECT" in the Oracle TimesTen In-Memory Database Reference for more details. -
The
TTC_NoReconnectOnFailoverclient connection attribute defines whether TimesTen should reconnect after a failover. The default is 0, which indicates that TimesTen should attempt to reconnect. Setting this to 1 specifies that TimesTen performs typical client failover, but without reconnecting. This is useful where an application does its own connection pooling or attempts to reconnect to the database on its own after failover. See "TTC_NoReconnectOnFailover" in the Oracle TimesTen In-Memory Database Reference for more details. -
Most connection failures tend to be software failures. Reconnecting to another data instance takes some time during which the connection is not available until the client failover process is completed. Any attempt to use the connection during the client failover processing time generates a native error. See "JDBC support for automatic client failover" in the Oracle TimesTen In-Memory Database Java Developer's Guide or "Using automatic client failover in your application" in the Oracle TimesTen In-Memory Database C Developer's Guide for the native errors that can be received.
-
If you receive a native error in response to an operation within your application, your application should place all recovery actions within a loop with a short delay before each subsequent attempt, where the total number of attempts is limited. If you do not limit the number of attempts, then the application may appear to hang if the client failover process does not complete successfully. See "Application action in the event of failover" in the Oracle TimesTen In-Memory Database Java Developer's Guide or "Application action in the event of failover" in the Oracle TimesTen In-Memory Database C Developer's Guide for an example on how to write a retry block within your application for automatic client failover.
Configuring TCP keep-alive parameters
One of the ways that a client connection can fail is with a network failure, such as disconnecting a cable or a host that is hanging or crashing. When the client connection is lost, then client connection failover is initiated. However, when a TCP connection is started, you can configure the TCP keep-alive parameters for the connection to ensure reliable and rapid detection of connection failures.
Note:
You can also detect that there is a problem with the connection by setting theTTC_Timeout attribute, which sets a maximum time limit for a network operation that is completed by using the TimesTen client and server. The TTC_Timeout attribute also determines the maximum number of seconds a TimesTen client application waits for the result from the corresponding TimesTen Server process before timing out.
TimesTen Scaleout recommends configuring the TCP keep-alive parameters for determining a failed TCP connection in addition to the TTC_TIMEOUT attribute, as some database operations may unexpectedly take longer than the value set for the TTC_TIMEOUT attribute.
Refer to "TTC_Timeout" in Oracle TimesTen In-Memory Database Reference for more information about that attribute.
You can control the per connection keep-alive settings with the following parameters:
-
TTC_TCP_KEEPALIVE_TIME_MS: The duration time (in milliseconds) between the last data packet sent and the first probe. The default is 10000 milliseconds.Note:
The Linux client platform converts this value to seconds by truncating the last three digits off of the value ofTTC_TCP_KEEPALIVE_TIME_MS. Thus, a setting of 2500 milliseconds becomes 2 seconds, instead of 2.5 seconds. -
TTC_TCP_KEEPALIVE_INTVL_MS: The time interval (in milliseconds) between subsequential probes. The default is 10000 milliseconds. -
TTC_TCP_KEEPALIVE_PROBES: The number of unacknowledged probes to send before considering the connection as failed and notifying the client. The default is set to 2 unacknowledged probes.
If you keep the default settings, then TimesTen Scaleout sends the first probe after 10 seconds (the TTC_TCP_KEEPALIVE_TIME_MS setting).
-
If there is a response, then the connection is alive and the
TTC_TCP_KEEPALIVE_TIME_MStimer is reset. -
If there is no response, then TimesTen Scaleout sends another probe after this initial probe at 10 second intervals (the
TTC_TCP_KEEPALIVE_INTVL_MSsetting). If no response is received after 2 successive probes, then this connection is aborted and TimesTen Scaleout redirects the connection to another data instance.
For example, you could modify the TCP keep alive settings in the client/server connectable to have a shorter wait time for the initial probe of 50000 milliseconds, and to check for a connection every 20000 milliseconds for a maximum number of 3 times as follows:
TTC_TCP_KEEPALIVE_TIME_MS=50000 TTC_TCP_KEEPALIVE_INTVL_MS=20000 TTC_TCP_KEEPALIVE_PROBES=3
See "TTC_TCP_KEEPALIVE_TIME_MS", "TTC_TCP_KEEPALIVE_INTVL_MS", and "TTC_TCP_KEEPALIVE_PROBES" in the Oracle TimesTen In-Memory Database Reference for more information on these connection attributes.
Managing failover for the management instances
You conduct all management activity from a single management instance, called the active management instance. However, it is highly recommended that you configure two management instances, where the standby management instance is available in case the active management instance goes down or fails.
-
If you only have a single management instance and it goes down, the databases remain operational. However, most management operations are unavailable until the management instance is restored.
-
If you configure both the active and standby management instances in your grid and only the active management instance is alive, then you can configure and manage the entire grid from this one management instance.
If both management instances are down, then:
-
You can still access all databases in the grid. However, since all management actions are requested through the active management instance, you cannot manage your grid until the active management instance is restored.
-
If data instances or their elements in the grid go down or fail, they cannot recover, restart or rejoin the grid until the active management instance is restored.
Note:
You cannot add a third management instance.As shown in Figure 11-6, all management information used by the active management instance is automatically replicated to the standby management instance. Thus, if the active management instance goes down or fails, you can promote the standby management instance to become the new active management instance through which you continue to manage the grid.
Figure 11-6 Active standby configuration for management instances
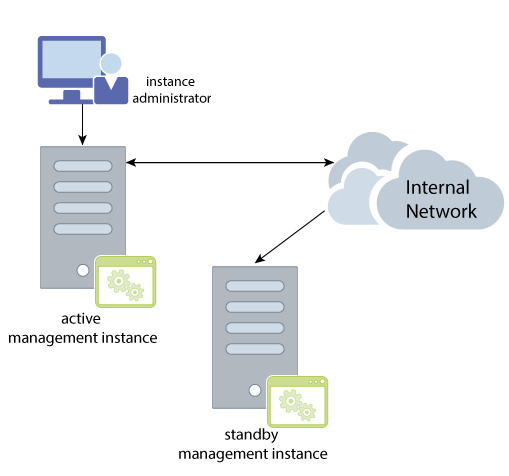
Description of ''Figure 11-6 Active standby configuration for management instances''
The following sections describes how you can manage the management instances:
Status for management instances
You use the ttGridAdmin mgmtExamine command for both the status for the management instances and to see if there are any issues that need to be resolved. This command recommends any corrective actions you can execute to fix any open issues, if necessary.
The following example shows both management instances working:
% ttGridAdmin mgmtExamine Both active and standby management instances are up. No action required. Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive ------------------------------------------------------------------------ host1 instance1 Yes Active Active 598 Up Yes host2 instance1 Yes Standby Standby 598 Up No
If one of the management instances goes down or fails, the output shows that the management instance role is Unknown and a message states that its replication agent is down. The output provides recommended commands to restart the management instance.
% ttGridAdmin mgmtExamine Active management instance is up, but standby is down Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive Message ----- --------- --------- ------------- ---------- --- -------- --------- -------- host1 instance1 Yes Active Active 600 Up No host2 instance1 No Unknown Unknown Down No Management database is not available Recommended commands: ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttGridAdmin mgmtStandbyStart
For each management instance displayed:
-
Host and Instance show the name of the management instance and the name of the host where it is located.
-
Reachable indicates whether the command was successful in reaching the management instance to determine its state.
-
RepRole(Self) indicates the recorded role, if any, known by the replication agents for replicating data between management instances. While Role(Self) indicates the recorded role known within the database for the management instances. Both of these should show the same role. If the roles are different, the
ttGridAdmin mgmtExaminecommand will try to determine the commands that would rectify the error. -
Seq is the sequence number of the most recent change on the management instance. If the
Seqvalues are the same, then the two management instances are synchronized; otherwise, the one with the largerSeqvalue has the more recent data. -
RepAgent indicates whether a replication agent is running on each management instance.
-
RepActive indicates whether changes by the
ttGridAdmin mgmtStatuscommand, which is invoked internally by thettGridAdmin mgmtExaminecommand, to management data on the management instance were successful. -
Message provides any further information about the management instance.
See "Examine management instances (mgmtExamine)" in the Oracle TimesTen In-Memory Database Reference for more details.
Starting, stopping and switching management instances
Most ttGridAdmin commands are executed through the active management instance. However, when you manage recovery for an active management instance, you may be required to execute ttGridAdmin commands on the standby management instance.
When starting, stopping, or promoting a standby management instance:
-
You can execute the
ttGridAdmin mgmtStandbyStopcommand on either management instance. The grid knows where the standby management instance is and stops it. -
You must execute the
ttGridAdmin mgmtStandbyStartcommand on the management instance that you wish to become the standby management instance. ThettGridAdmin mgmtStandbyStartcommand assumes that you want the current instance to become the standby management instance. -
If the active management instance is down, you must execute the
ttGridAdmin mgmtActiveSwitchcommand on the standby management instance to promote it to be the active management instance.
For those commands that require you to execute commands on the standby management instance, remember to set the environment with the ttenv script (as described in "Creating the initial management instance") after you log onto the host and before you execute the ttGridAdmin utility.
Active management instance failure
You should re-activate an active management instance after a failure as soon as possible to make sure that everything continues to run as expected.
Single management instance fails
While it is not recommended, you can manage the grid with a single active management instance with no standby management instance. If the single active management instance fails and recovers, re-activate the active management instance as follows:
-
Verify that there is only one management instance acting as the active management instance and that it has failed with the
ttGridAdmin mgmtExaminecommand:% ttGridAdmin mgmtExamine The only defined management instance is down. Start it. Recommendation: define a second management instance Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive ------------------------------------------------------------------------- host1 instance1 No Unknown Unknown Down No Recommended commands: ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttDaemonAdmin -start
-
After determining the reason for the failure and resolving that issue, execute the
ttGridAdmin mgmtActiveStartcommand to re-activate the active management instance.% ttGridAdmin mgmtActiveStart This management instance is now the active
-
Re-execute the
ttGridAdmin mgmtExaminecommand to verify that the active management instance is up. Follow any commands it displays if the management instance is not up.
Active management instance fails
If the active management instance fails, then you can no longer execute ttGridAdmin commands on it.
-
Promote the standby management instance on the
host2host to be the new active management instance. -
Create a new standby management instance by either:
-
Recovering the failed management instance on
host1up as the new standby management instance. This causes the new active management instance to replicate all management information to the new standby management instance. -
Deleting the failed active management instance if the failed management instance has permanently failed, then creating a new standby management instance.
-
For example, your environment has two management instances where the active management instance is on host1 and the standby management instance is on host2. Then, if the active management instance on host1 fails, then you can no longer execute ttGridAdmin commands on it. As shown in Figure 11-7, you must promote the standby management instance on host2 to become the new active management instance.
-
Log in to the
host2host on which the standby management instance exists and set the environment with thettenvscript (as described in "Creating the initial management instance") on the host with the standby management instance. -
Execute the
ttGridAdmin mgmtActiveSwitchcommand on the standby management instance. TimesTen promotes the standby management instance into the new active management instance. You can now continue to manage your grid with the new active management instance.% ttGridAdmin mgmtActiveSwitch This is now the active management instance
-
Verify that the old standby management instance is now the new active management instance with the
ttGridAdmin mgmtExaminecommand:% ttGridAdmin mgmtExamine Active management instance is up, but standby is down Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive ------------------------------------------------------------------------- host2 instance1 Yes Active Active 622 Up Yes host1 instance1 No Unknown Unknown Down No Management database is not available Recommended commands: ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttGridAdmin mgmtStandbyStart
Once the new active management instance is processing requests, ensure that a new standby management instance is created by one of the following methods:
Failed management instance can be recovered
If the failed active management instance can be recovered, you need to perform the following tasks:
Figure 11-8 The failed management instance can be recovered
Description of ''Figure 11-8 The failed management instance can be recovered''
-
If you can recover the failed management instance, as shown in Figure 11-8, then bring back up the failed host on which the old active management instance existed. Then, execute the
ttGridAdmin mgmtStandbyStartcommand on this host, which re-initiates the management instance as the new standby management instance. It also re-creates the active standby configuration between the new active and standby management instances and replicates all management information on the active management instance to the standby management instance.% ttGridAdmin mgmtStandbyStart Standby management instance started
-
Verify that the active and standby management instances are as expected in their new roles with the
ttGridAdmin mgmtExaminecommand:% ttGridAdmin mgmtExamine Both active and standby management instances are up. No action required. Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive ------------------------------------------------------------------------- host2 instance1 Yes Active Active 603 Up Yes host1 instance1 Yes Standby Standby 603 Up No
Failed management instance encounters a permanent failure
If the failed active management instance has failed permanently, you need to perform the following tasks:
Figure 11-9 The active management instance fails permanently
Description of ''Figure 11-9 The active management instance fails permanently''
-
Remove the permanently failed active management instance from the model with the
ttGridAdmin instanceDeletecommand.% ttGridAdmin instanceDelete host1.instance1 Instance instance1 on Host host1 deleted from Model
Note:
If there are no other instances on the host where the failed active management instance existed, you may want to delete the host and the installation. -
Add a new standby management instance with its supporting host and installation to the model.
% ttGridAdmin hostCreate host9 -address host9.example.com Host host9 created in Model % ttGridAdmin installationCreate -host host9 -location /timesten/host9/installation1 Installation installation1 on Host host9 created in Model % ttGridAdmin instanceCreate -host host9 -location /timesten/host9 -type management Instance instance1 on Host host9 created in Model
-
Apply the configuration changes to remove the failed active management instance and add in a new standby management instance to the grid by executing the
ttGridAdmin modelApplycommand.% ttGridAdmin modelApply Copying Model.........................................................OK Exporting Model Version 2.............................................OK Unconfiguring standby management instance.............................OK Marking objects 'Pending Deletion'....................................OK Stop any Instances that are 'Pending Deletion'........................OK Deleting any Instances that are 'Pending Deletion'....................OK Deleting any Hosts that are no longer in use..........................OK Verifying Installations...............................................OK Creating any missing Installations....................................OK Creating any missing Instances........................................OK Adding new Objects to Grid State......................................OK Configuring grid authentication.......................................OK Pushing new configuration files to each Instance......................OK Making Model Version 2 current........................................OK Making Model Version 3 writable.......................................OK Checking ssh connectivity of new Instances............................OK Starting new management instance......................................OK Configuring standby management instance...............................OK Starting new data instances...........................................OK ttGridAdmin modelApply complete
The
ttGridAdmin modelApplycommand initiates the active standby configuration between the active and standby management instances and replicates the management information on the active management instance to the standby management instance. -
Verify that the active and standby management instances are as expected in their new roles with the
ttGridAdmin mgmtExaminecommand:% ttGridAdmin mgmtExamine Both active and standby management instances are up. No action required. Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive ------------------------------------------------------------------------- host2 instance1 Yes Active Active 603 Up Yes host9 instance1 Yes Standby Standby 603 Up No
Standby management instance failure
How you re-activate the standby management instance depends on the type of failure as described in the following sections:
Standby management instance recovers
If the standby management instance recovers, then:
-
Check the status with the
ttGridAdmin mgmtExaminecommand:% ttGridAdmin mgmtExamine Active management instance is up, but standby is down Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive Message ----------------------------------------------------------------------------- host1 instance1 Yes Active Active 605 Up No host2 instance1 No Unknown Unknown Down No Management database is not available Recommended commands: ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttGridAdmin mgmtStandbyStart
-
Log into the host with the standby management instance. If you have not done so already, set the environment with the
ttenvscript (as described in "Creating the initial management instance"). -
Once you bring the failed management instance back up, then execute the
ttGridAdmin mgmtStandbyStartcommand on the host with the standby management instance.% ttGridAdmin mgmtStandbyStart Standby management instance started
This command re-integrates the standby management instance in your grid, initiates the active standby configuration between the active and standby management instances and replicates all management information on the active management instance to the standby management instance.
Standby management instance experiences permanent failure
If the standby management instance has permanently failed, perform the following commands:
-
Delete the failed standby management instance on the
host2host. -
Create a new standby management instance on the
host9host to take over the duties of the failed standby management instance. Then, the active management instance replicates the management information to the new standby management instance.
Figure 11-10 The standby management instance fails permanently

Description of ''Figure 11-10 The standby management instance fails permanently''
-
Remove the permanently failed standby management instance from the model with the
ttGridAdmin instanceDeletecommand.% ttGridAdmin instanceDelete host2.instance1 Instance instance1 on Host host2 deleted from Model
Note:
If there are no other instances on the host where the failed management instance existed, you may want to delete the host and the installation. -
Add a new standby management instance with its supporting host and installation to the model.
% ttGridAdmin hostCreate host9 -address host9.example.com Host host9 created in Model % ttGridAdmin installationCreate -host host9 -location /timesten/host9/installation1 Installation installation1 on Host host9 created in Model % ttGridAdmin instanceCreate -host host9 -location /timesten/host9 -type management Instance instance1 on Host host9 created in Model
-
Apply the configuration changes to remove the failed standby management instance and add in a new standby management instance to the grid by executing the
ttGridAdmin modelApplycommand, as shown in "Applying the changes made to the model."% ttGridAdmin modelApply Copying Model.........................................................OK Exporting Model Version 9.............................................OK Unconfiguring standby management instance.............................OK Marking objects 'Pending Deletion'....................................OK Stop any Instances that are 'Pending Deletion'........................OK Deleting any Instances that are 'Pending Deletion'....................OK Deleting any Hosts that are no longer in use..........................OK Verifying Installations...............................................OK Creating any missing Instances........................................OK Adding new Objects to Grid State......................................OK Configuring grid authentication.......................................OK Pushing new configuration files to each Instance......................OK Making Model Version 9 current........................................OK Making Model Version 10 writable......................................OK Checking ssh connectivity of new Instances............................OK Starting new management instance......................................OK Configuring standby management instance...............................OK Starting new data instances...........................................OK ttGridAdmin modelApply complete
The
ttGridAdmin modelApplycommand initiates the active standby configuration between the active and standby management instances and replicates the management information on the active management instance to the standby management instance.
Both management instances fail
You must restart the management instances to return the grid to its full functionality and to be able to manage the grid through the active management instance.
If both of the management instances are down, you need to discover which management instance has the latest changes on it to decide which management instance is to become the new active management instance.
Note:
If both management instances fail permanently, call Oracle Support.The following describes the methods to perform when both management instances are down:
Bring back both management instances
If you can bring back both management instances:
Note:
If you have not done so already, set the environment with thettenv script (as described in "Creating the initial management instance").-
Execute the
ttGridAdmin mgmtExaminecommand on one of the management instances to discover which is the appropriate one to become the active management instance. ThettGridAdmin mgmtExaminecommand evaluates both management instances and prints out the highest sequence number for the management instance that has more management data. It is this management instance that should be re-activated as the active management instance.% ttGridAdmin mgmtExamine One or more management instance is down. Start them and run mgmtExamine again. Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive Message ------------------------------------------------------------------------------ host1 instance1 No Unknown Unknown Down No Management database is not available host2 instance1 No Unknown Unknown Down No Management database is not available Recommended commands: ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttDaemonAdmin -start -force ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttDaemonAdmin -start -force sleep 30 /timesten/host1/instance1/bin/ttenv ttGridAdmin mgmtExamine
-
Execute the recommended commands listed by the
ttGridAdmin mgmtExaminecommand. The commands for this example result in restarting the daemons for each management instance:% ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttDaemonAdmin -start -force TimesTen Daemon (PID: 3858, port: 11000) startup OK. % ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttDaemonAdmin -start -force TimesTen Daemon (PID: 4052, port: 12000) startup OK.
-
Re-execute the
ttGridAdmin mgmtExaminecommand to verify that both management instances are up. If either of the management instances are not up, then thettGridAdmin mgmtExaminecommand may suggest another set of commands to run.In this example, the second invocation of the
ttGridAdmin mgmtExaminecommand shows that the management instances are not up. Thus, this example shows that the command next requests that you:-
Stop the main daemon of the data instance for both management instances.
-
Execute the
ttGridAdmin mgmtActiveStartcommand on the management instance with the higher sequence number provided by thettGridAdmin mgmtExaminecommand. This re-activates the active management instance. -
Execute the
ttGridAdmin mgmtStandbyStartcommand on the management instance that you want to act as the standby management instance. This command assigns the other management instance as the standby management instance in TimesTen Scaleout, initiates the active standby configuration between the active and standby management instances and synchronizes the management information on the active management instance to the standby management instance.
% ttGridAdmin mgmtExamine Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive Message ------------------------------------------------------------------------ host1 instance1 Yes Active Active 581 Down No host2 instance1 Yes Standby Standby 567 Down No Recommended commands: ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttDaemonAdmin -stop ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttDaemonAdmin -stop sleep 30 ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttGridAdmin mgmtActiveStart sleep 30 ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttGridAdmin mgmtStandbyStart
Executing these commands restarts both the active and standby management instances:
% ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttDaemonAdmin -stop TimesTen Daemon (PID: 3858, port: 11000) stopped. % ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttDaemonAdmin -stop TimesTen Daemon (PID: 3859, port: 12000) stopped. % ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host1.example.com /timesten/host1/instance1/bin/ttenv ttGridAdmin mgmtActiveStart This management instance is now the active % ssh -o StrictHostKeyChecking=yes -o PasswordAuthentication=no -x host2.example.com /timesten/host2/instance1/bin/ttenv ttGridAdmin mgmtStandbyStart Standby management instance started
Continue to re-execute the
ttGridAdmin mgmtExaminecommand until you receive the message that both management instances are up.% ttGridAdmin mgmtExamine Both active and standby management instances are up. No action required. Host Instance Reachable RepRole(Self) Role(Self) Seq RepAgent RepActive Message ---------------------------------------------------------------------- host1 instance1 Yes Active Active 567 Up Yes host2 instance1 Yes Standby Standby 567 Up No -
Bring back one of the management instances
As soon as you notice that your standby management instance is down, it is important that you recreate it as soon as possible. If not, then your grid topology may be dramatically different than it was before if your active management instance also goes down. That is, if the active management instance goes down or fails in such a way that the best option is to bring back up the standby management instance that has been down for a while, then this may result in an incorrect grid topology as follows:
-
If you had recently added instances to your grid, they may be gone.
-
If you had recently deleted instances from your grid, they may be back.
-
If you had recently created databases, they may have been deleted.
-
If you had recently destroyed databases, they might be recreated.
If you can bring back only one of the management instances, re-activate this instance as the active management instance. The following example assumes that the management instance on the host2 host is down and the management instance on the host1 host was able to be brought back.
-
Execute the
ttGridAdmin mgmtActiveStartcommand on the management instance onhost1. This re-activates as the active management instance.% ttGridAdmin mgmtActiveStart This management instance is now the active
-
Remove the permanently failed standby management instance from the model with the
ttGridAdmin instanceDeletecommand.% ttGridAdmin instanceDelete host2.instance1 Instance instance1 on Host host2 deleted from Model
Note:
If there are no other instances on the host where the down management instance existed, you may want to delete the host and the installation. -
Add a new standby management instance with its supporting host and installation to the model.
% ttGridAdmin hostCreate host9 -address host9.example.com Host host9 created in Model % ttGridAdmin installationCreate -host host9 -location /timesten/host9/installation1 Installation installation1 on Host host9 created in Model % ttGridAdmin instanceCreate -host host9 -location /timesten/host9 -type management Instance instance1 on Host host9 created in Model
-
Apply the configuration changes to remove the failed standby management instance and add in a new standby management instance to the grid by executing the
ttGridAdmin modelApplycommand.% ttGridAdmin modelApply Copying Model.........................................................OK Exporting Model Version 9.............................................OK Unconfiguring standby management instance.............................OK Marking objects 'Pending Deletion'....................................OK Stop any Instances that are 'Pending Deletion'........................OK Deleting any Instances that are 'Pending Deletion'....................OK Deleting any Hosts that are no longer in use..........................OK Verifying Installations...............................................OK Creating any missing Instances........................................OK Adding new Objects to Grid State......................................OK Configuring grid authentication.......................................OK Pushing new configuration files to each Instance......................OK Making Model Version 9 current........................................OK Making Model Version 10 writable......................................OK Checking ssh connectivity of new Instances............................OK Starting new management instance......................................OK Configuring standby management instance...............................OK Starting new data instances...........................................OK ttGridAdmin modelApply complete
The
ttGridAdmin modelApplycommand initiates the active standby configuration between the active and standby management instances and replicates the management information on the active management instance to the standby management instance.
Performance recommendations
Enhance your performance by setting a timeout for the channel create.
Set a timeout for create channel requests
Each element communicates over channels to all other elements. However, if any request to create a channel between elements hangs due to software issues or network failures, then all channel create requests could be blocked. Since open channels are required for element communication, we need to detect any hangs within the channel creation process.
You can set a timeout (in milliseconds) to wait for a response to a channel create request to a remote element with the ChannelCreateTimeout general connection attribute. See "ChannelCreateTimeout" in the Oracle TimesTen In-Memory Database Reference for full details.