Specifying System Accreditation Range-Related Constants
Following the specification of each classification in the user accreditation range, a number of system accreditation range-related system constants are specified with the keywords minimum clearance=, minimum sensitivity label=, and minimum protect as classification=, as described below.
The Minimum Clearance= Keyword
Following the user accreditation range specifications is the minimum clearance= keyword. This keyword is followed by a specification of the minimum clearance of any user on the system. This minimum clearance will be enforced by the system when setting user's clearances. The clearance is taken to begin with the first non-blank character following the blank after the keyword, and continues up to the next semicolon or the end of the line. The clearance must be well formed and in canonical form. A clearance is in canonical form if it begins with the sname of a classification followed by the name of zero or more CLEARANCES: WORDS:, in the order in which the words appear in the CLEARANCES: section. This clearance must be valid according to the CLEARANCES: encodings, but does not have to conform to the clearance combination constraints (and is therefore not well formed), and does not have to be in the user accreditation range.
The Minimum Sensitivity Label= Keyword
Following the minimum clearance= keyword is the minimum sensitivity label= keyword. This keyword is followed by a specification of the minimum sensitivity label to be used on the system. This minimum sensitivity label forms the low end of the system accreditation range, and will be enforced by the system when setting sensitivity labels. The sensitivity label is taken to begin with the first non-blank character following the blank after the keyword, and continues up to the next semicolon or the end of the line. The sensitivity label must be well formed and in canonical form. A sensitivity label is in canonical form if it begins with the sname of a classification followed by the name of zero or more SENSITIVITY LABELS: WORDS:, in the order in which the words appear in the SENSITIVITY LABELS: section. The minimum sensitivity label does not have to be in the user accreditation range. However, the minimum sensitivity label must be dominated by the minimum clearance.
The Minimum Protect As Classification= Keyword
Following the minimum sensitivity label= keyword is the minimum protect as classification= keyword. Following this keyword is the minimum classification at which all system output is to be protected unless it is manually reviewed and downgraded. The classification name is taken to begin with the first non-blank character following the blank after the keyword, and continues up to the next semicolon or the end of the line. The name specified must match either the short, long, or alternate name of one of the classifications specified in the classifications section of the encodings file. The minimum protect as classification cannot be greater than the classification in the minimum clearance.
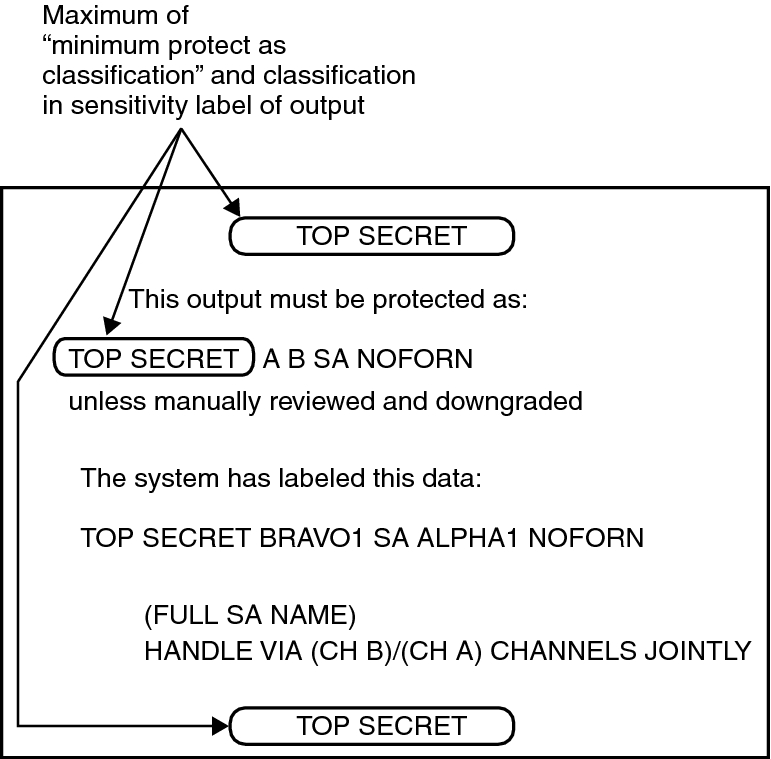
Printer Banner Example Denoting Minimum Protect As Classification Usage is an example of how the minimum protect as classification will be used by the system when producing printed output. The system puts the maximum of the minimum protect as classification and the classification in the sensitivity label of the data being printed at the top and bottom of the banner page, and in the warning statement about how the output must be protected.
Figure 5 Printer Banner Example Denoting Minimum Protect As Classification Usage