正向和逆向 FFT 例程
以下各表列出了 FFT 例程的名称及其调用序列。 双精度例程名称位于方括号中。有关数据类型和参数大小的详细信息,请参见各手册页。
|
|
Oracle Developer Studio 性能库 FFT 例程使用以下参数。
OPT:此标志指示是调用例程来初始化变换还是来计算变换。
N1、N2、N3:一维、二维和三维变换的问题维。
X:输入数组,如果例程是复数到复数变换或复数到实数变换,则 X 的类型是 COMPLEX。对于实数到复数变换,X 的类型是 REAL。
Y:输出数组,如果例程是复数到复数变换或实数到复数变换,则 Y 的类型是 COMPLEX。对于复数到实数变换,Y 的类型是 REAL。
LDX1、LDX2 和 LDY1、LDY2:LDX1 和 LDX2 是输入数组的主维,LDY1 和 LDY2 是输出数组的主维。FFT 例程允许输出覆盖输入,这是场内变换,或允许输出存储在除输入数组以外的另一个数组中,这是场外变换。在复数到复数变换中,输入数据的大小与输出数据相同。然而,实数到复数变换以及复数到实数变换对输入数据和输出数据有不同的内存要求。在计算场内变换时必须谨慎,应确保输入数组足够大,以容纳变换结果。
TRIGS:包含三角权重的数组。
IFAC:包含问题维的因子的数组。问题大小如下:
线性 FFT:维 N1 的问题大小
二维 FFT:维 N1 和 N2 的问题大小
三维 FFT:维 N1、N2 和 N3 的问题大小
虽然 N1、N2 和 N3 可以是任意大小,但在以下情况下,可以最有效地计算实数到复数变换或复数到实数变换:
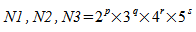 ,
,在以下情况下,可以最有效地计算复数到复数变换:
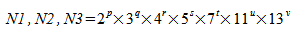 ,
,其中 p、q、r、s、t、u 和 v 是整数,且 p、q、r、s、t、u、v ≥ 0。
-
WORK:工作区,其大小取决于例程以及用于计算变换的线程数量(如果该例程已并行化)。
-
LWORK:工作区的大小。如果 LWORK 是零,例程将分配具有所需大小的工作区。
-
SCALE:对输出进行缩放的一个标量。有时,对于一维变换,使用 1/N1 的比例因子定义逆变换,对二维变换使用 1/(N1 × N2),对三维变换使用 1/(N1 × N2 × N3)。在这种情况下,我们说对逆变换进行了归一化处理。如果归一化的 FFT 之后是逆向 FFT,结果就是原始的输入数据。Oracle Developer Studio 性能库 FFT 例程没有进行归一化处理。不过,通过使用存储在 SCALE 中的合适比例因子调用逆向 FFT 例程,可以很容易地进行归一化处理。
-
ERR:如果在例程中遇到错误,该标志将返回非零值,否则返回零。
线性 FFT 例程
线性 FFT 例程仅计算一维的实数或复数数据的 FFT。这些数据可以是一个或多个复数或实数序列。对于单一序列,数据将存储在向量中。如果要转换多个序列,则这些序列将逐列存储在二维数组中,并沿列方向计算每个序列的一维 FFT。线性正向 FFT 例程计算:
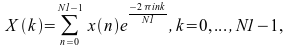 其中
其中
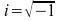 。
。
通过正变换,如果输入是大小为 N1 的一个或多个复数序列,结果将是一个或多个复数序列,每个序列由 N1 个不相关的数据点组成。 然而,如果输入是一个或多个实数序列,每个序列包含 N1 个实数数据点,则结果将是共轭对称的一个或多个复数序列。 即:
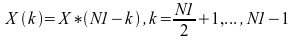
X(0) 的虚部始终为零。如果 N1 是偶数,
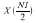 也为零。将显式存储两个零。因为可从每个序列的前半部分得到后半部分,所以仅计算
也为零。将显式存储两个零。因为可从每个序列的前半部分得到后半部分,所以仅计算
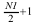 复数数据点并将其存储在输出数组中。在本章此处和其他地方,将对整数除法进行向下舍入。
复数数据点并将其存储在输出数组中。在本章此处和其他地方,将对整数除法进行向下舍入。
通过逆变换,如果要计算 N1 点复数到复数变换,则每个输入序列中应当有 N1 个不相关数据点,并在输出数组中返回 N1 个数据点。然而,如果要计算 N1 点复数到实数变换,则输入中只应当有每个共轭对称输入序列的前 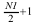 个复数数据点,例程将在每个输出序列中返回 N1 个实数数据点。
个复数数据点,例程将在每个输出序列中返回 N1 个实数数据点。
对于 N1 的每个值,在计算实际 FFT 之前,必须调用正向或逆向例程来计算 N1 的因子以及与这些因子关联的三角权重。只要 N1 保持不变,就可以在后续变换中重用这些因子和三角权重。
下面的表 12列出了单精度线性 FFT 例程及其用途。对于使用二维数组作为输入和输出的例程,表 12还列出了主维要求。这些信息同样适用于相应的双精度例程,只是其数据类型是双精度和双精度复数。有关映射,请参见表 12。有关例程及其参数的完整说明,请参见各手册页。
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
注 - 请注意以下有关表 12的信息:
-
LDX1 是输入数组的主维。
-
LDY1 是输出数组的主维。
-
N1 是 FFT 问题的第一个维。
-
N2 是 FFT 问题的第二个维。
-
使用 OPT = 0 调用例程以初始化例程时,唯一进行的错误检查是确定是否 N1 < 0
以下示例说明了如何计算一组序列的线性实数到复数和复数到实数 FFT。
示例 10 线性实数到复数 FFT 和复数到实数 FFTmy_system% cat testscm.f
PROGRAM TESTSCM
IMPLICIT NONE
INTEGER :: LW, IERR, I, J, K, LDX, LDC
INTEGER,PARAMETER :: N1 = 3, N2 = 2, LDZ = N1,
$ LDC = N1, LDX = 2*LDC
INTEGER, DIMENSION(:) :: IFAC(128)
REAL :: SCALE
REAL, PARAMETER :: ONE = 1.0
REAL, DIMENSION(:) :: SW(N1), TRIGS(2*N1)
REAL, DIMENSION(0:LDX-1,0:N2-1) :: X, V, Y
COMPLEX, DIMENSION(0:LDZ-1, 0:N2-1) :: Z
* workspace size
LW = N1
SCALE = ONE/N1
WRITE(*,*)
$ 'Linear complex-to-real and real-to-complex FFT of a sequence'
WRITE(*,*)
X = RESHAPE(SOURCE = (/.1, .2, .3,0.0,0.0,0.0,7.,8.,9.,
$ 0.0, 0.0, 0.0/), SHAPE=(/6,2/))
V = X
WRITE(*,*) 'X = '
DO I = 0,N1-1
WRITE(*,'(2(F4.1,2x))') (X(I,J), J = 0, N2-1)
END DO
WRITE(*,*)
* intialize trig table and compute factors of N1
CALL SFFTCM(0, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
CALL SFFTCM(-1, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
$ SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Z ='
DO I = 0, N1/2
WRITE(*,'(2(A1, F4.1,A1,F4.1,A1,2x))') ('(',REAL(Z(I,J)),
$ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place forward linear FFT.
* X must be large enough to store N1/2+1 complex values
CALL SFFTCM(-1, N1, N2, ONE, X, LDX, X, LDC, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, X, LDC, N2)
WRITE(*,*)
* Compute out-of-place inverse linear FFT.
CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, X, LDX, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'out-of-place inverse FFT of Z:'
DO I = 0, N1-1
WRITE(*,'(2(F4.1,2X))') (X(I,J), J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place inverse linear FFT.
CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, Z, LDZ*2, TRIGS,
$ IFAC, SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place inverse FFT of Z:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Z, LDZ*2, N2)
WRITE(*,*)
END PROGRAM TESTSCM
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F4.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F4.1,A1,F4.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testscm.f -xlibrary=sunperf
my_system% a.out
Linear complex-to-real and real-to-complex FFT of a sequence
X =
0.1 7.0
0.2 8.0
0.3 9.0
out-of-place forward FFT of X:
Z =
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
in-place forward FFT of X:
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
out-of-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
in-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
示例 7-1 说明:
X 的正向 FFT 实际上是:
由于对称性,Z(2) 是 Z(1) 的共轭复数,因此仅存储前两个
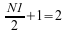 复数值。对于场内正变换,将使用实数数组 X 作为输入和输出来调用 SFFTCM。因为 SFFTCM 要求输出数组的类型为 COMPLEX,所以作为输出数组的 X 的主维必须就像 X 是复数那样。由于实数数组 X 的主维是 LDX = 2 × LDC,因此作为复数输出数组的 X 的主维必须是 LDC。同样,对于场内逆变换,将使用复数数组 Z 作为输入和输出来调用 CFFTSM。因为 CFFTSM 要求输出数组的类型为 REAL,所以作为输出数组的 Z 的主维必须就像 Z 是实数那样。由于复数数组 Z 的主维是 LDZ,因此作为实数输出数组的 Z 的主维必须是 LDZ × 2。
复数值。对于场内正变换,将使用实数数组 X 作为输入和输出来调用 SFFTCM。因为 SFFTCM 要求输出数组的类型为 COMPLEX,所以作为输出数组的 X 的主维必须就像 X 是复数那样。由于实数数组 X 的主维是 LDX = 2 × LDC,因此作为复数输出数组的 X 的主维必须是 LDC。同样,对于场内逆变换,将使用复数数组 Z 作为输入和输出来调用 CFFTSM。因为 CFFTSM 要求输出数组的类型为 REAL,所以作为输出数组的 Z 的主维必须就像 Z 是实数那样。由于复数数组 Z 的主维是 LDZ,因此作为实数输出数组的 Z 的主维必须是 LDZ × 2。
以下示例示例 11说明了如何计算一组序列的线性复数到复数 FFT。
示例 11 线性复数到复数 FFTmy_system% cat testccm.f
PROGRAM TESTCCM
IMPLICIT NONE
INTEGER :: LDX1, LDY1, LW, IERR, I, J, K, LDZ1, NCPUS,
$ USING_THREADS, IFAC(128)
INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1, LDZ1 = N1,
$ LDY1 = N1+2
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/N1
COMPLEX :: Z(0:LDZ1-1,0:N2-1), X(0:LDX1-1,0:N2-1),
$ Y(0:LDY1-1,0:N2-1)
REAL :: TRIGS(2*N1)
REAL, DIMENSION(:), ALLOCATABLE :: SW
* get number of threads
NCPUS = USING_THREADS()
* workspace size
LW = 2 * N1 * NCPUS
WRITE(*,*)'Linear complex-to-complex FFT of one or more sequences'
WRITE(*,*)
ALLOCATE(SW(LW))
X = RESHAPE(SOURCE =(/(.1,.2),(.3,.4),(.5,.6),(.7,.8),(.9,1.0),
$ (1.1,1.2),(1.3,1.4),(1.5,1.6),(1.7,1.8),(1.9,2.0),(2.1,2.2),
$ (1.2,2.0)/), SHAPE=(/LDX1,N2/))
Z = X
WRITE(*,*) 'X = '
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(X(I,J)),
$ ',',AIMAG(X(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)* intialize trig table and compute factors of N1
CALL CFFTCM(0, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
CALL CFFTCM(-1, N1, N2, ONE, X, LDX1, Y, LDY1, TRIGS, IFAC,
$ SW, 0, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
* Compute in-place forward linear FFT. LDZ1 must equal LDX1
CALL CFFTCM(-1, N1, N2, ONE, Z, LDX1, Z, LDZ1, TRIGS,
$ IFAC, SW, 0, IERR)
WRITE(*,*) 'in-place forward FFT of X:'
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Z(I,J)),
$ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*) 'Y ='
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
END DO
WRITE(*,*)
* Compute in-place inverse linear FFT.
CALL CFFTCM(1, N1, N2, SCALE, Y, LDY1, Y, LDY1, TRIGS, IFAC,
$ SW, LW, IERR)
IF (IERR .NE. 0) THEN
PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
STOP
END IF
WRITE(*,*) 'in-place inverse FFT of Y:'
WRITE(*,*) 'Y ='
DO I = 0, N1-1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
END DO
DEALLOCATE(SW)
END PROGRAM TESTCCM
my_system% f95 -dalign testccm.f -library=sunperf
my_system% a.out
Linear complex-to-complex FFT of one or more sequences
X =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
in-place forward FFT of X:
( 0.9, 1.2) ( 2.7, 3.0) ( 4.5, 4.8) ( 5.2, 6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1, 0.7)
out-of-place forward FFT of X:
Y =
( 0.9, 1.2) ( 2.7, 3.0) ( 4.5, 4.8) ( 5.2, 6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1, 0.7)
in-place inverse FFT of Y:
Y =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
二维 FFT 例程
对于线性 FFT 例程,如果输入是一个二维数组,则将仅沿着一个维计算 FFT,也就是沿着数组的列。二维 FFT 例程将二维数组作为输入,并同时沿着列和行维计算 FFT。具体来说,正向二维 FFT 例程计算如下:
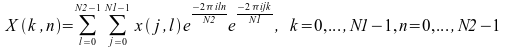
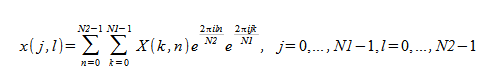
对于正向和逆向二维变换,输入问题是 N1 × N2 的复数到复数变换产生的复数数组也是 N1 × N2。
在计算实数到复数二维变换(正向 FFT)时,如果实数输入数组的维是 N1 × N2,则结果将是一个复数数组,且维数是
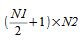 。
。
相反,在计算维是 N1 × N2 的复数到实数变换(逆向 FFT)时,需要一个
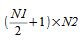 复数数组作为输入。与实数到复数及复数到实数线性 FFT 一样,由于共轭对称性,只有前
复数数组作为输入。与实数到复数及复数到实数线性 FFT 一样,由于共轭对称性,只有前
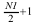 个复数数据点需要沿着第一个维存储在输入或输出数组中。复数子数组
个复数数据点需要沿着第一个维存储在输入或输出数组中。复数子数组
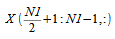 可通过
可通过
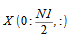 如下所示:
如下所示:
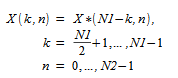
要计算二维变换,必须调用两次 FFT 例程。第一次调用对例程进行初始化,第二次调用实际对变换进行计算。初始化包括计算 N1 和 N2 的因子以及与这些因子关联的三角权重。在后续的正向或逆向变换中,只要 N1 和 N2 保持不变,就不必进行初始化了。
重要信息:从二维 FFT 例程返回时,Y(0 : N - 1, :) 将包含变换结果,并且 Y(N : LDY-1, :) 的原始内容将被覆盖。此处,在复数到复数和复数到实数变换中,N = N1;在实数到复数变换中,N =
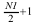 。
。
下面的表 13列出了单精度二维 FFT 例程及其用途。这些信息同样适用于相应的双精度例程,只是其数据类型是双精度和双精度复数。有关映射,请参见表 13。有关例程及其参数的完整说明,请参阅各手册页。
| ||||||||||||||||||||||||||||||||||||||||||||||||
注 - 请注意以下有关表 13的信息
-
LDX1 是输入数组的主维。
-
LDY1 是输出数组的主维。
-
N1 是 FFT 问题的第一个维。
-
N2 是 FFT 问题的第二个维。
-
使用 OPT = 0 调用例程以初始化例程时,唯一进行的错误检查是确定是否 N1、N2 < 0。
以下示例说明了如何计算二维数组的二维实数到复数 FFT 和复数到实数 FFT。
my_system% cat testsc2.f
PROGRAM TESTSC2
IMPLICIT NONE
INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1,
$ LDY1 = N1/2+1, LDR1 = 2*(N1/2+1)
INTEGER LW, IERR, I, J, K, IFAC(128*2)
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2)
REAL :: V(LDR1,N2), X(LDX1, N2), Z(LDR1,N2),
$ SW(2*N2), TRIGS(2*(N1+N2))
COMPLEX :: Y(LDY1,N2)
WRITE(*,*) $'Two-dimensional complex-to-real and real-to-complex FFT'
WRITE(*,*)
X = RESHAPE(SOURCE = (/.1, .2, .3, .4, .5, .6, .7, .8,
$ 2.0,1.0, 1.1, 1.2/), SHAPE=(/LDX1,N2/))
DO I = 1, N2
V(1:N1,I) = X(1:N1,I)
END DO
WRITE(*,*) 'X ='
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (X(I,J), J = 1, N2)
END DO
WRITE(*,*)
* Initialize trig table and get factors of N1, N2
CALL SFFTC2(0,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
$ IFAC,SW,0,IERR)
* Compute 2-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform in X because LDX1 < 2*(N1/2+1)
CALL SFFTC2(-1,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Y ='
DO I = 1, N1/2+1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J)),
$ ',',AIMAG(Y(I,J)),')', J = 1, N2)
END DO
WRITE(*,*)
* Compute 2-dimensional in-place forward FFT.
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
CALL SFFTC2(-1,N1,N2,ONE,V,LDR1,V,LDR1/2,TRIGS,
$ IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, V, LDR1/2, N2)
* Compute 2-dimensional out-of-place inverse FFT.
* Leading dimension of Z must be even
CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Z,LDR1,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place inverse FFT of Y:'
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (Z(I,J), J = 1, N2)
END DO
WRITE(*,*)
* Compute 2-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Y,2*LDY1,
$ TRIGS,IFAC,SW,0,IERR)
WRITE(*,*) 'in-place inverse FFT of Y:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Y, 2*LDY1, N2)
END PROGRAM TESTSC2
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testsc2.f -library=sunperf
my_system% a.out
Two-dimensional complex-to-real and real-to-complex FFT
x =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
out-of-place forward FFT of X:
Y =
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
in-place forward FFT of X:
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
三维 FFT 例程
Oracle Developer Studio 性能库包括了用于计算三维 FFT 的例程。在这种情况下,将沿着三维数组的所有三个维计算 FFT。正向 FFT 计算
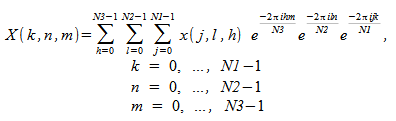 ,
,
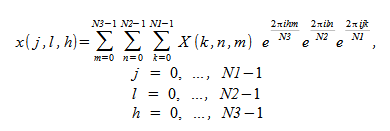
在复数到复数变换中,如果输入问题是 N1 × N2 × N3,则三维变换产生的复数数组也是 N1 × N2 × N3。 在计算实数到复数三维变换时,如果实数输入数组的维数是 N1 × N2 × N3,则结果将是一个复数数组,且维数是
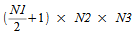 相反,在计算维数是 N1 × N2 × N3 的复数到实数 FFT 时,
相反,在计算维数是 N1 × N2 × N3 的复数到实数 FFT 时,
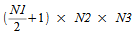 复数数组作为输入。与实数到复数及复数到实数线性 FFT 一样,由于共轭对称性,只有前
复数数组作为输入。与实数到复数及复数到实数线性 FFT 一样,由于共轭对称性,只有前
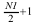 个复数数据点需要沿着第一个维存储。复数子数组
个复数数据点需要沿着第一个维存储。复数子数组
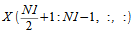 可通过
可通过
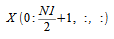 如下所示:
如下所示:
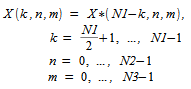
要计算三维变换,必须调用两次 FFT 例程:第一次是进行初始化,第二次是实际计算变换。初始化包括计算 N1、N2 和 N3 的因子以及与这些因子关联的三角权重。在后续的正向或逆向变换中,只要 N1、N2 和 N3 保持不变,就不必进行初始化了。
重要信息:从三维 FFT 例程返回时,Y(0 : N - 1, :, :) 将包含变换结果,并且 Y(N:LDY1-1, :, :) 的原始内容将被覆盖。此处,在复数到复数和复数到实数变换中,N = N1;在实数到复数变换中,N =
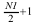 。
。
表 14列出了单精度三维 FFT 例程及其用途。这些信息同样适用于相应的双精度例程,只是其数据类型是双精度和双精度复数。有关映射,请参见表 14。有关例程及其参数的完整说明,请参见各手册页。
| ||||||||||||||||||||||||||||||||||||||||||||||||
注 - 请注意以下有关表 14的信息:
-
LDX1 是输入数组的第一个主维。
-
LDX2 是输入数组的第二个主维。
-
LDY1 是输出数组的第一个主维。
-
LDY2 是输出数组的第二个主维。
-
N1 是 FFT 问题的第一个维。
-
N2 是 FFT 问题的第二个维。
-
N3 是 FFT 问题的第三个维。
-
使用 OPT = 0 调用例程以初始化例程时,唯一进行的错误检查是确定是否 N1、N2、N3 < 0。
示例 7-4 说明了如何计算三维数组的三维实数到复数 FFT 和复数到实数 FFT。
示例 13 三维数组的三维实数到复数 FFT 和复数到实数 FFTmy_system% cat testsc3.f
PROGRAM TESTSC3
IMPLICIT NONE
INTEGER LW, NCPUS, IERR, I, J, K, USING_THREADS, IFAC(128*3)
INTEGER, PARAMETER :: N1 = 3, N2 = 4, N3 = 2, LDX1 = N1,
$ LDX2 = N2, LDY1 = N1/2+1, LDY2 = N2,
$ LDR1 = 2*(N1/2+1), LDR2 = N2
REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2*N3)
REAL :: V(LDR1,LDR2,N3), X(LDX1,LDX2,N3), Z(LDR1,LDR2,N3),
$ TRIGS(2*(N1+N2+N3))
REAL, DIMENSION(:), ALLOCATABLE :: SW
COMPLEX :: Y(LDY1,LDY2,N3)
WRITE(*,*)
$'Three-dimensional complex-to-real and real-to-complex FFT'
WRITE(*,*)
* get number of threads
NCPUS = USING_THREADS()
* compute workspace size required
LW = (MAX(MAX(N1,2*N2),2*N3) + 16*N3) * NCPUS
ALLOCATE(SW(LW))
X = RESHAPE(SOURCE =
$ (/ .1, .2, .3, .4, .5, .6, .7, .8, .9,1.0,1.1,1.2,
$ 4.1,1.2,2.3,3.4,6.5,1.6,2.7,4.8,7.9,1.0,3.1,2.2/),
$ SHAPE=(/LDX1,LDX2,N3/))
V = RESHAPE(SOURCE =
$ (/.1,.2,.3,0.,.4,.5,.6,0.,.7,.8,.9,0.,1.0,1.1,1.2,0.,
$ 4.1,1.2,2.3,0.,3.4,6.5,1.6,0.,2.7,4.8,7.9,0.,
$ 1.0,3.1,2.2,0./), SHAPE=(/LDR1,LDR2,N3/))
WRITE(*,*) 'X ='
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (X(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
* Initialize trig table and get factors of N1, N2 and N3
CALL SFFTC3(0,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
$ IFAC,SW,0,IERR)
* Compute 3-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform because LDX1 < 2*(N1/2+1)
CALL SFFTC3(-1,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place forward FFT of X:'
WRITE(*,*)'Y ='
DO K = 1, N3
DO I = 1, N1/2+1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J,K)),
$ ',',AIMAG(Y(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
* Compute 3-dimensional in-place forward FFT.
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
CALL SFFTC3(-1,N1,N2,N3,ONE,V,LDR1,LDR2,V,LDR1/2,LDR2,TRIGS,
$ IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place forward FFT of X:'
CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, N3, V, LDR1/2, LDR2)
* Compute 3-dimensional out-of-place inverse FFT.
* First leading dimension of Z (LDR1) must be even
CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Z,LDR1,LDR2,TRIGS,
$ IFAC,SW,0,IERR)
WRITE(*,*) 'out-of-place inverse FFT of Y:'
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (Z(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
* Compute 3-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Y,2*LDY1,LDY2,
$ TRIGS,IFAC,SW,LW,IERR)
WRITE(*,*) 'in-place inverse FFT of Y:'
CALL PRINT_COMPLEX_AS_REAL(N1, N2, N3, Y, 2*LDY1, LDY2)
DEALLOCATE(SW)
END PROGRAM TESTSC3
SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
REAL A(LD1, LD2, *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
END DO
WRITE(*,*)
END DO
END
SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
INTEGER N1, N2, N3, I, J, K
COMPLEX A(LD1, LD2), *)
DO K = 1, N3
DO I = 1, N1
WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
$ ',',AIMAG(A(I,J,K)),')', J = 1, N2)
END DO
WRITE(*,*)
END DO
END
my_system% f95 -dalign testsc3.f -xlibrary=sunperf
my_system% a.out
Three-dimensional complex-to-real and real-to-complex FFT
X =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
out-of-place forward FFT of X:
Y =
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) ( 6.0, 7.0) ( -7.0, 0.0) ( 6.0, -7.0)
( 3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
in-place forward FFT of X:
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) ( 6.0, 7.0) ( -7.0, 0.0) ( 6.0, -7.0)
( 3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
注释
执行场内实数到复数或复数到实数变换时必须谨慎,应确保输入数组足够大以容纳结果。例如,如果输入的类型是存储在复数数组中的复数且第一个主维是 N,要使用相同的数组存储实数结果,则作为实数输出数组,其第一个主维将是 2 × N。相反,如果输入的类型是存储在实数数组中的实数且第一个主维是 2 × N,要使用相同的数组存储复数结果,则作为复数输出数组,其第一个主维将是 N。可在表 12、表 13 和表 14中找到场内和场外变换的维要求。
在线性和多维 FFT 中,通过实数到复数或复数到实数变换在实数与复数数据之间进行的变换可能会让人困惑,因为 N1 个实数数据点对应于
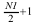 个复数数据点。N1 个实数数据点映射到 N1 个复数数据点,但由于复数数据中有共轭对称性,因此只有
个复数数据点。N1 个实数数据点映射到 N1 个复数数据点,但由于复数数据中有共轭对称性,因此只有
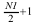 个数据点需要作为复数到实数变换中的输入进行存储,以及作为实数到复数变换中的输出进行存储。在多维 FFT 中,对称性存在于所有维中,而不仅仅在第一个维中。然而,二维和三维 FFT 例程将存储第二个和第三个维的全部复数数据。
个数据点需要作为复数到实数变换中的输入进行存储,以及作为实数到复数变换中的输出进行存储。在多维 FFT 中,对称性存在于所有维中,而不仅仅在第一个维中。然而,二维和三维 FFT 例程将存储第二个和第三个维的全部复数数据。
虽然 FFT 例程接受任意大小的 N1、N2 和 N3,但如果将 N1、N2 和 N3 的值分解为相对较小的质数,则可以最有效地计算 FFT。如果满足以下条件,则可以最有效地计算实数到复数或复数到实数变换
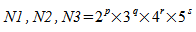 ,
,
在以下情况下,可以最有效地计算复数到复数变换:
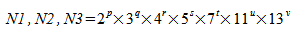 ,
,
其中 p、q、r、s、t、u 和 v 是整数,且 p、q、r、s、t、u、v ≥ 0。
可使用函数 xFFTOPT 确定最佳序列长度,如示例 14 所示。给定输入序列长度后,该函数将返回大小最接近原始长度的最佳长度。
示例 14 RFFTOPT 示例my_system% cat fft_ex01.f
PROGRAM TEST
INTEGER N, N1, N2, N3, RFFTOPT
C
N = 1024
N1 = 1019
N2 = 71
N3 = 49
C
PRINT *, 'N Original N Suggested'
PRINT '(I5, I12)', (N, RFFTOPT(N))
PRINT '(I5, I12', (N1, RFFTOPT(N1))
PRINT '(I5, I12)', (N2, RFFTOPT(N2))
PRINT '(I5, I12)', (N3, RFFTOPT(N3))
END
my_system% f95 -dalign fft_ex01.f -library=sunperf
my_system% a.out
N Original N Suggested
1024 1024
1019 1024
71 72
49 49
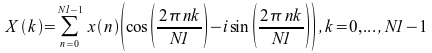 。
。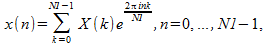
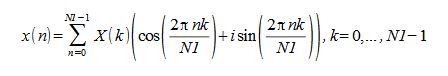
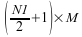 ,
,