2.3.4 渐进下溢的误差属性

在大多数情况下，浮点结果都是舍入的：

computed result = true result + round-off

用来表示误差大小的一种简便尺度称为最后位置单元，简称 ulp。用标准表示法表示的浮点数小数的最低有效位即是其最后一位。用这一位表示的值（例如，除了这一位外，表示法完全相同的两个数字绝对差值）是该数字的最后位置单元。如果计算结果是通过将真正结果舍入到最接近的可表示数字得到的，则显然，舍入误差不会大于计算结果最后位置单元的一半。换而言之，在采用就近舍入模式的 IEEE 算法中，其计算结果如下所示：

0 ≤ |舍入| ≤½ulp

请注意，ulp 是相对值。如果数字非常大，其 ulp 本身就非常大，而如果数字非常小，其 ulp 本身也非常小。将 ulp 表示为函数，这种关系会更明显：ulp(x) 表示浮点数 x 最后位置单元。

另外，浮点数的 ulp 还取决于该数字的表示精度。例如，Table 2–12 显示了上述四个浮点格式的 ulp(1) 值：

表 2-12  四种不同精度的 ulp(1)

精度 值 单精度 ulp(1) = 2^-23 ~ 1.192093e-07 双精度 ulp(1) = 2^-52 ~ 2.220446e-16 双精度扩展 (x86) ulp(1) = 2^-63 ~ 1.084202e-19 四倍精度 ulp(1) = 2^-112 ~ 1.925930e-34

请记住，只有有限数字集才能用计算机算法准确表示。随着数字的数量级的降低并接近零，相邻可表示数字之间的差距会变小。相反，当数字的数量级增加时，相邻可表示数字之间的差距将变大。

例如，假定您要使用只有三个精度位的二进制算法。那么，在任意两个 2 的幂之间，有 2³ = 8 个可表示数字，如下图所示。

图 2-6  数轴

数轴显示了数字之间的差距是随着指数增加而加倍增加的。

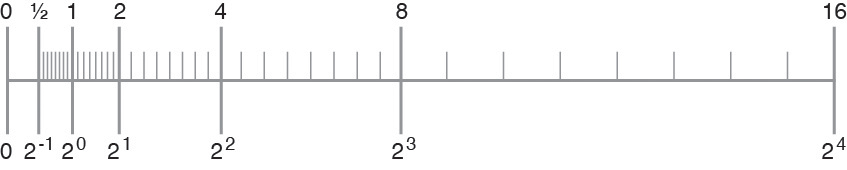
在 IEEE 单精度格式中，两个最小正次正规数之间的差大约是 10^{- 45}，而两个最大有限数之间的数量级差大约是 10³¹！

在Table 2–13 中，nextafter(x,+∞) 表示在沿着数轴向 +∞ 移动的过程中，x 之后的下一个可表示数字。

表 2-13  可表示的单精度格式浮点数之间的差距

x nextafter(x, +·) 差距 0.0 1.4012985e–45 1.4012985e–45 1.1754944e–38 1.1754945e–38 1.4012985e–45 1.0 1.0000001 1.1920929e–07 2.0 2.0000002 2.3841858e–07 16.000000 16.000002 1.9073486e–06 128.00000 128.00002 1.5258789e–05 1.0000000e+20 1.0000001e+20 8.7960930e+12 9.9999997e+37 1.0000001e+38 1.0141205e+31

所有传统的可表示浮点数集都有一个属性，不准确结果的最差情况是：引入一个不大于计算结果中可表示相邻数字之间的距离的误差。将次正规数加到可表示集上并实施渐进下溢时，不准确结果或下溢结果的最差情况是：引入一个不大于计算结果中可表示相邻数字之间的距离的误差。

尤其是，在零与最小正规数之间的区域，任意两个相邻数字之间的距离等于零与最小次正规数之间的距离。 利用次正规数，可以避免出现以下情况：引入的舍入误差大于最近可表示数字之间的距离。

由于没有计算引起的舍入误差会大于与计算结果任意可表示相邻数字的距离，所以许多强大的算法环境都符合以下三条属性：

• x ≠ y 当且仅当 x – y ≠ 0

• (x – y) + y ≈ x，在 x 和 y 二者中较大者的舍入误差内

• 1/(1/x) ≈ x，当 x 是正规化数时，表示 1/x ≠ 0，甚至对于最大正规化 x 也是如此

另一种下溢方案是突然下溢，它是将下溢结果刷新为零。 只要 x – y 出现下溢，突然下溢就会违反第一条和第二条属性。另外，当 1/x 出现下溢时，突然下溢还将违反第三条属性。

我们用 λ 表示最小正正规化数，也称为下溢阈值。 这样，就可以用 λ 来比较渐进下溢和突然下溢的误差属性。

渐进下溢：|误差| < ½λ 的 ulp

突然下溢：|误差| ≈ λ

用 λ 最后位置单元的一半与 λ 本身存在着显著的差别。