4.5 処理速度の向上

コンパイラがプログラムの大量の時間が消費される部分を並列化しない場合、速度の向上は発生しません。たとえば、プログラム実行の 5% 部分に相当するループしか並列化できない場合、全体的に速度を向上できる限界は 5% です。ただし、改善は、負荷のサイズと並列実行オーバーヘッドに依存します。

したがって、一般的な規則として、プログラムの並列化される部分が大きくなればなるほど、大幅な速度の向上を期待できます。

それぞれの並列ループは、起動時と終了時に小さなオーバーヘッドを招きます。起動時のオーバーヘッドには作業を分散するためのものがあり、終了時には、バリアでの同期によるものがあります。ループによって実行される作業量が比較的小さい場合には、速度の向上を期待できません。実際には、ループが遅くなる可能性さえあります。プログラム実行の大部分が大量の小さな並列ループで占められている場合には、プログラム全体の速度が上がる代わりに遅くなることがあります。

コンパイラは、いくつかのループ変換を実行することで、ループの規模を大きくしようとします。この変換には、ループの交換およびループの融合が含まれます。プログラム内の並列化が少ない場合や小さな並列領域に分割されている場合、速度の向上は通常は少なくなります。

問題サイズを大きくすると、多くの場合、プログラム内の並列化の分割が改善されます。たとえば、あるプログラムが順次実行する部分がプログラムサイズの 2 乗に増加し、並列化可能な部分が 3 乗に増加するものとします。この問題の場合、並列化部分の作業負荷は順次部分より速い速度で増加します。リソースの限界に達しないかぎり、ある時点で問題の速度が向上します。

並列 C の利点を最大限に引き出すには、指令、問題のサイズ、およびプログラムの再構成に関して何らかのチューニングや実験を試みてください。

4.5.1 アムダールの法則

決まったサイズの問題の処理速度の向上は一般に、特定の問題の並列処理速度の向上は、問題の逐次処理部分によって制限されるというアムダールの法則に基づきます。次の等式は、問題の処理速度向上を S とし、その問題で順次コードにかかった時間を F とし、それ以外の時間 (1-F) をプロセッサの数である P で均一に除算します。式 ((1 - F) / P) の 2 番目の項の値がゼロになると、値が決まっている 1 番目の項によって全体的な速度の向上度が制限されます。

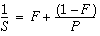
次の図に、この概念を示します。暗い陰影の付いた部分は、プログラムの順次部分を表しており、プロセッサ数が 1、2、4、8 個の場合でも一定のままです。明るい陰影の付いた部分はプログラムの並列部分を表しており、任意の数のプロセッサ間で均等に分散できます。

図 2  固定の問題の速度向上

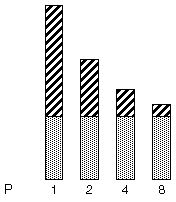
プロセッサの数が増加するにつれ、各プログラムの並列処理部分の所要時間は減少していますが、各プログラムの逐次処理部分は同じままです。

ただし実際には、複数のプロセッサに対する通信と作業分散によりオーバーヘッドを招く場合があります。これらのオーバーヘッドは、使用される任意の数のプロセッサのために固定されない可能性があります。

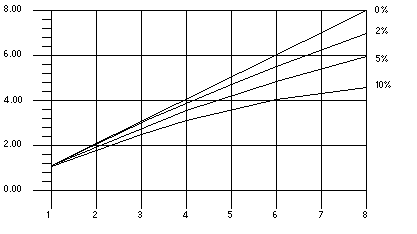
次の図には、プログラムに逐次処理部分がそれぞれ 0%、2%、5%、10% 含まれる場合の理想的な速度向上が示されています。オーバーヘッドは想定されていません。

図 3  アムダールの法則による処理速度向上の曲線

4.5.1.1 オーバーヘッド

モデルにオーバーヘッドの影響を取り入れると、速度向上の曲線は大幅に変わります。説明の目的のために、オーバーヘッドが 2 つの部分で構成されることを想定します: プロセッサの数に依存しない固定部分と、使用されるプロセッサの数に 2 乗で増加する固定でない部分です。

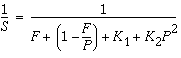
この式で K₁ と K₂ は一定の係数です。この仮定では、速度向上の曲線は次の図のようになります。この場合、速度向上はピークアウトします。特定のポイント後は、より多くのプロセッサを追加するとはパフォーマンスに悪影響を与えます。

図 4  オーバーヘッドがある場合の速度向上の曲線

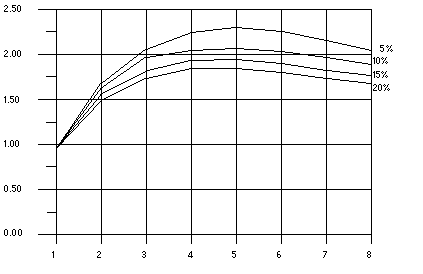
グラフは、すべてのプログラムが 5 つのプロセッサで最大の速度向上に達し、最大の 8 個のプロセッサが追加されるとこの利点が失われることを示しています。横軸はプロセッサの数、縦軸は速度を表しています。

4.5.1.2 ガスタフソンの法則

アムダールの法則は、実際の問題で並列化速度向上を予測する場合に、誤った方向に導かれる可能性があります。プログラムの逐次処理部分に費やされる時間の割合は、問題のサイズに依存することがあります。つまり、次の例に示すように、問題のサイズを大きくすることで、速度向上の可能性が改善する場合があります。

使用例 22  問題サイズの拡大により速度向上の可能性が改善されることがある

/*
* initialize the arrays
*/
for (i=0; i < n; i++) {
    for (j=0; j < n; j++) {
            a[i][j] = 0.0;
            b[i][j] = ...
            c[i][j] = ...
    }
}
/*
* matrix multiply
*/
for (i=0; i < n; i++) {
    for(j=0; j < n; j++) {
            for (k=0; k < n; k++) {
                a[i][j] = b[i][k]*c[k][j];
            }
    }
}

理想的なオーバーヘッドゼロ、2 番目のループネストが並列で実行されることを想定します。問題のサイズが小さい場合 (つまり、小さい値の n)、プログラムの順次部分と並列化部分はそれほどかけ離れていません。ただし、n が大きくなると、並列実行部分に費やされる時間が順次実行の部分に対するものよりも早い勢いで大きくなります。この問題の場合は、問題のサイズが大きくなるにつれてプロセッサの数を増やすことは利点です。