2.2.6 10 進数表現の範囲と精度
このセクションでは、特定の格納形式での範囲と精度の概念について説明します。ここでは、IEEE の単精度、倍精度、4 倍精度の各形式、および x86 アーキテクチャー上での IEEE 拡張倍精度形式の実装に対応する範囲と精度について説明します。範囲と精度の概念を定義する場合の具体的な例については、IEEE 単精度形式を参照してください。
IEEE 規格では、単精度形式の浮動小数点数を表すために 32 ビットを使用することが規定されています。32 個の 0 と 1 の組み合わせは有限数しか存在しないため、32 ビットでは有限数の数値しか表すことができません。
この特定の形式で表すことができる最大と最小の正の数値の 10 進数表現は何かと尋ねるのは自然なことです。
範囲の概念を導入すると、その質問を言い換えて、代わりに IEEE 単精度形式で表すことができる数値の範囲 (10 進数表記) は何かと尋ねることができます。
IEEE 単精度形式の正確な定義を考慮に入れ、正の正規化数に限定すると、IEEE 単精度形式で表すことができる浮動小数点数の範囲は次のようになると証明できます。
1.175...× (10-38) から 3.402... ×(10+38) まで
2 番目の質問は、特定の形式で表される数値の精度に関するものです。 これらの概念は、いくつかの状況と例を調べることによって説明できます。
2 進浮動小数点演算のための IEEE 規格では、単精度形式で表すことができる数値のセットが規定されています。この数値のセットは、2 進浮動小数点数のセットとして説明されます。IEEE 単精度形式の仮数は 23 ビットあり、これが暗黙的先行ビットとともに 24 桁 (ビット) の (2 進数の) 精度を生み出します。
次の数値 (10 進数の仮数 q 桁で表現できます) を 数直線 上にマークすることによって、異なる数値のセットが取得されます。
x = (x1.x2 x3...xq) × (10n)
次の図は、この状況を示しています。
図 2-5 デジタル表現と 2 進数表現で定義される数値のセットの比較
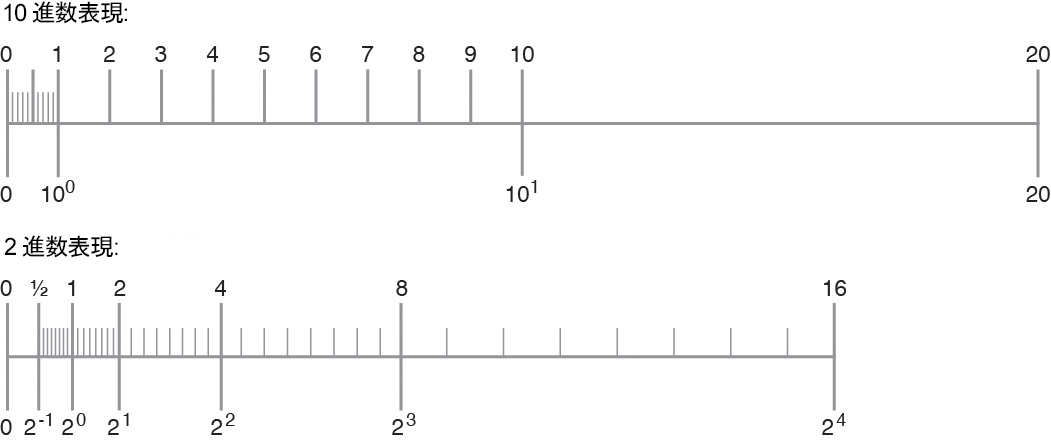
この 2 つのセットは異なることに注意してください。そのため、2 進数の有効桁数 24 桁に対応する 10 進数の有効桁数を推定するには、問題を再公式化する必要があります。
2 進数表現 (コンピュータによって使用される内部形式) と 10 進数形式 (ユーザーが通常関心を持つ形式) の間で浮動小数点数を変換するという観点から問題を再公式化します。実際に、10 進数から 2 進数に変換したあと 10 進数に戻したり、2 進数から 10 進数に変換したあと 2 進数に戻したりすることがあります。
数値のセットが異なるため、変換は一般に不正確である点に注意することが重要です。正しく実行された場合、あるセット内の数値からもう一方のセット内の数値への変換では、2 番目のセットから 2 つの隣接する数値のうちの 1 つが選択されます (具体的にどちらを選択するかは丸めに関連した問題です)。
いくつかの例を考察します。IEEE 単精度形式の次の 10 進数表現で数値を表そうとしているとします。
x = x1.x2 x3... × 10n
IEEE 単精度形式で正確に表すことができる実数は有限数しか存在せず、またその中に上の形式のすべての数値が含まれているわけではないため、一般に、このような数値を正確に表すことは不可能です。たとえば、
y = 838861.2, z = 1.3
として、次の Fortran プログラムを実行します。
REAL Y, Z
Y = 838861.2
Z = 1.3
WRITE(*,40) Y
40 FORMAT("y: ",1PE18.11)
WRITE(*,50) Z
50 FORMAT("z: ",1PE18.11)
このプログラムからの出力は、次のようになるはずです。
y: 8.38861187500E+05 z: 1.29999995232E+00
y に割り当てられた値 8.388612 × 105 と出力された値の差は 0.000000125 です。これは、y より 10 進数の 7 桁小さい値です。y を IEEE 単精度形式で表したときの正確性は、有効桁数が約 6 から 7 です。あるいは、y は、IEEE 単精度形式で表された場合、有効桁数が約 6 です。
同様に、z に割り当てられた値 1.3 と出力された値の差は 0.00000004768 です。これは、z より 10 進数の 8 桁小さい値です。z を IEEE 単精度形式で表したときの正確性は、有効桁数が約 7 から 8 です。あるいは、z は、IEEE 単精度形式で表された場合、有効桁数が約 7 です。
10 進数の浮動小数点数 a を IEEE 単精度形式の 2 進数表現 b に変換したあと、b を 10 進数 c に戻すとします。a と a - c の間には何桁あるでしょうか。
この質問を次のように言い換えます。
IEEE 単精度形式表現の a の 10 進数の有効桁数は何桁でしょうか。あるいは、x を IEEE 単精度形式で表したとき、正確であるとして信頼できる 10 進数の桁数は何桁でしょうか。
10 進数の有効桁数は常に 6 から 9 まで (つまり、少なくとも 6 桁) であり、9 桁を超えて正確であることはありません (変換が正確である場合、つまり無限数の桁を正確にできる場合を除く)。
逆に、IEEE 単精度形式の 2 進数を 10 進数に変換したあと 2 進数に戻す場合は、一般に、これらの 2 つの変換のあとに最初の数値を確実に取得できるようにするために少なくとも 10 進数 9 桁を使用する必要があります。
全体のまとめをTable 2–10 に示します。
|