スパース行列
スパース行列は、通常、必要な格納領域を最小限に抑える形式で表されます。疎であることの利点を活かし、ゼロを格納しないことによって、かなりの格納領域を節約できます。SPSOLVE および SuperLU で使用される格納形式は圧縮スパース列 (CSC) 形式で、これは Harwell-Boeing 形式とも呼ばれます。
CSC 形式では、スパース行列を 2 つの整数配列と 1 つの浮動小数点配列で表します。整数配列 (colptr と rowind) はスパース行列の非ゼロの位置を指定し、浮動小数点配列 (values) は非ゼロ値に使用されます。
列ポインタ (colptr) 配列は n+1 個の要素で構成されています。colptr(i) は i 番目の列の先頭を指し、colptr(i+1)-1 は i 番目の列の末尾を指します。行インデックス (rowind) 配列には非ゼロ値の行インデックスが格納されます。values 配列には、対応する非ゼロの数値が格納されます。
neqns 個の方程式と nnz 個の非ゼロ要素から成るスパース行列には次の行列データ形式が存在します。
対称
構造的対称
非対称
現在、SuperLU は非対称行列のみをサポートしています。多くの場合、もっとも効率的なデータ表現は具体的な問題によって異なります。以降のセクションでは、スパース行列データ形式の例を示します。
対称スパース行列
対称スパース行列は、すべての i および j について a(i, j) = a(j, i) である行列です。この対称性のため、ソルバールーチンに渡す必要があるのは下側の三角形の値のみです。上側の三角形は下側の三角形から判断できます。
対称行列の例を次に示します。この例の出典は、A. George および J. W-H. Liu 著、『Computer Solution of Large Sparse Positive Definite Systems』です。

A を CSC 形式で表すには、次のようにします。
colptr: 1, 6, 7, 8, 9, 10
rowind: 1, 2, 3, 4, 5, 2, 3, 4, 5
values: 4.0, 1.0, 2.0, 0.5, 2.0, 0.5, 3.0, 0.625, 16.0
構造的対称スパース行列
構造的対称スパース行列では、その非ゼロ値が、すべての i および j について、a(i, j) ≠ 0 であれば a(j, i) ≠ 0 であるという性質を持ちます。構造的対称行列の連立方程式を解く場合は、行列全体をソルバールーチンに渡す必要があります。
構造的対称行列の例を次に示します。
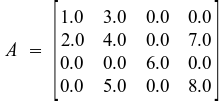
A を CSC 形式で表すには、次のようにします。
colptr: 1, 3, 6, 7, 9
rowind: 1, 2, 1, 2, 4, 3, 2, 4
values: 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0
非対称スパース行列
非対称スパース行列では、すべての i および j について a(i, j) = a(j, i) となるわけではありません。行列の構造には明白なパターンがありません。非対称行列の連立方程式を解く場合は、行列全体をソルバールーチンに渡す必要があります。非対称行列の例を次に示します。

A を CSC 形式で表すには、次のようにします。
1 オリジンのインデックス:
colptr: 1, 6, 7, 8, 9, 11
rowind: 1, 2, 3, 4, 5, 2, 3, 4, 2, 5
values: 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0
0 オリジンのインデックス:
colptr: 0, 5, 6, 7, 8, 10
rowind: 0, 1, 2, 3, 4, 1, 2, 3, 1, 4
values: 1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0, 10.0