順方向および逆方向 FFT ルーチン

言語:

次の表に、 FFT ルーチンの名前とそれらの呼び出しシーケンスを一覧表示します。倍精度ルーチン名は角括弧で囲んでいます。引数のデータ型とサイズの詳細については、個々のマニュアルページを参照してください。

表 9 FFT 1 次元ルーチンとそれらの引数

ルーチン名	引数
`CFFTS` `[ZFFTD]`	`(OPT,` `N1,` `SCALE,` `X,` `Y,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`SFFTC` `[DFFTZ]`	`(OPT,` `N1,` `SCALE,` `X,` `Y,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`CFFTSM` `[ZFFTDM]`	`(OPT,` `N1,` `N2,` `SCALE,` `X,` `LDX1,` `Y,` `LDY1,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`SFFTCM` `[DFFTZM]`	`(OPT,` `N1,` `N2,` `SCALE,` `X,` `LDX1,` `Y,` `LDY1,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`CFFTC` `[ZFFTZ]`	`(OPT,` `N1,` `SCALE,` `X,` `Y,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`CFFTCM` `[ZFFTZM]`	`(OPT,` `N1,` `N2,` `SCALE,` `X,` `LDX1,` `Y,` `LDY1,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`

表 10 FFT 2 次元ルーチンとそれらの引数

ルーチン名	引数
`CFFTS2` `[ZFFTD2]`	`(OPT,` `N1,` `N2,` `SCALE,` `X,` `LDX1,` `Y,` `LDY1,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`SFFTC2` `[DFFTZ2]`	`(OPT,` `N1,` `N2,` `SCALE,` `X,` `LDX1,` `Y,` `LDY1,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`CFFTC2` `[ZFFTZ2]`	`(OPT,` `N1,` `N2,` `SCALE,` `X,` `LDX1,` `Y,` `LDY1,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`

表 11 FFT 3 次元ルーチンとそれらの引数

ルーチン名	引数
`CFFTS3` `[ZFFTD3]`	`(OPT,` `N1,` `N2,` `N3,` `SCALE,` `X,` `LDX1,` `LDX2,` `Y,` `LDY1,` `LDY2,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`SFFTC3` `[DFFTZ3]`	`(OPT,` `N1,` `N2,` `N3,` `SCALE,` `X,` `LDX1,` `LDX2,` `Y,` `LDY1,` `LDY2,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`
`CFFTC3` `[ZFFTZ3]`	`(OPT,` `N1,` `N2,` `N3,` `SCALE,` `X,` `LDX1,` `LDX2,` `Y,` `LDY1,` `LDY2,` `TRIGS,` `IFAC,` `WORK,` `LWORK,` `ERR)`

Oracle Developer Studio パフォーマンスライブラリ FFT ルーチンは次の引数を使用します。

OPT: ルーチンを初期化のために呼び出すか、または変換を計算するために呼び出すかを示すフラグ。
N1、N2、N3: 1、2、3 次元変換の問題の次元。
X: 入力配列。ここで、X の型は、ルーチンが複素数-複素数変換または複素数-実数変換の場合は COMPLEX です。実数-複素数変換の場合の X の型は REAL です。
Y: 出力配列。ここで、Y の型は、ルーチンが複素数-複素数変換または実数-複素数変換の場合は COMPLEX です。複素数-実数変換の場合の Y の型は REAL です。
LDX1、LDX2 および LDY1、LDY2: LDX1 および LDX2 は入力配列のリーディングディメンジョンで、LDY1 と LDY2 は出力配列のリーディングディメンジョンです。FFT ルーチンでは、出力で入力を上書きする (インプレース変換) ことも、出力を入力配列と別の配列に格納する (アウトオブプレース変換) こともできます。複素数-複素数変換では、入力データは出力データと同じサイズです。ただし、実数-複素数および複素数-実数変換では、入力データと出力データのメモリー要件が異なります。インプレース変換を計算する場合は、入力配列に、変換結果を収容するための十分な大きさがあることを注意して確認する必要があります。
TRIGS: 三角法の重みを格納する配列。
IFAC: 問題の次元の係数を格納する配列。問題のサイズは次のとおりです。
- 1 次元 FFT: 次元 N1 の問題のサイズ
- 2 次元 FFT: 次元 N1 および N2 の問題のサイズ
- 3 次元 FFT: 次元 N1、N2、N3 の問題のサイズ
N1、N2、および N3 は任意のサイズにできますが、実数-複素数または複素数-実数の変換は、次の場合にもっとも効率的に計算できます。

、

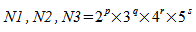また、複素数-複素数変換は次の場合にもっとも効率的に計算されます:

、

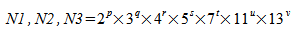ここで、p、q、r、s、t、u、および v は整数で、p、q、r、s、t、u、v ≥ 0 です。
WORK: ワークスペース。このサイズはルーチンと、ルーチンが並列化されている場合に、変換を計算するために使用されているスレッドの数によって異なります。
LWORK: ワークスペースのサイズ。LWORK がゼロの場合、ルーチンは必要なサイズでワークスペースを割り当てます。
SCALE: 出力をスケーリングするスカラー。文献では、逆変換が 1 次元変換の場合に 1/N1、2 次元変換の場合に 1/(N1 × N2)、および 3 次元変換の場合に 1/(N1 × N2 × N3) のスケーリング係数で定義されていることがあります。そのような場合、逆変換は正規化されていると言います。正規化 FFT のあとにその逆方向 FFT が行われると、結果は元の入力データになります。Oracle Developer Studio パフォーマンスライブラリ FFT ルーチンは正規化されません。ただし、SCALE に格納されている適切なスケーリング係数で逆方向 FFT ルーチンを呼び出すことによって、正規化を簡単に実行できます。
ERR: ルーチンでエラーが検出された場合はゼロ以外の値を返し、それ以外の場合はゼロを返すフラグ。

1 次元 FFT ルーチン

1 次元 FFT ルーチンは、1 次元のみの実数または複素数データの FFT を計算します。データは 1 つ以上の複素数または実数のシーケンスです。1 つのシーケンスの場合、データはベクトルに格納されます。複数のシーケンスが変換される場合は、2 次元配列で列方向にシーケンスが格納され、1 次元 FFT が列方向に沿ってシーケンスごとに計算されます。 1 次元順方向 FFT ルーチンは次を計算します。 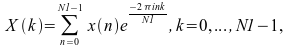$image:X(k) = {n = 0} から {N1 - 1} までの x(n)e^{{-2πink} / N1} の合計, k = 0, ..., N1 - 1,$ ここで image:i = -1 の平方根。

または極形式で表すと: image:X(k) = {n = 0} から {N1 - 1} までの x(n) (cos ({2πnk} / N1) - i sin ({2πnk} / N1)) の合計, k = 0, ...,N1 - 1 。

逆方向 FFT ルーチンは、次を計算します $image:x(n) = {k = 0} から {N1 - 1} までの X(k)e^{{2πink} / N1} の合計, n = 0, ..., N1 - 1,$

極形式では: image:x(n) = {n = 0} から {N1 - 1} までの X(k) (cos ({2πnk} / N1) + i sin ({2πnk} / N1)) の合計, k = 0, ...,N1 - 1

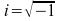順変換では、入力がサイズ N1 の 1 つ以上の複素数シーケンスである場合、結果は、それぞれ N 1 の無関係なデータポイントから構成される 1 つ以上の複素数シーケンスになります。ただし、入力が、それぞれ N1 の実数データポイントを含む 1 つ以上の実数シーケンスである場合、結果は、共役対称な 1 つ以上の複素数シーケンスになります。つまり:

image:x(n) = {n = 0} から {N1 - 1} までの X(k) (cos ({2πnk} / N1) - i sin ({2πnk} / N1)) の合計, k = 0, ...,N1 - 1

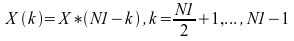
X(0) の虚部は常に 0 です。N1 が偶数の場合、 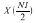image:X ({N1 / 2}) の虚部もゼロです。両方のゼロは明示的に格納されます。各シーケンスの後半は前半から得られるため、 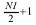image:(N1 / 2) + 1 複素数データポイントのみが計算され、出力配列に格納されます。この章のここやほかの場所で、整数除算は切り捨てています。

逆変換では、N1 ポイントの複素数-複素数変換が計算される場合、各入力シーケンスに N1 の無関係なデータポイントが期待され、出力配列で N1 データポイントが返されます。ただし、N1 ポイントの複素数-実数変換が計算される場合、入力に、各共役対称入力シーケンスの最初の 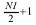image:(N1 / 2) + 1 の複素数データポイントのみが期待され、ルーチンは各出力シーケンスで N1 の実数データポイントを返します。

N1 の値ごとに、順変換または逆変換ルーチンを呼び出して、実際の FFT を計算する前に、N1 の係数と、それらの係数に関連付けられる三角法の重みを計算する必要があります。係数と三角法の重みは、N1 が変更されないかぎり、その後の変換で再利用できます。

次の表の表 12 に、単精度 1 次元 FFT ルーチンとその目的を示します。入力および出力として 2 次元配列を使用するルーチンについては、表 12 に、リーディングディメンジョン要件も示しています。同じ情報は、データ型が倍精度と倍精度複素数であることを除いて、対応する倍精度ルーチンに適用します。マッピングについては、表 12 を参照してください。ルーチンとその引数の詳細な説明については、個々のマニュアルページを参照してください。

表 12 単精度 1 次元 FFT ルーチン

名前	目的	入力のサイズおよび型	出力のサイズおよび型	リーディングディメンジョン要件
`SFFTC`	`OPT` = 0 初期化
	`OPT` = -1 単一ベクトルの実数-複素数の順方向 1 次元 FFT	`N`1、実数	, 複素数
`SFFTC`	`OPT` = 0 初期化
	`OPT` = 1 単一ベクトルの複素数-実数の逆方向 1 次元 FFT	, 複素数	`N`1 実数
`CFFTC`	`OPT` = 0 初期化
	`OPT` = -1 単一ベクトルの複素数-複素数の順方向 1 次元 FFT	`N`1、複素数	`N`1、複素数
	`OPT` = 1 単一ベクトルの複素数-複素数の逆方向 1 次元 FFT	`N`1、複素数	`N`1、複素数
`SFFTCM`	`OPT` = 0 初期化
	`OPT` = -1 M ベクトルの実数-複素数の順方向 1 次元 FFT	`N`1 × `M`、実数	、複素数	`LDX1` = 2 × `LDY1`	`LDX1` ≥ `N`1
`CFFTSM`	`OPT` = 0 初期化
	`OPT` = 1 M ベクトルの複素数-実数の逆方向 1 次元 FFT	、複素数	`N`1 × `M`、実数	`LDX1` ≥ `LDY1`=2 × `LDX1`	`LDX1` ≥ `LDY1` ≥ `N`1
`CFFTCM`	`OPT` = 0 初期化
	`OPT` = -1 M ベクトルの複素数-複素数の順方向 1 次元 FFT	`N`1 × `M`、複素数	`N`1 × `M`、複素数	`LDX1` ≥ `N`1 `LDY1` ≥ `N`1	`LDX1` ≥ `N`1 `LDY1` ≥ `N`1
	`OPT` = 1 M ベクトルの複素数-複素数の逆方向 1 次元 FFT	`N`1 × `M`、複素数	`N`1 × `M`、複素数	`LDX1` ≥ `N`1 `LDY1` ≥ `N`1	`LDX1` ≥ `N`1 `LDY1` ≥ `N`1

注 - 表 12 に関して、次のことに注意してください。

LDX1 は入力配列のリーディングディメンジョンです。
LDY1 は出力配列のリーディングディメンジョンです。
N1 は FFT 問題の最初の次元です。
N2 は FFT 問題の 2 番目の次元です。
OPT = 0 でルーチンを呼び出して、ルーチンを初期化する場合に、実行される唯一のエラーチェックは、N1 < 0 かどうかを判断することです

次の例は、一連のシーケンスの 1 次元実数-複素数および複素数-実数 FFT の計算方法を示しています。

使用例 10 1 次元実数-複素数 FFT および複素数-実数 FFT

my_system% cat testscm.f
       PROGRAM TESTSCM
       IMPLICIT NONE
       INTEGER :: LW, IERR, I, J, K, LDX, LDC
       INTEGER,PARAMETER :: N1 = 3, N2 = 2, LDZ = N1, 
      $        LDC = N1, LDX = 2*LDC
       INTEGER, DIMENSION(:) :: IFAC(128)
       REAL :: SCALE
       REAL, PARAMETER :: ONE = 1.0
       REAL, DIMENSION(:) :: SW(N1), TRIGS(2*N1)
       REAL, DIMENSION(0:LDX-1,0:N2-1) :: X, V, Y
       COMPLEX, DIMENSION(0:LDZ-1, 0:N2-1) :: Z
* workspace size	
       LW = N1
       SCALE = ONE/N1
       WRITE(*,*)	
      $ 'Linear complex-to-real and real-to-complex FFT of a sequence'
       WRITE(*,*)
       X = RESHAPE(SOURCE = (/.1, .2, .3,0.0,0.0,0.0,7.,8.,9.,
      $    0.0, 0.0, 0.0/), SHAPE=(/6,2/))	 
       V = X
       WRITE(*,*) 'X = '
       DO I = 0,N1-1
         WRITE(*,'(2(F4.1,2x))') (X(I,J), J = 0, N2-1)
       END DO
       WRITE(*,*)
* intialize trig table and compute factors of N1
       CALL SFFTCM(0, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC, 
      $ SW, LW, IERR)
       IF (IERR .NE. 0) THEN 
          PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
          STOP
       END IF
 
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
       CALL SFFTCM(-1, N1, N2, ONE, X, LDX, Z, LDZ, TRIGS, IFAC,
      $            SW, 0, IERR)
      IF (IERR .NE. 0) THEN
        PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
        STOP 
      END IF
      WRITE(*,*) 'out-of-place forward FFT of X:'
      WRITE(*,*)'Z ='
      DO I = 0, N1/2
         WRITE(*,'(2(A1, F4.1,A1,F4.1,A1,2x))') ('(',REAL(Z(I,J)),
     $ ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
      END DO
      WRITE(*,*)
* Compute in-place forward linear FFT.
* X must be large enough to store N1/2+1 complex values
      CALL SFFTCM(-1, N1, N2, ONE, X, LDX, X, LDC, TRIGS, IFAC,
     $            SW, LW, IERR)
      IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP
      END IF
      WRITE(*,*) 'in-place forward FFT of X:'
      CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, X, LDC, N2)
      WRITE(*,*)
* Compute out-of-place inverse linear FFT.
      CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, X, LDX, TRIGS, IFAC,
     $            SW, LW, IERR)
      IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP
      END IF
      WRITE(*,*) 'out-of-place inverse FFT of Z:'
      DO I = 0, N1-1
         WRITE(*,'(2(F4.1,2X))') (X(I,J), J = 0, N2-1)
      END DO
      WRITE(*,*)
* Compute in-place inverse linear FFT.
      CALL CFFTSM(1, N1, N2, SCALE, Z, LDZ, Z, LDZ*2, TRIGS,
     $            IFAC, SW, 0, IERR)
      IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP 
      END IF
 
      WRITE(*,*) 'in-place inverse FFT of Z:'
      CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Z, LDZ*2, N2)
      WRITE(*,*)
      END PROGRAM TESTSCM
      SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2) 
      INTEGER N1, N2, N3, I, J, K
      REAL A(LD1, LD2, *)
      DO K = 1, N3
         DO I = 1, N1
            WRITE(*,'(5(F4.1,2X))') (A(I,J,K), J = 1, N2)
         END DO 
         WRITE(*,*)
      END DO
      END
      SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
      INTEGER N1, N2, N3, I, J, K
      COMPLEX A(LD1, LD2, *)
      DO K = 1, N3
         DO I = 1, N1
            WRITE(*,'(5(A1, F4.1,A1,F4.1,A1,2X))') ('(',REAL(A(I,J,K)),
     $            ',',AIMAG(A(I,J,K)),')', J = 1, N2)
         END DO
         WRITE(*,*)
      END DO
      END
my_system% f95 -dalign testscm.f -xlibrary=sunperf
my_system% a.out
Linear complex-to-real and real-to-complex FFT of a sequence
X =
0.1 7.0
0.2 8.0
0.3 9.0
out-of-place forward FFT of X:
Z =
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
in-place forward FFT of X:
( 0.6, 0.0) (24.0, 0.0)
(-0.2, 0.1) (-1.5, 0.9)
out-of-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0
 
in-place inverse FFT of Z:
0.1 7.0
0.2 8.0
0.3 9.0

例 7-1 注記:

X の順方向 FFT は実際に次のようになります。

( 0.6, 0.0) (24.0, 0.0) Z = (-0.2, 0.1) (-1.5, 0.9) (-0.2, 0.1) (-1.5, 0.9)

対称性のために、Z(2) は Z(1) の複素共益であるため、最初の 2 つのみの 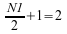image:(N1 / 2) + 1 = 2 複素数値が格納されます。インプレース順変換の場合、実数配列 X を入力および出力として、SFFTCM が呼び出されます。SFFTCM では、出力配列の型を COMPLEX と想定するため、出力配列としての X のリーディングディメンジョンは X が複素数であるかのようにする必要があります。実数配列 X のリーディングディメンジョンは LDX = 2 × LDC であるため、複素数出力配列としての X のリーディングディメンジョンは LDC である必要があります。同様に、インプレース逆変換では、複素数配列 Z を入力および出力として、CFFTSM が呼び出されます。CFFTSM では、出力配列の型を REAL と想定するため、出力配列としての Z のリーディングディメンジョンは Z が実数であるかのようにする必要があります。複素数配列 Z のリーディングディメンジョンは LDZ であるため、実数出力配列としての Z のリーディングディメンジョンは LDZ × 2 である必要があります。

次の例、使用例 11 では、一連のシーケンスの 1 次元複素数-複素数 FFT の計算方法を示しています。

使用例 11 1 次元複素数-複素数 FFT

my_system% cat testccm.f
       PROGRAM TESTCCM
       IMPLICIT NONE
       INTEGER :: LDX1, LDY1, LW, IERR, I, J, K, LDZ1, NCPUS,
      $           USING_THREADS, IFAC(128)
       INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1, LDZ1 = N1,
      $                      LDY1 = N1+2
       REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/N1
       COMPLEX :: Z(0:LDZ1-1,0:N2-1), X(0:LDX1-1,0:N2-1),
      $           Y(0:LDY1-1,0:N2-1)
 
       REAL :: TRIGS(2*N1)
       REAL, DIMENSION(:), ALLOCATABLE :: SW
* get number of threads 
       NCPUS = USING_THREADS()
* workspace size
       LW = 2 * N1 * NCPUS
       WRITE(*,*)'Linear complex-to-complex FFT of one or more sequences'
       WRITE(*,*)
       ALLOCATE(SW(LW))
       X = RESHAPE(SOURCE =(/(.1,.2),(.3,.4),(.5,.6),(.7,.8),(.9,1.0),
      $ (1.1,1.2),(1.3,1.4),(1.5,1.6),(1.7,1.8),(1.9,2.0),(2.1,2.2),
      $ (1.2,2.0)/), SHAPE=(/LDX1,N2/))
       Z = X
       WRITE(*,*) 'X = '
       DO I = 0, N1-1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(X(I,J)),
      $           ',',AIMAG(X(I,J)),')', J = 0, N2-1)
       END DO	
       WRITE(*,*)* intialize trig table and compute factors of N1
       CALL CFFTCM(0, N1, N2, SCALE, X, LDX1, Y, LDY1, TRIGS, IFAC,
      $            SW, LW, IERR)
       IF (IERR .NE. 0) THEN
         PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
         STOP
       END IF
* Compute out-of-place forward linear FFT.
* Let FFT routine allocate memory.
       CALL CFFTCM(-1, N1, N2, ONE, X, LDX1, Y, LDY1, TRIGS, IFAC,
      $            SW, 0, IERR)
       IF (IERR .NE. 0) THEN
          PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
          STOP
       END IF
* Compute in-place forward linear FFT. LDZ1 must equal LDX1
       CALL CFFTCM(-1, N1, N2, ONE, Z, LDX1, Z, LDZ1, TRIGS,
      $            IFAC, SW, 0, IERR)
       WRITE(*,*) 'in-place forward FFT of X:'
       DO I = 0, N1-1 
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Z(I,J)),
      $           ',',AIMAG(Z(I,J)),')', J = 0, N2-1)
       END DO
 
       WRITE(*,*)
       WRITE(*,*) 'out-of-place forward FFT of X:'
       WRITE(*,*) 'Y ='
       DO I = 0, N1-1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
      $        ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
       END DO
       WRITE(*,*)
* Compute in-place inverse linear FFT.
       CALL CFFTCM(1, N1, N2, SCALE, Y, LDY1, Y, LDY1, TRIGS, IFAC,
      $            SW, LW, IERR)
       IF (IERR .NE. 0) THEN
          PRINT*,'ROUTINE RETURN WITH ERROR CODE = ', IERR
          STOP
       END IF
       WRITE(*,*) 'in-place inverse FFT of Y:'
       WRITE(*,*) 'Y ='
       DO I = 0, N1-1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(Y(I,J)),
      $           ',',AIMAG(Y(I,J)),')', J = 0, N2-1)
       END DO
       DEALLOCATE(SW)
       END PROGRAM TESTCCM
my_system% f95 -dalign testccm.f -library=sunperf
my_system% a.out
Linear complex-to-complex FFT of one or more sequences
X =
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)
in-place forward FFT of X:
(  0.9,  1.2) (  2.7,  3.0) (  4.5,  4.8) ( 5.2,  6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1,  0.7)
out-of-place forward FFT of X:
Y = 
(  0.9,  1.2) (  2.7,  3.0) (  4.5,  4.8) ( 5.2,  6.2)
( -0.5, -0.1) ( -0.5, -0.1) ( -0.5, -0.1) ( 0.4, -0.9)
( -0.1, -0.5) ( -0.1, -0.5) ( -0.1, -0.5) ( 0.1,  0.7)
in-place inverse FFT of Y:
Y = 
( 0.1, 0.2) ( 0.7, 0.8) ( 1.3, 1.4) ( 1.9, 2.0)
( 0.3, 0.4) ( 0.9, 1.0) ( 1.5, 1.6) ( 2.1, 2.2)
( 0.5, 0.6) ( 1.1, 1.2) ( 1.7, 1.8) ( 1.2, 2.0)

2 次元 FFT ルーチン

1 次元 FFT ルーチンでは、入力が 2 次元配列の場合、FFT が 1 次元のみに沿って、つまり、配列の列に沿って計算されます。2 次元 FFT ルーチンは、入力として 2 次元配列を受け取り、列と行の両方の次元に沿って FFT を計算します。具体的には、順方向 2 次元 FFT ルーチンは次のように計算します。

$image:X(k,n) = {l = 0} から {N2 - 1} までと {j = 0} から {N1 - 1} までの x(j,l)e^{{-2πiln} / N2} e^{{-2πijk} / N1} の合計, k = 0, ..., N1 - 1, n = 0, ...,N2 - 1$

逆方向 2 次元 FFT ルーチンは次のように計算します。

$image:x(j,l) = {n = 0} から {N2 - 1} までと {k = 0} から {N1 - 1} までの X(k,n)e^{{2πiln} / N2} e^{{2πijk} / N1} の合計, j = 0, ..., N1 - 1, l = 0, ...,N2 - 1$

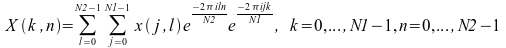
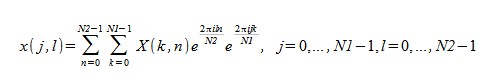
順方向および逆方向の両方の 2 次元変換で、入力問題が N1 × N2 である複素数-複素数変換は、同様に N1 × N2 である複素数配列を生成します。

実数-複素数 2 次元変換 (順方向 FFT) の計算時に、実数入力配列の次元が N1 × N2 である場合、結果は次の次元の複素数配列になります: image:((N1 / 2) + 1) × N2 。

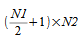逆に、次元 N1 × N2 の複素数-実数変換 (逆方向 FFT) の計算時、 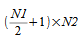image:((N1 / 2) + 1) × N2 複素数配列が入力として必要です。実数-複素数および複素数-実数 1 次元 FFT と同様に、共役対称性のため、最初のみの 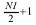image:(N1 / 2) + 1 複素数データポイントが最初の次元に沿って、入力または出力配列に格納される必要があります。複素数部分配列 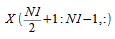image:X ((N1 / 2) + 1 : N1-1,:) は次から取得でき、 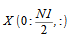image:X (0:{N1 / 2}, :) 次のようになります。

image:X(k,n)=X * (N1 - k,n),{}改行{}k = {N1 / 2} + 1,...,N1 - 1 {}改行{}n = 0,...,N2 - 1

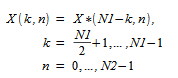
2 次元変換を計算するには、FFT ルーチンを 2 回呼び出す必要があります。1 回の呼び出しでルーチンを初期化し、2 回目の呼び出しで実際に変換を計算します。初期化には、N1 および N2 の係数と、それらの計数に関連付けられる三角法の重みの計算が含まれます。その後の順変換または逆変換では、N1 と N2 が変更されないかぎり、初期化は必要ありません。

重要: 2 次元 FFT ルーチンからの戻り時に、Y(0 : N - 1, :) に変換結果が格納され、Y(N : LDY-1, :) の元の内容が上書きされます。ここで、N = N1 (複素数-複素数および複素数-実数変換の場合)、および N = 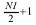image:(N1 / 2) + 1 (実数-複素数変換の場合) です。

次の表の表 13 に、単精度 2 次元 FFT ルーチンとその目的を示します。同じ情報は、データ型が倍精度と倍精度複素数であることを除いて、対応する倍精度ルーチンに適用します。マッピングについては、表 13 を参照してください。ルーチンとその引数の詳細な説明については、個々のマニュアルページを参照してください。

表 13 単精度 2 次元 FFT ルーチン

名前	目的	入力のサイズ、型	出力のサイズ、型	リーディングディメンジョン要件
`SFFTC2`	`OPT` = 0 初期化
	`OPT` = -1 実数-複素数順方向 2 次元 FFT	N1 × N2、実数	、複素数	`LDX1` = 2 × `LDY1` `LDY1` ≥	`LDX1` ≥ `N`1 `LDY1` ≥
`CFFTS2`	`OPT` = 0 初期化
	`OPT` = 1 複素数-実数逆方向 2 次元 FFT	、複素数	`N`1 × `N`2、実数	`LDX1` ≥ `LDY1`=2 × `LDX1`	`LDX1` ≥ `LDY1`≥ 2 × `LDX1` `LDY1` は偶数
`CFFTC2`	`OPT` = 0 初期化
	`OPT` = -1 複素数-複素数順方向 2 次元 FFT	`N`1 × `N`2、複素数	`N`1 × `N`2、複素数	`LDX1` ≥ `N`1 `LDY1` = `LDX1`	`LDX1` ≥ `N`1 `LDY1` ≥ `N`1
	`OPT` = 1 複素数-複素数逆方向 2 次元 FFT	`N`1 × `N`2、複素数	`N`1 × `N`2、複素数	`LDX1` ≥ `N`1 `LDY1` = `LDX1`	`LDX1` ≥ `N`1 `LDY1` = `LDX1`

注 - 表 13 に関して、次のことに注意してください。

LDX1 は入力配列のリーディングディメンジョンです。
LDY1 は出力配列のリーディングディメンジョンです。
N1 は FFT 問題の最初の次元です。
N2 は FFT 問題の 2 番目の次元です。
OPT = 0 でルーチンを呼び出して、ルーチンを初期化した場合に、実行される唯一のエラーチェックは、N1、N2 < 0 かどうかを判断することです。

使用例 12 2 次元配列の 2 次元実数-複素数 FFT および複素数-実数 FFT

次の例に、2 次元配列の 2 次元実数-複素数 FFT および複素数-実数 FFT を計算する方法を示します。

my_system% cat testsc2.f
       PROGRAM TESTSC2
       IMPLICIT NONE
       INTEGER, PARAMETER :: N1 = 3, N2 = 4, LDX1 = N1,
      $         LDY1 = N1/2+1, LDR1 = 2*(N1/2+1)
       INTEGER LW, IERR, I, J, K, IFAC(128*2)
       REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2)
       REAL :: V(LDR1,N2), X(LDX1, N2), Z(LDR1,N2),
      $        SW(2*N2), TRIGS(2*(N1+N2))
       COMPLEX :: Y(LDY1,N2)
       WRITE(*,*) $'Two-dimensional complex-to-real and real-to-complex FFT'
       WRITE(*,*)
       X = RESHAPE(SOURCE = (/.1, .2, .3, .4, .5, .6, .7, .8,
      $            2.0,1.0, 1.1, 1.2/), SHAPE=(/LDX1,N2/))
       DO I = 1, N2
          V(1:N1,I) = X(1:N1,I)
       END DO
       WRITE(*,*) 'X ='
       DO I = 1, N1
          WRITE(*,'(5(F5.1,2X))') (X(I,J), J = 1, N2)
       END DO
       WRITE(*,*)
* Initialize trig table and get factors of N1, N2
       CALL SFFTC2(0,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
      $            IFAC,SW,0,IERR)
* Compute 2-dimensional out-of-place forward FFT.
* Let FFT routine allocate memory.
* cannot do an in-place transform in X because LDX1 < 2*(N1/2+1)
       CALL SFFTC2(-1,N1,N2,ONE,X,LDX1,Y,LDY1,TRIGS,
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place forward FFT of X:'
       WRITE(*,*)'Y ='
       DO I = 1, N1/2+1
          WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J)),
      $           ',',AIMAG(Y(I,J)),')', J = 1, N2)
       END DO
       WRITE(*,*)
 
* Compute 2-dimensional in-place forward FFT. 
* Use workspace already allocated. 
* V which is real array containing input data is also 
* used to store complex results; as a complex array, its first 
* leading dimension is LDR1/2.
       CALL SFFTC2(-1,N1,N2,ONE,V,LDR1,V,LDR1/2,TRIGS,
      $            IFAC,SW,LW,IERR)
       WRITE(*,*) 'in-place forward FFT of X:'
       CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, 1, V, LDR1/2, N2)
* Compute 2-dimensional out-of-place inverse FFT. 
* Leading dimension of Z must be even
       CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Z,LDR1,TRIGS, 
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place inverse FFT of Y:'
       DO I = 1, N1
          WRITE(*,'(5(F5.1,2X))') (Z(I,J), J = 1, N2)
       END DO
       WRITE(*,*)
* Compute 2-dimensional in-place inverse FFT.
* Y which is complex array containing input data is also 
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
       CALL CFFTS2(1,N1,N2,SCALE,Y,LDY1,Y,2*LDY1,
      $            TRIGS,IFAC,SW,0,IERR)
       WRITE(*,*) 'in-place inverse FFT of Y:'
       CALL PRINT_COMPLEX_AS_REAL(N1, N2, 1, Y, 2*LDY1, N2)
       END PROGRAM TESTSC2
       SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K
       REAL A(LD1, LD2, *)
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
          END DO 
          WRITE(*,*)
       END DO
       END
 
       SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K 
       COMPLEX A(LD1, LD2, *)
       DO K = 1, N3 
          DO I = 1, N1 
             WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
      $              ',',AIMAG(A(I,J,K)),')', J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
       END
my_system% f95 -dalign testsc2.f -library=sunperf
my_system% a.out
Two-dimensional complex-to-real and real-to-complex FFT
x =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
out-of-place forward FFT of X:
Y =
(  8.9, 0.0) ( -2.9,  1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) (  0.5, -1.0) ( -0.5, 1.0) (  0.5, -1.0)
in-place forward FFT of X:
( 8.9, 0.0) ( -2.9, 1.8) ( -0.7, 0.0) ( -2.9, -1.8)
( -1.2, 1.3) ( 0.5, -1.0) ( -0.5, 1.0) ( 0.5, -1.0)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 2.0 1.2

3 次元 FFT ルーチン

Oracle Developer Studio パフォーマンスライブラリには、3 次元 FFT を計算するルーチンが含まれています。この場合、FFT は 3 次元配列の 3 つすべての次元に沿って計算されます。順方向 FFT は次を計算します:

$image:X(k,n,m) = {h = 0} から {N3 - 1} までと {l = 0} から {N2 - 1} までと {j = 0} から {N1 - 1} までの x(j,l,h) × e^{{-2πihm} / N3} × e^((-2πiln) / N2) × e^((-2πijk) / N1) の合計,{}改行{} k=0,...,N1 - 1 {}改行{} n=0,...,N2 - 1 {}改行{} m=0,...,N3 -1$ 、

また、逆方向 FFT は次を計算します:

$image:x(j,l,h) = {m = 0} から {N3 - 1} までと {n = 0} から {N2 - 1} までと {k = 0} から {N1 - 1} までの X(k,n,m) × e^((-2πihm) / N3) × e^((-2πiln) / N2) × e^((-2πijk) / N1) の合計,{}改行{} j = 0,...,N1 - 1 {}改行{} l=0, ...,N2 - 1 {}改行{} h = 0,...,N3 -1$

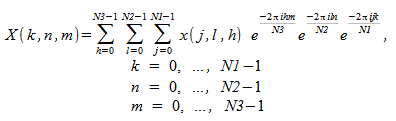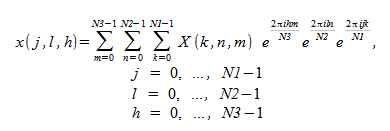
複素数-複素数変換で、入力の問題が N1 × N2 × N3 である場合、3 次元変換は、同様に N1 × N2 × N3 である複素数配列を生成します。実数-複素数 3 次元変換の計算時に、実数入力配列が次元 N1 × N2 × N3 である場合、結果は次の次元の複素数配列になります: 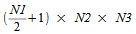image:((N1 / 2) + 1) × N2 × N3 。逆に、次元 N1 × N2 × N3 の複素数-実数 FFT の計算時、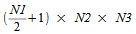複素数配列が入力として必要です。実数-複素数および複素数-実数の 1 次元 FFT と同様に、共役対称性のため、最初のみの 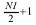image:(N1 / 2) + 1 複素数データポイントが最初の次元に沿って格納される必要があります。複素数部分配列 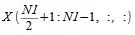image:X(N1 / 2) + 1: N1-1, :, :) は次から取得でき、 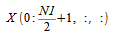image:X(0:(N1 / 2) + 1, :, :) 次のようになります。

image:X(k,n,m) = X * (N1 - k,n,m),{}改行{} k = {N1 / 2} + 1,...,N1 - 1 {}改行{} n = 0, ...,N2 - 1 {}改行{} m=0,...,N3 - 1

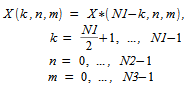
3 次元変換を計算するには、FFT ルーチンを 2 回呼び出す必要があります。1 回は初期化し、もう 1 回は実際に変換を計算します。初期化には、N1、N2、および N3 の係数と、それらの係数に関連付けられる三角法の重みの計算が含まれます。その後の順変換または逆変換では、N1、N2、および N3 が変更されないかぎり、初期化は必要ありません。

重要: 3 次元 FFT ルーチンからの戻り時に、Y(0 : N - 1, :, :) に変換結果が格納され、Y(N:LDY1-1, :, :) の元の内容が上書きされます。ここで、複素数-複素数および複素数-実数変換では N = N1 で、実数-複素数変換では N= 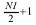image:(N1 / 2) + 1 (実数-複素数変換の場合) です。

表 14 に、単精度 3 次元 FFT ルーチンとその目的を示します。同じ情報は、データ型が倍精度と倍精度複素数であることを除いて、対応する倍精度ルーチンに適用します。マッピングについては、表 14 を参照してください。ルーチンとその引数の詳細な説明については、個々のマニュアルページを参照してください。

表 14 単精度 3 次元 FFT ルーチン

名前	目的	入力のサイズ、型	出力のサイズ、型	リーディングディメンジョン要件
`SFFTC3`	`OPT` = 0 初期化
	`OPT` = -1 実数-複素数順方向 3 次元 FFT	`N`1 × `N`2 × `N`3、実数	、複素数	`LDX1`=2 × `LDY1` `LDX2` ≥ `N`2 `LDY1` ≥ `LDY2` = `LDX2`	`LDX1` ≥ `N`1 `LDX2` ≥ `N`2 `LDY1` ≥ `LDY2` ≥ `N`2
`CFFTS3`	`OPT` = 0 初期化
	`OPT` = 1 複素数-実数逆方向 3 次元 FFT	、複素数	`N`1 × `N`2 × `N`3、実数	`LDX1` ≥ `LDX2` ≥ `N`2 `LDY1`=2 × `LDX1` `LDY2`=`LDX2`	`LDX1` ≥ `LDX2` ≥ `N`2 `LDY1` ≥ 2 × `LDX1` `LDY1` は偶数 `LDY2` ≥ `N`2
`CFFTC3`	`OPT` = 0 初期化
	`OPT` = -1 複素数-複素数順方向 3 次元 FFT	`N`1 × `N`2 × `N`3、複素数	`N`1 × `N`2 × `N`3、複素数	`LDX1` ≥ `N`1 `LDX2` ≥ `N`2 `LDY1`=`LDX1` `LDY2`=`LDX2`	`LDX1` ≥ `N`1 `LDX2` ≥ `N`2 `LDY1` ≥ `N`1 `LDY2` ≥ `N`2
	`OPT` = 1 複素数-複素数逆方向 3 次元 FFT	`N`1 × `N`2 × `N`3、複素数	`N`1 × `N`2 × `N`3、複素数	`LDX1` ≥ `N`1 `LDX2` ≥ `N`2 `LDY1`=`LDX1` `LDY2`=`LDX2`	`LDX1` ≥ `N`1 `LDX2` ≥ `N`2 `LDY1` ≥ `N`1 `LDY2` ≥ `N`2

注 - 表 14 に関して、次のことに注意してください。

LDX1 は入力配列の最初のリーディングディメンジョンです。
LDX2 は入力配列の 2 番目のリーディングディメンジョンです。
LDY1 は出力配列の最初のリーディングディメンジョンです。
LDY2 は出力配列の 2 番目のリーディングディメンジョンです。
N1 は FFT 問題の最初の次元です。
N2 は FFT 問題の 2 番目の次元です。
N3 は FFT 問題の 3 番目の次元です。
OPT = 0 でルーチンを呼び出して、ルーチンを初期化した場合に、実行される唯一のエラーチェックは、N1、N2、N3 < 0 かどうかを判断することです。

例 7-4 に、3 次元配列の 3 次元実数-複素数 FFT および複素数-実数 FFT を計算する方法を示します。

使用例 13 3 次元配列の 3 次元実数-複素数 FFT および複素数-実数 FFT

my_system% cat testsc3.f
       PROGRAM TESTSC3
       IMPLICIT NONE
       INTEGER LW, NCPUS, IERR, I, J, K, USING_THREADS, IFAC(128*3)
       INTEGER, PARAMETER :: N1 = 3, N2 = 4, N3 = 2, LDX1 = N1, 
      $                      LDX2 = N2, LDY1 = N1/2+1, LDY2 = N2,
      $                      LDR1 = 2*(N1/2+1), LDR2 = N2
       REAL, PARAMETER :: ONE = 1.0, SCALE = ONE/(N1*N2*N3)
 
       REAL :: V(LDR1,LDR2,N3), X(LDX1,LDX2,N3), Z(LDR1,LDR2,N3),
      $        TRIGS(2*(N1+N2+N3))
       REAL, DIMENSION(:), ALLOCATABLE :: SW
       COMPLEX :: Y(LDY1,LDY2,N3)
       WRITE(*,*)
      $'Three-dimensional complex-to-real and real-to-complex FFT'
       WRITE(*,*)
* get number of threads
       NCPUS = USING_THREADS()
* compute workspace size required
       LW = (MAX(MAX(N1,2*N2),2*N3) + 16*N3) * NCPUS
       ALLOCATE(SW(LW))
       X = RESHAPE(SOURCE = 
      $    (/ .1, .2, .3, .4, .5, .6, .7, .8, .9,1.0,1.1,1.2,
      $     4.1,1.2,2.3,3.4,6.5,1.6,2.7,4.8,7.9,1.0,3.1,2.2/),
      $     SHAPE=(/LDX1,LDX2,N3/))
       V = RESHAPE(SOURCE =
      $    (/.1,.2,.3,0.,.4,.5,.6,0.,.7,.8,.9,0.,1.0,1.1,1.2,0.,
      $     4.1,1.2,2.3,0.,3.4,6.5,1.6,0.,2.7,4.8,7.9,0.,
      $     1.0,3.1,2.2,0./), SHAPE=(/LDR1,LDR2,N3/))
       WRITE(*,*) 'X ='
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(F5.1,2X))') (X(I,J,K), J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
* Initialize trig table and get factors of N1, N2 and N3
       CALL SFFTC3(0,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
      $            IFAC,SW,0,IERR)
* Compute 3-dimensional out-of-place forward FFT. 
* Let FFT routine allocate memory.
* cannot do an in-place transform because LDX1 < 2*(N1/2+1)
       CALL SFFTC3(-1,N1,N2,N3,ONE,X,LDX1,LDX2,Y,LDY1,LDY2,TRIGS,
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place forward FFT of X:'
       WRITE(*,*)'Y ='
       DO K = 1, N3
          DO I = 1, N1/2+1
             WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))')('(',REAL(Y(I,J,K)),
      $              ',',AIMAG(Y(I,J,K)),')', J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
 
* Compute 3-dimensional in-place forward FFT. 
* Use workspace already allocated.
* V which is real array containing input data is also
* used to store complex results; as a complex array, its first
* leading dimension is LDR1/2.
       CALL SFFTC3(-1,N1,N2,N3,ONE,V,LDR1,LDR2,V,LDR1/2,LDR2,TRIGS,
      $            IFAC,SW,LW,IERR)
       WRITE(*,*) 'in-place forward FFT of X:'
       CALL PRINT_REAL_AS_COMPLEX(N1/2+1, N2, N3, V, LDR1/2, LDR2)
* Compute 3-dimensional out-of-place inverse FFT. 
* First leading dimension of Z (LDR1) must be even
       CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Z,LDR1,LDR2,TRIGS,
      $            IFAC,SW,0,IERR)
       WRITE(*,*) 'out-of-place inverse FFT of Y:'
       DO K = 1, N3
         DO I = 1, N1
            WRITE(*,'(5(F5.1,2X))') (Z(I,J,K), J = 1, N2)
         END DO
         WRITE(*,*)
       END DO
* Compute 3-dimensional in-place inverse FFT. 
* Y which is complex array containing input data is also
* used to store real results; as a real array, its first
* leading dimension is 2*LDY1.
       CALL CFFTS3(1,N1,N2,N3,SCALE,Y,LDY1,LDY2,Y,2*LDY1,LDY2,
      $            TRIGS,IFAC,SW,LW,IERR)
       WRITE(*,*) 'in-place inverse FFT of Y:'
       CALL PRINT_COMPLEX_AS_REAL(N1, N2, N3, Y, 2*LDY1, LDY2)
       DEALLOCATE(SW)
       END PROGRAM TESTSC3
       SUBROUTINE PRINT_COMPLEX_AS_REAL(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K
       REAL A(LD1, LD2, *)
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(F5.1,2X))') (A(I,J,K), J = 1, N2)
          END DO 
          WRITE(*,*)
       END DO
       END
       SUBROUTINE PRINT_REAL_AS_COMPLEX(N1, N2, N3, A, LD1, LD2)
       INTEGER N1, N2, N3, I, J, K
       COMPLEX A(LD1, LD2), *)
       DO K = 1, N3
          DO I = 1, N1
             WRITE(*,'(5(A1, F5.1,A1,F5.1,A1,2X))') ('(',REAL(A(I,J,K)),
      $              ',',AIMAG(A(I,J,K)),')', J = 1, N2)
          END DO
          WRITE(*,*)
       END DO
       END
my_system% f95 -dalign testsc3.f -xlibrary=sunperf
my_system% a.out
Three-dimensional complex-to-real and real-to-complex FFT
X =
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
out-of-place forward FFT of X:
Y =
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) (  6.0, 7.0) ( -7.0,  0.0) (  6.0, -7.0)
(  3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5,  0.7)
in-place forward FFT of X:
( 48.6, 0.0) ( -9.6, -3.4) ( 3.4, 0.0) ( -9.6, 3.4)
( -4.2, -1.0) ( 2.5, -2.7) ( 1.0, 8.7) ( 9.5, -0.7)
(-33.0, 0.0) (  6.0, 7.0) ( -7.0, 0.0) (  6.0, -7.0)
(  3.0, 1.7) ( -2.5, 2.7) ( -1.0, -8.7) ( -9.5, 0.7)
out-of-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2
in-place inverse FFT of Y:
0.1 0.4 0.7 1.0
0.2 0.5 0.8 1.1
0.3 0.6 0.9 1.2
4.1 3.4 2.7 1.0
1.2 6.5 4.8 3.1
2.3 1.6 7.9 2.2

インプレース実数-複素数または複素数-実数変換を実行する場合は、入力配列のサイズが、結果を保持するために十分に大きいことを注意して確認する必要があります。たとえば、入力の型が最初のリーディングディメンジョン N の複素数配列に格納されている複素数である場合、同じ配列を使用して、実数の結果を格納するには、実数出力配列としてのその最初のリーディングディメンジョンは 2 × N になります。逆に、入力の型が最初のリーディングディメンジョン 2 × N の実数配列に格納されている実数である場合、同じ配列を使用して、複素数の結果を格納するには、複素数出力配列としてのその最初のリーディングディメンジョンは N になります。インプレースおよびアウトオブプレース変換のリーディングディメンジョン要件については、表 12、表 13、および表 14 を参照してください。

1 次元および多次元 FFT で、実数-複素数変換または複素数-実数変換による実数データと複素数データ間の変換は、N1 実数データポイントが次に対応しているため混乱することがあります: 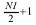image:(N1 / 2) + 1 複素数データポイント。N1 実数データポイントは N 1 複素数データポイントにマッピングしますが、複素数データには共役対称性があるため、 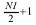image:(N1 / 2) + 1 データポイントは複素数-実数変換の入力として、および実数-複素数変換の出力としてのみ格納される必要があります。多次元 FFT では、対称性は最初だけでなく、すべての次元に沿って存在します。ただし、2 次元および 3 次元 FFT ルーチンは、2 番目と 3 番目の次元の複素数データをそっくりそのまま格納します。

FFT ルーチンは、任意のサイズの N1、N2、および N3 を受け入れますが、N1、N2、および N3 の値が相対的に小さい素数に分解できる場合に、FFT をもっとも効率的に計算できます。実数-複素数または複素数-実数変換は次の場合にもっとも効率的に計算できます:

image:N1, N2, N3 = 2^p × 3^q × 4^r × 5^s ,

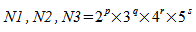また、複素数-複素数変換は次の場合にもっとも効率的に計算されます:

image:N1, N2, N3 = 2^p × 3^q × 4^r × 5^s × 7^t × 11^u × 13^v ,

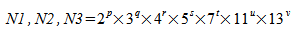ここで、p、q、r、s、t、u、および v は整数で、p、q、r、s、t、u、v ≥ 0 です。

使用例 14 に示すように、関数 xFFTOPT を使用して、最適なシーケンスの長さを判断できます。入力シーケンスの長さを考慮して、関数は元の長さにもっとも近いサイズの最適な長さを返します。

使用例 14 RFFTOPT の例

my_system% cat fft_ex01.f
      PROGRAM TEST
      INTEGER         N, N1, N2, N3, RFFTOPT
C
      N = 1024
      N1 = 1019
      N2 = 71 
      N3 = 49
C
      PRINT *, 'N Original  N Suggested'
      PRINT '(I5, I12)', (N, RFFTOPT(N)) 
      PRINT '(I5, I12', (N1, RFFTOPT(N1)) 
      PRINT '(I5, I12)', (N2, RFFTOPT(N2)) 
      PRINT '(I5, I12)', (N3, RFFTOPT(N3)) 
      END
 
my_system% f95 -dalign fft_ex01.f -library=sunperf
my_system% a.out
 N Original  N Suggested
 1024        1024
 1019        1024
   71          72
   49          49
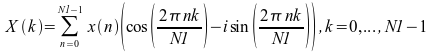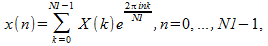
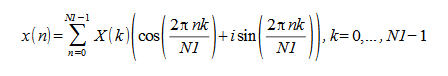
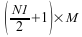