コサインおよびサイン変換

言語:

特殊な対称性を持つ DFT への入力はさまざまなアプリケーションで発生します。対称性を利用する変換は通常、実数-複素数および複素数-実数 FFT 変換などのように、ストレージと計算数を節約します。パフォーマンスライブラリコサインおよびサイン変換は、偶関数および奇関数内で検出された対称性プロパティーを利用する特殊なケースの FFT ルーチンです。

注 - Oracle Developer Studio パフォーマンスライブラリのサインおよびコサイン変換ルーチンは FFTPACK (http://www.netlib.org/fftpack/) に含まれるルーチンに基づいています。V 接頭辞が付いたルーチンは、VFFTPACK (http://www.netlib.org/vfftpack/) に含まれているルーチンに基づいたベクトル化したルーチンです。

高速コサインおよびサイン変換ルーチン

次の表に、Oracle Developer Studio パフォーマンスライブラリの高速コサインおよびサイン変換を示します。倍精度ルーチンの名前は角括弧で囲んでいます。名前が「V」で始まるルーチンは、1 つ以上のシーケンスの変換を同時に計算できます。名前が「I」で終わるものは、初期化ルーチンです。

表 15 偶数シーケンスの高速コサイン変換ルーチンとそれらの引数

ルーチン名	引数
`COST` `[DCOST]`	`(LEN+1`, `X,` `WORK)`
`COSTI` `[DCOSTI]`	`(LEN+1,` `WORK)`
`VCOST` `[VDCOST]`	`(M,` `LEN+1,` `X,` `WORK,` `LD,` `TABLE)`
`VCOSTI` `[VDCOSTI]`	`(LEN+1,` `TABLE)`

表 16 1/4 波偶数シーケンスの高速コサイン変換ルーチンとそれらの引数

ルーチン名	引数
`COSQF` `[DCOSQF]`	`(LEN,` `X,` `WORK)`
`COSQB` `[DCOSQB]`	`(LEN,` `X,` `WORK)`
`COSQI` `[DCOSQI]`	`(LEN,` `WORK)`
`VCOSQF` `[VDCOSQF]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VCOSQB` `[VDCOSQB]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VCOSQI` `[VDCOSQI]`	`(LEN,` `TABLE)`

表 17 奇数シーケンスの高速サイン変換ルーチンとそれらの引数

ルーチン名	引数
`SINT` `[DSINT]`	`(LEN-1,` `X,` `WORK)`
`SINTI` `[DSINTI]`	`(LEN-1,` `WORK)`
`VSINT` `[VDSINT]`	`(M,` `LEN-1,` `X,` `WORK,` `LD,` `TABLE)`
`VSINTI` `[VDSINTI]`	`(LEN-1,` `TABLE)`

表 18 1/4 波奇数シーケンスの高速サイン変換ルーチンとそれらの引数

ルーチン名	引数
`SINQF` `[DSINQF]`	`(LEN,` `X,` `WORK)`
`SINQB` `[DSINQB]`	`(LEN,` `X,` `WORK)`
`SINQI` `[DSINQI]`	`(LEN,` `WORK)`
`VSINQF` `[VDSINQF]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VSINQB` `[VDSINQB]`	`(M,` `LEN,` `X,` `WORK,` `LD,` `TABLE)`
`VSINQI` `[VDSINQI]`	`(LEN,` `TABLE)` 注記:

注 - 前の表に関して次の情報に注意してください。

M: 変換するシーケンスの数。
LEN、LEN-1、LEN+1: 入力シーケンスの長さ。
X: 変換するシーケンスを格納する実数の配列。出力で、実数変換結果は X に格納されます。
TABLE: 変換ルーチンに必要な変換サイズに固有の定数の配列。定数は初期化ルーチンによって計算されます。
WORK: 変換ルーチンに必要なワークスペース。単一のシーケンスを処理するルーチンで、WORK には初期化ルーチンによって計算された定数も格納されます。

高速サイン変換

よく見られる対称性のもう 1 つのタイプは、n = -N+1, …, 0, …, N の場合に x(n) = -x(-n) である奇数対称性です。高速コサイン変換の場合と同様に、高速サイン変換 (FST) は、奇数対称性を利用してメモリーと計算を節約します。実数奇数シーケンス x の場合、対称性は、x(0) = -x(0) = 0 であることを示します。したがって、x の長さが 2 N の場合、FST を計算するために、x の N = 1 の値のみ必要です。ルーチン SINT は単一の実数奇数シーケンスの FST を計算し、VSINT は 1 つ以上のシーケンスの FST を計算します。[V]SINT を呼び出す前に、入力長 N-1 に関連付けられた三角法の定数と係数を計算するために、[V]SINTI を呼び出す必要があります。FST はそれ自身の逆変換です。VSINT を 2 回呼び出すと、元の N -1 データポイントになります。SINT を 2 回呼び出すと、2N をかけた元の N -1 データポイントになります。

-N+1, …, 0, …, N の場合に x(n) = -x(-n - 1) のような対称性を持つ奇数シーケンスは、1/4 波奇数対称性があると言います。SINQF および SINQB はそれぞれ単一の実数 1/4 波奇数シーケンスの FST およびその逆変換を計算し、VSINQF および VSINQB は 1 つまたは複数のシーケンスを処理します。SINQB は正規化されないため、SINQB の入力として SINQF の結果を使用すると、4 N の係数でスケーリングされた元のシーケンスが生成されます。ただし、VSINQB は正規化されるため、VSINQF の呼び出しのあとの VSINQB の呼び出しによって、元のシーケンスが生成されます。1/4 波奇数対称性がある長さ 2 N の実数シーケンスの FST には、N 入力データポイントが必要で、N ポイントの結果シーケンスを生成します。[V]SINQI を呼び出して変換ルーチンを呼び出す前に初期化が必要です。

高速コサイン変換

実数偶数シーケンスを処理する FFT の特殊な形式は、高速コサイン変換 (FCT) です。実数シーケンス x は、x(n) = x(-n) の場合に偶数の対称性があると言われます。ここで n = -N + 1, …, 0, …, N です。長さ 2N のシーケンスの FCT には N + 1 入力データポイントが必要で、サイズ N + 1 のシーケンスを生成します。ルーチン COST は単一の実数偶数シーケンスの FCT を計算し、VCOST は 1 つ以上のシーケンスの FCT を計算します。[V]COST を呼び出す前に、[V]COSTI を呼び出して、入力長 N +1 に関連付けられる三角法の定数と係数を計算する必要があります。FCT はそれ自身の逆変換です。VCOST を 2 回呼び出すと、元の N +1 データポイントになります。COST を 2 回呼び出すと、2N をかけた元の N +1 データポイントになります。

n = ‐N + 1, … , 0, …, N の場合に、x(n) = x(-n - 1) のような対称性を持つ偶数シーケンス x は、1/4 波偶数対称性があると言います。COSQF および COSQB は単一の実数 1/4 波偶数シーケンスの FCT とその逆変換をそれぞれ計算します。VCOSQF および VCOSQB は 1 つ以上のシーケンスを処理します。[V]COSQB の結果は正規化されず、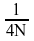 image:1 / 4N でスケーリングされた場合、元のシーケンスが取得されます。1/4 波実数対称性がある長さ 2N の実数シーケンスの FCT には、N の入力データポイントが必要で、N ポイントの結果シーケンスを生成します。変換ルーチンを呼び出す前に、[V]COSQI を呼び出して、初期化が必要です。

離散高速コサインおよびサイン変換とそれらの逆変換

Oracle Developer Studio パフォーマンスライブラリルーチンは、次のセクションの方程式を使用して、高速コサインおよびサイン変換と逆変換を計算します。

`[D]COST`: シーケンスの順方向および逆方向高速コサイン変換 (FCT)

シーケンスの順方向および逆方向 FCT は次のように計算されます。

image:X(k) = x(0) + 2 × {n=1} から {N-1} までの x(n) cos ((πnk) / N) の合計 + x(N) cos (πk), k=0,...,N

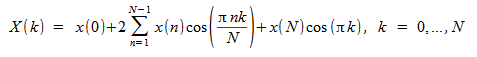
[D]COST 注記:

N ポイントシーケンスの FCT を計算するために、N + 1 の値が必要になります。
[D]COST は逆変換も計算します。[D]COST が 2 回呼び出されると、結果は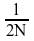でスケーリングされた元のシーケンスになります。

`V[D]COST`: 複数シーケンスの順方向および逆方向高速コサイン変換 (VFCT)

複数シーケンスの順方向および逆方向 FCT は次のように計算されます。

i = 0、M - 1 の場合

image:X(i,k) = ({x(i,0)} / 2N) + 1 / N × {n=1} から {N - 1} までの x(i,n) cos ({πnk} / N ) の合計 + (x(i,N) / 2N) cos (πk), k= 0, ..., N1 .

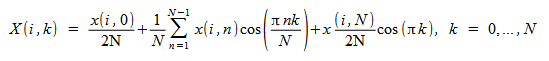V[D]COST 注記

M N ポイントシーケンスの VFCT を計算するために、M × (N+1) の値が必要になります。
入力および出力シーケンスは、行方向に格納されます。
V[D]COST は正規化され、それ自身の逆変換です。V[D]COST が 2 回呼び出されると、結果は元のデータになります。

`[D]COSQF`: 1/4 波偶数シーケンスの順方向 FCT

1/4 波偶数シーケンスの順方向 FCT は次のように計算されます。

image:X(k) = x(0)+ 2 × {n = 1} から {N - 1} までの x(n) cos ({π(2k+1)} / 2N) の合計, k= 0, ..., N - 1

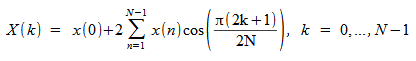
N ポイント 1/4 波偶数シーケンスの順方向 FCT を計算するために、N の値が必要です。

`[D]COSQB`: 1/4 波偶数シーケンスの逆方向 FCT

1/4 波偶数シーケンスの逆方向 FCT は次のように計算されます

image:x(n) = {k = 0} から {N - 1} までの X(k) cos ({πn (2k + 1)} / 2N), n = 0,...,N - 1 .

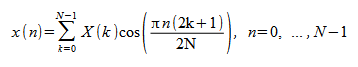順変換ルーチンと逆変換ルーチンを呼び出すと、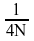 image:1 / 4N でスケーリングされた元の入力になります。

`V[D]COSQF`: 1 つ以上の 1/4 波偶数シーケンスの順方向 FCT

1 つまたは複数の 1/4 波偶数シーケンスの順方向 FCT は次のように計算されます

i = 0、M - 1 の場合

image:X(i,k) = 1 / N [ x(i,0) + 2 × {n = 1} から {N - 1} までの x(i,n) cos ({πn (2k + 1)} / 2N ) の合計], k = 0, ..., N - 1

V[D]COSQF 注記:

入力および出力シーケンスは、行方向に格納されます。
変換は正規化されるため、V[D]COSQF の呼び出し後すぐに、逆変換ルーチン V[D]COSQB が呼び出された場合、元のデータが取得されます。

`V[D]COSQB`: 1 つ以上の 1/4 波偶数シーケンスの逆方向 FCT

1 つ以上の 1/4 波偶数シーケンスの逆方向 FCT は次のように計算されます

i = 0、M - 1 の場合

image:x(i,n) = {k = 0} から {N - 1} までの X(i,k) cos ({πn (2k + 1)} / 2N) の合計, n = 0,...,N - 1

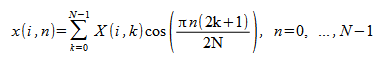
V[D]COSQB 注記:

入力および出力シーケンスは、行方向に格納されます。
変換は正規化されるため、V[D]COSQB が V[D]COSQF の呼び出し後すぐに呼び出された場合、元のデータが取得されます。

`[D]SINT`: シーケンスの順方向および逆方向高速サイン変換 (FST)

シーケンスの順方向および逆方向 FST は次のように計算されます

image:X(k) = 2 × {n = 0} から {N - 2} までの x(n) sin ({π(n+1)(k+1)} / N) の合計, k = 0,...,N - 2 .

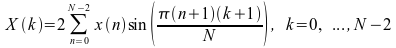[D]SINT 注記:

N ポイントシーケンスの FST を計算するために、N-1 の値が必要です。
[D]SINT は逆変換も計算します。[D]SINT が 2 回呼び出された場合、結果は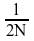でスケーリングされた元のシーケンスになります。

`V[D]SINT`: 複数シーケンスの順方向および逆方向高速サイン変換 (VFST)

複数シーケンスの順方向および逆方向高速サイン変換は次のように計算されます

i = 0、M - 1 の場合

image:X(i,k) = 2 / 2N の平方根 ×{n = 0} から {N - 2} までの x(i,n) sin ({π (n+1)(k+1)} / N) の合計, k = 0,...,N - 2 .

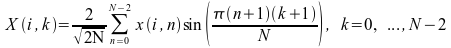V[D]SINT 注記:

M N ポイントシーケンスの VFST を計算するために、M × (N - 1) の値が必要です。
入力および出力シーケンスは、行方向に格納されます。
V[D]SINT は正規化され、それ自身の逆変換です。V[D]SINT を 2 回呼び出すと、元のデータが生成されます。

`[D]SINQF`: 1/4 波奇数シーケンスの順方向 FST

1/4 波奇数シーケンスの順方向 FST は次のように計算されます

image:X(k) = 2 × {n = 0} から {N - 2} までの x(n) sin ({π(n+1)(2k+1)} / 2N) の合計 + x(N - 1) cos (πk), k = 0,...,N - 1 .

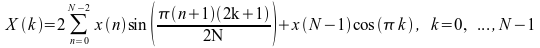N ポイント 1/4 波奇数シーケンスの順方向 FST を計算するために、N の値が必要になります。

`[D]SINQB`: 1/4 波奇数シーケンスの逆方向 FST

1/4 波奇数シーケンスの逆方向 FST は次のように計算されます

image:x(n) = 2 × {k = 0} から {N - 1} までの X(k) sin ({π(n+1)(2k + 1)} / 2N) の合計, n = 0,...,N - 1 .

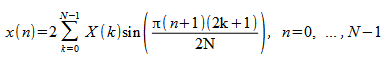順変換ルーチンと逆変換ルーチンを呼び出すと、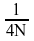 image:1 / 4N でスケーリングされた元の入力になります。

`V[D]SINQF`: 1 つ以上の 1/4 波奇数シーケンスの順方向 FST

1 つ以上の 1/4 波奇数シーケンスの順方向 FST は次のように計算されます

i = 0、M - 1 の場合

image:X(i,k) = 1 / 4N の平方根 × [ 2 × {n = 0} から {N - 2} までの x(n,i) sin ({π(n+1)(2k+1)} / 2N) の合計 + x (N - 1,i) cos πk ], k = 0, ...,N - 1 .

V[D]SINQF 注記:

入力および出力シーケンスは、行方向に格納されます。
変換は正規化されるため、V[D]SINQF の呼び出し後すぐに、逆変換ルーチン V[D]SINQB が呼び出された場合、元のデータが取得されます。

`V[D]SINQB`: 1 つ以上の 1/4 波奇数シーケンスの逆方向 FST

1 つ以上の 1/4 波奇数シーケンスの逆方向 FST は次のように計算されます

i = 0、M - 1 の場合

image:x(n,i) = 4 / 4N の平方根 × {k = 0} から {N - 1} までの X(k,i) sin({π (n+1)(2k+1)} / 2N ) の合計, n = 0, ...,N - 1 .

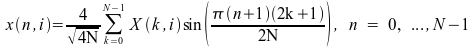V[D]SINQB 注記:

入力および出力シーケンスは、行方向に格納されます。
変換は正規化されるため、V[D]SINQB が V[D]SINQF の呼び出し後すぐに呼び出された場合、元のデータが取得されます。

高速コサイン変換の例

使用例 15 は、COST を呼び出して、実数偶数シーケンスの FCT と逆変換を計算します。実数シーケンスの長さが 2N の場合、N + 1 の入力データポイントのみを格納する必要があり、結果のデータポイントの数も N + 1 になります。結果は入力配列に格納されます。

使用例 15 単一の実数偶数シーケンスの FCT と逆方向 FCT の計算

my_system% cat cost.f
       program Drive cost
       implicit none
       integer,parameter :: len=4
       real x(0:len),work(3*(len+1)+15), z(0:len), scale
       integer i
       scale = 1.0/(2.0*len)
       call RANDOM_NUMBER(x(0:len))
       z(0:len) = x(0:len)
         write(*,'(a25,i1,a10,i1,a12)')'Input sequence of length ',
     $          len,' requires ', len+1,' data points'
       write(*,'(5(f8.3,2x),/)')(x(i),i=0,len)
       call costi(len+1, work)
       call cost(len+1, z, work)
       write(*,*)'Forward fast cosine transform'
       write(*,'(5(f8.3,2x),/)')(z(i),i=0,len)
       call cost(len+1, z, work)
       write(*,*)
     $    'Inverse fast cosine transform (results scaled by 1/2*N)'
       write(*,'(5(f8.3,2x),/)')(z(i)*scale,i=0,len)
       end
my_system% f95 -dalign cost.f -library=sunperf
my_system% a.out
Input sequence of length 4 requires 5 data points
0.557 0.603 0.210 0.352 0.867
Forward fast cosine transform
3.753 0.046 1.004 -0.666 -0.066
Inverse fast cosine transform (results scaled by 1/2*N)
0.557 0.603 0.210 0.352 0.867

使用例 16 では、VCOSQF および VCOSQB を呼び出して、2 つの実数 1/4 波偶数シーケンスの FCT と逆方向 FCT をそれぞれ計算しています。実数シーケンスの長さが 2N の場合、N の入力データポイントのみを格納する必要があり、結果のデータポイントの数も N になります。結果は入力配列に格納されます。

使用例 16 2 つの実数 1/4 波偶数シーケンスの FCT および逆方向 FCT の計算

my_system% cat vcosq.f
    program vcosq
    implicit none
    integer,parameter :: len=4, m = 2, ld = m+1
    real x(ld,len),xt(ld,len),work(3*len+15), z(ld,len)
    integer i, j
    call RANDOM_NUMBER(x)
    z = x
    write(*,'(a27,i1)')' Input sequences of length ',len
    do j = 1,m
       write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
 $     'seq',j,' = (',(x(j,i),i=1,len),')'
    end do
    call vcosqi(len, work)
    call vcosqf(m,len, z, xt, ld, work)
    write(*,*)
 $ 'Forward fast cosine transform for quarter-wave even sequences'
    do j = 1,m
       write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
 $     'seq',j,' = (',(z(j,i),i=1,len),')'
    end do
    call vcosqb(m,len, z, xt, ld, work)
    write(*,*)
 $  'Inverse fast cosine transform for quarter-wave even sequences'
  
    write(*,*)'(results are normalized)'
    do j = 1,m
       write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
 $     'seq',j,' = (',(z(j,i),i=1,len),')'
    end do
    end
 
my_system% f95 -dalign vcosq.f -library=sunperf
my_system% a.out
Input sequences of length 4
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
Forward fast cosine transform for quarter-wave even sequences
seq1 = (0.755 -.392 -.029 0.224 )
seq2 = (0.729 0.097 -.091 -.132 )
Inverse fast cosine transform for quarter-wave even sequences
(results are normalized)
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )

高速サイン変換の例

次の例の使用例 17 では、SINT を呼び出して、実数奇数シーケンスの FST と逆変換を計算しています。実数シーケンスの長さが 2N の場合、N - 1 の入力データポイントのみを格納する必要があり、結果のデータポイントの数も N- 1 になります。結果は入力配列に格納されます。

使用例 17 2 つの実数 1/4 波偶数シーケンスの FCT および逆方向 FCT の計算

my_system% cat sint.f
      program Drive sint
      implicit none
      integer,parameter :: len=4
      real x(0:len-2),work(3*(len-1)+15), z(0:len-2), scale
      integer i
      call RANDOM_NUMBER(x(0:len-2))
      z(0:len-2) = x(0:len-2)
      scale = 1.0/(2.0*len)  
      write(*,'(a25,i1,a10,i1,a12)')'Input sequence of length ',
    $       len,' requires ', len-1,' data points'   
      write(*,'(3(f8.3,2x),/)')(x(i),i=0,len-2)
      call sinti(len-1, work)
      call sint(len-1, z, work)
      write(*,*)'Forward fast sine transform'  
      write(*,'(3(f8.3,2x),/)')(z(i),i=0,len-2)
 
      call sint(len-1, z, work)
      write(*,*)
     $ 'Inverse fast sine transform (results scaled by 1/2*N)' 
      write(*,'(3(f8.3,2x),/)')(z(i)*scale,i=0,len-2)
      end
my_system% f95 -dalign sint.f -library=sunperf
my_system% a.out
Input sequence of length 4 requires 3 data points
0.557 0.603 0.210
Forward fast sine transform
2.291 0.694 -0.122
Inverse fast sine transform (results scaled by 1/2*N)
0.557 0.603 0.210

次の例の使用例 18 では、VSINQF および VSINQB を呼び出して、2 つの実数 1/4 波奇数シーケンスの FST と逆方向 FST をそれぞれ計算しています。実数シーケンスの長さが 2N の場合、N の入力データポイントのみを格納する必要があり、結果のデータポイントの数も N になります。結果は入力配列に格納されます。

使用例 18 2 つの実数 1/4 波奇数シーケンスの FST および逆方向 FST の計算

my_system% cat vsinq.f
      program vsinq
      implicit none
      integer,parameter :: len=4, m = 2, ld = m+1
      real x(ld,len),xt(ld,len),work(3*len+15), z(ld,len)
      integer i, j
      call RANDOM_NUMBER(x)
      z = x
      write(*,'(a27,i1)')' Input sequences of length ',len
      do j = 1,m
         write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
     $         'seq',j,' = (',(x(j,i),i=1,len),')'
      end do
      call vsinqi(len, work)
      call vsinqf(m,len, z, xt, ld, work)
      write(*,*)
    $ 'Forward fast sine transform for quarter-wave odd sequences'
      do j = 1,m
      write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
    $       'seq',j,' = (',(z(j,i),i=1,len),')'
      end do
 
      call vsinqb(m,len, z, xt, ld, work)
      write(*,*)
    $ 'Inverse fast sine transform for quarter-wave odd sequences'
      write(*,*)'(results are normalized)'
      do j = 1,m
      write(*,'(a3,i1,a4,4(f5.3,2x),a1,/)')
    $       'seq',j,' = (',(z(j,i),i=1,len),')'
      end do 
      end
my_system% f95 vsinq.f -library=sunperf
my_system% a.out
Input sequences of length 4
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )
Forward fast sine transform for quarter-wave odd sequences
seq1 = (0.823 0.057 0.078 0.305 )
seq2 = (0.654 0.466 -.069 -.037 )
Inverse fast sine transform for quarter-wave odd sequences
(results are normalized)
seq1 = (0.557 0.352 0.990 0.539 )
seq2 = (0.603 0.867 0.417 0.156 )