畳み込みおよび相関

言語:

信号処理分野で特に頻繁に見られる FFT の 2 つの用途は、離散畳み込み演算と離散相関演算です。

畳み込み演算

2 つの関数 x(t) と y(t) がある場合、 x(t) および y(t) の畳み込みのフーリエ変換は、x * y で示され、個々のフーリエ変換の積になります。DFT (x * y)=X (·) Y (* は畳み込み演算を示し、(·) は点別乗算を示します)。

一般に、x(t) は通常、等間隔での x(t) の一周期の有限期間でサンプリングされた一連の N データポイント x_j, j = 0, …, N -1 によって離散的に表される連続した定期的な信号です。y(t) は通常、ゼロから始まり、最大値に達したあとにゼロに戻る応答です。等間隔での y(t) の離散化は、一連の N データポイント、y_k, k = 0, …, N -1 を生成します。y_k の実際のサンプリングの数が N 未満である場合、データはゼロでパディングできます。離散畳み込みは次のように定義できます

$image:(x * y)_j ≡ {k= {-N / 2} + 1} から {N / 2} までの x_{j-k} y_k の合計, j = 0, ..., N-1$

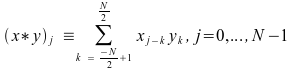
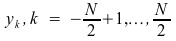image:y_k,k = -(N / 2) + 1, ..., N / 2 の値

は k = 0, …, N -1 の値と同じですが、循環した順序です。

Oracle Developer Studio パフォーマンスライブラリルーチンにより、k = 0, …, N -1 で上記の定義を使用するか、または FFT を使用して、畳み込みを計算できます。FFT を使用して、2 つのシーケンスの畳み込みを計算する場合、次の手順を実行します。

X = x の順方向 FFT を計算します
Y = y の順方向 FFT を計算します
Z = X (·) Y <=> DFT (x * y) を計算します
z = Z; z = (x * y) の逆方向 FFT を計算します

畳み込みの興味深い特性の 1 つは、2 つの多項式の積が実際の畳み込みであることです。m 項の多項式

a(x) = a₀ + a₁x + ... + a_m-1x^m-1

と n 項の多項式

b(x) = b₀ + b₁x + ... + b_n-1x^n-1

の積には、次によって取得可能な m+n-1 係数があります。

$image:c_k = {j = max ((k-(m-1)),0)} から {min (k,n-1)} までの a_j b_{k-j} の合計$

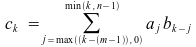
ここで k = 0, …, m + n - 2 です。

相関演算

畳み込みに密接に関係があるのが、相関演算です。これは、直接に重複しているか、一方が他方と相対的にシフトされている場合に、2 つのシーケンスの相関を計算します。畳み込みと同様に、FFT を使用して、次のように 2 つのシーケンスの相関を効率的に計算できます。

2 つの入力シーケンスの FFT を計算します。
一方のシーケンスの結果の変換と他方の変換のシーケンスの複素共役の点別の積を計算します。
積の逆方向 FFT を計算します。

パフォーマンスライブラリ内のルーチンにより、次の定義で相関を計算することもできます。

$image:Corr (x,y)_j ≡ {k=0} から {N-1} までの x_{j+k} y_k の合計, j = 0,..., N-1$

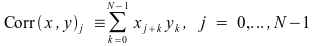
畳み込み演算と相関演算のサンプリング入力データを解釈する方法は、数多くあります。畳み込みルーチンと相関ルーチンの引数リストには、次のケースを処理するためのパラメータが含まれます。

信号関数や応答関数は、さまざまなサンプリング時間に開始できます。
信号の一部のみを出力に含めることもできます。
信号関数や応答関数は、明示的に格納されていない 1 つ以上のゼロから開始できます。

Oracle Developer Studio パフォーマンスライブラリの畳み込みルーチンと相関ルーチン

Oracle Developer Studio パフォーマンスライブラリには、表 19 に示す畳み込みルーチンが含まれています。

表 19 畳み込みおよび相関ルーチン

ルーチン	引数	機能
`SCNVCOR`、 `DCNVCOR`、 `CCNVCOR`、 `ZCNVCOR`	`CNVCOR,FOUR,NX,X,IFX, INCX,NY,NPRE,M,Y,IFY, INC1Y,INC2Y,NZ,K,Z, IFZ,INC1Z,INC2Z,WORK, LWORK`	1 つ以上のベクトルによるフィルタの畳み込みまたは相関
`SCNVCOR2`、 `DCNVCOR2`、 `CCNVCOR2`、 `ZCNVCOR2`	`CNVCOR,METHOD,TRANSX, SCRATCHX,TRANSY, SCRATCHY,MX,NX,X,LDX, MY,NY,MPRE,NPRE,Y,LDY, MZ,NZ,Z,LDZ,WORKIN, LWORK`	2 つの行列の 2 次元畳み込みまたは相関
`SWIENER`、`DWIENER`	`N_POINTS,ACOR,XCOR, FLTR,EROP,ISW,IERR`	2 つの信号のウィーナーデコンボリューション

[S,D,C,Z]CNVCOR ルーチンは、1 つ以上の入力ベクトルでフィルタの畳み込みや相関を計算するために使用されます。[S,D,C,Z]CNVCOR2 ルーチンは、2 つの行列の 2 次元畳み込みまたは相関を計算するために使用します。

畳み込みルーチンと相関ルーチンの引数

1 次元の畳み込みルーチンと相関ルーチンでは、表 20 に示す引数を使用します。

表 20 1 次元畳み込みおよび相関ルーチン SCNVCOR、DCNVCOR、CCNVCOR、および ZCNVCOR の引数

引数	定義
`CNVCOR`	`'V'` または `'v'` は、畳み込みを計算することを指定します。`'R'` または `'r'` は相関を計算することを指定します。
`FOUR`	`'T'` または `'t'` はフーリエ変換法を使用することを指定します。`'D'` または `'d'` は、畳み込みや相関を畳み込みと相関の定義から計算する直接法を使用することを指定します。畳み込む 2 つのシーケンスの長さが似ている場合、FFT 法は直接法より高速です。ただし、小さいフィルタで大きな時系列信号を畳み込む場合など、一方のシーケンスが他方よりはるかに大きい場合、FFT ベースの方法よりも直接法のほうが実行が速くなります。
`NX`	フィルタベクトルの長さで、`NX` ≥ 0 です。
`X`	フィルタベクトル
`IFX`	`X` の最初の要素のインデックスで、`NX` ≥ `IFX` ≥ 1
`INCX`	`X` のベクトルの要素間の刻み幅で、`INCX` > 0 です。
`NY`	入力ベクトルの長さで、`NY` ≥ 0 です。
`NPRE`	`Y` ベクトルの前に付ける暗黙的なゼロの数で、`NPRE` ≥ 0 です。
`M`	入力ベクトルの数で、`M` ≥ 0 です。
`Y`	入力ベクトル。
`IFY`	`Y` の最初の要素のインデックスで、`NY` ≥ `IFY` ≥ 1
`INC1Y`	`Y` の入力ベクトルの要素間の刻み幅で、`INC1Y` > 0 です。
`INC2Y`	`Y` の入力ベクトル間の刻み幅で、`INC2Y` > 0 です。
`NZ`	出力ベクトルの長さで、`NZ` ≥ 0 です。
`K`	`Z` ベクトルの数で、`K` ≥ 0 です。`K` < `M` である場合、最初の `K` ベクトルのみが処理されます。`K` > `M` である場合、すべての入力ベクトルが処理され、終了時に、最後の `M`-`K` 出力ベクトルにゼロが設定されます。
`Z`	結果ベクトル
`IFZ`	`Z` の最初の要素のインデックスで、`NZ` ≥ `IFZ` ≥ 1
`INC1Z`	`Z` の出力ベクトルの要素間の刻み幅で、`INCYZ` > 0 です。
`INC2Z`	`Z` の出力ベクトル間の刻み幅で、`INC2Z` > 0 です。
`WORK`	作業配列
`LWORK`	作業配列の長さ

2 次元の畳み込みルーチンと相関ルーチンは、表 21 に示す引数を使用します。

表 21 2 次元畳み込みおよび相関ルーチン SCNVCOR2、DCNVCOR2、CCNVCOR2、および ZCNVCOR2 の引数

引数	定義
`CNVCOR`	`'V'` または `'v'` は、畳み込みを計算することを指定します。`'R'` または `'r'` は相関を計算することを指定します。
`METHOD`	`'T'` または `'t'` はフーリエ変換法を使用することを指定します。`'D'` または `'d'` は、畳み込みや相関を畳み込みと相関の定義から計算する直接法を使用することを指定します。畳み込む 2 つの行列のサイズが似ている場合、FFT 法は直接法より高速です。ただし、小さいフィルタで大きなデータセットを畳み込む場合など、一方のシーケンスが他方よりはるかに大きい場合、FFT ベースの方法よりも直接法のほうが実行が速くなります。
`TRANSX`	`'N'` または `'n'` は、`X` が最初の行列であることを指定し、`'T'` または `'t'` は、`X` の転置行列がフィルタ行列であることを指定します
`SCRATCHX`	`'N'` または `'n'` は、`X` を保持する必要があることを指定し、`'S'` または `'s'` は `X` をスクラッチスペースに使用できることを指定します。`X` がスクラッチスペースに使用された呼び出しから戻ったあと、`X` の内容は未定義になります。
`TRANSY`	`'N'` または `'n'` は `Y` が入力行列であることを指定し、`'T'` または `'t'` は `Y` の転置行列が入力行列であることを指定します
`SCRATCHY`	`'N'` または `'n'` は、`Y` を保持する必要があることを指定し、`'S'` または `'s'` は `Y` をスクラッチスペースに使用できることを指定します。`Y` がスクラッチスペースに使用された呼び出しから戻ったあと、`X` の内容は未定義になります。
`MX`	フィルタ行列 `X` の行数で、`MX` ≥ 0
`NX`	フィルタ行列 `X` の列数で、`NX` ≥ 0
`X`	フィルタ行列。`X` は `SCRATCHX` が `'N'` または `'n'` の場合に終了時に変更されず、`SCRATCHX` が `'S'` または `'s'` の場合は終了時に未定義になります。
`LDX`	フィルタ行列 `X` を格納する配列のリーディングディメンジョン。
`MY`	入力行列 `Y` の行数で、`MY` ≥ 0 です。
`NY`	入力行列 `Y` の列数で、`NY` ≥ 0 です。
`MPRE`	入力行列 `Y` ベクトルの各行の前に付ける暗黙的なゼロの数で、`MPRE` ≥ 0 です。
`NPRE`	入力行列 `Y` の各列の前に付ける暗黙的なゼロの数で、`NPRE` ≥ 0 です。
`Y`	入力行列。`Y` は `SCRATCHY` が `'N'` または `'n'` の場合に終了時に変更されず、`SCRATCHY` が `'S'` または `'s'` の場合は終了時に未定義になります。
`LDY`	入力行列 `Y` を格納する配列のリーディングディメンジョン。
`MZ`	出力ベクトルの数で、`MZ` ≥ 0 です。
`NZ`	出力ベクトルの長さで、`NZ` ≥ 0 です。
`Z`	結果ベクトル
`LDZ`	結果の行列 `Z` を格納する配列のリーディングディメンジョンで、`LDZ` ≥ `MAX(1,MZ)` です。
`WORKIN`	作業配列
`LWORK`	作業配列の長さ

畳み込みルーチンと相関ルーチンの作業配列 `WORK`

1 次元および 2 次元畳み込みルーチンと相関ルーチンで使用される WORK 作業配列の最小次元は、表 24 に示しています。1 次元畳み込みルーチンと相関ルーチンの最小次元は、引数 NPRE、NX、NY、および NZ の値によって異なります。

2 次元畳み込みルーチンと相関ルーチンの最小次元は、表 22 に示す引数の値によって異なります。

表 22 2 次元ルーチンの最小作業配列サイズに影響する引数: SCNVCOR2、DCNVCOR2、CCNVCOR2、ZCNVCOR2

引数	定義
`MX`	フィルタ行列の行数
`MY`	入力行列の行数
`MZ`	出力ベクトル数
`NX`	フィルタ行列の列数
`NY`	入力行列の列数
`NZ`	出力ベクトルの長さ
`MPRE`	入力行列の各行の前に付ける暗黙的なゼロの数
`NPRE`	入力行列の各列の前に付ける暗黙的なゼロの数
`MPOST`	`MAX(0,MZ-MYC)`
`NPOST`	`MAX(0,NZ-NYC)`
`MYC`	`MPRE` + `MPOST` + `MYC_INIT`、ここで `MYC_INIT` は、表 23 に示すように、フィルタ行列と入力行列によって異なります。
`NYC`	`NPRE` + `NPOST` + `NYC_INIT`、ここで `NYC_INIT` は、表 23 に示すように、フィルタ行列と入力行列によって異なります。

MYC_INIT および NYC_INIT は次によって異なります。ここで、X はフィルタ行列で、Y は入力行列です。

表 23 MYC_INIT および NYC_INIT の依存関係

ルーチン	Y		Transpose(Y)
	X	Transpose(X)	X	Transpose(X)
`MYC_INIT`	`MAX(MX,MY)`	`MAX(NX,MY)`	`MAX(MX,NY)`	`MAX(NX,NY)`
`NYC_INIT`	`MAX(NX,NY)`	`MAX(MX,NY)`	`MAX(NX,MY)`	`MAX(MX,MY)`

最小の作業配列サイズに割り当てられる値を、表 24 に示します。

表 24 畳み込みルーチンと相関ルーチンで使用される WORK 作業配列の最小次元とデータ型

ルーチン	最小作業配列サイズ (`WORK`)	型
`SCNVCOR、DCNVCOR`	`4*(MAX(NX,NPRE+NY)` `+ MAX(0,NZ-NY))`	`REAL、REAL*8`
`CCNVCOR`、`ZCNVCOR`	`2*(MAX(NX,NPRE+NY)` `+ MAX(0,NZ‐NY)))`	`COMPLEX、COMPLEX*16`
`SCNVCOR2`^†、`DCNVCOR2`^†	`MY` `+` `NY` `+` `30`	`COMPLEX、COMPLEX*16`
`CCNVCOR2`^†、`ZCNVCOR2`^†	`MY` = `NY` の場合: `MYC + 8`、`MY` ≥ `NY の場合: MYC + NYC + 16`	`COMPLEX、COMPLEX*16`

LWORK によって示されるワークスペースのサイズが十分に大きくない場合、ルーチン内でメモリーが割り当てられます。

サンプルプログラム: 畳み込み

次の例は、CCNVCOR を使用して 2 つの複素数ベクトルの FFT 畳み込みを実行します。

使用例 19 フーリエ変換法と複素数データを使用した 1 次元畳み込み

my_system% cat con_ex20.f
      PROGRAM TEST
C
      INTEGER           LWORK
      INTEGER           N
      PARAMETER        (N = 3)
      PARAMETER        (LWORK = 4 * N + 15)
      COMPLEX           P1(N), P2(N), P3(2*N-1), WORK(LWORK)
      DATA P1 / 1, 2, 3 /,  P2 / 4, 5, 6 /
C
      EXTERNAL          CCNVCOR
C
      PRINT *, 'P1:'
      PRINT 1000, P1
      PRINT *, 'P2:'
      PRINT 1000, P2
 
      CALL CCNVCOR ('V', 'T', N, P1, 1, 1, N, 0, 1, P2, 1, 1, 1,
     $              2 * N - 1, 1, P3, 1, 1, 1, WORK, LWORK)
C
      PRINT *, 'P3:'
      PRINT 1000, P3
C
 1000 FORMAT (1X, 100(F4.1,' +',F4.1,'i  '))
C
      END
my_system% f95 -dalign con_ex20.f -xlibrary=sunperf
my_system% a.out
 P1:
  1.0 + 0.0i   2.0 + 0.0i   3.0 + 0.0i  
 P2:
  4.0 + 0.0i   5.0 + 0.0i   6.0 + 0.0i  
 P3:
  4.0 + 0.0i  13.0 + 0.0i  28.0 + 0.0i  27.0 + 0.0i  18.0 + 0.0i

引数の別名化またはさまざまな INC 引数の不適切に選択した値のため、いずれかのベクトルが書き込み可能なベクトルに重複している場合、結果は未定義になり、実行のたびにさまざまに異なることがあります。

もっとも一般的な計算の形式で、もっとも高速に実行するケースは、フィルタベクトル X を Y の列に格納されている一連のベクトルに適用し、結果を Z の列に配置することです。この場合、INCX = 1、INC1Y = 1、INC2Y ≥ NY、INC1Z = 1、INC2Z ≥ NZ です。別の一般的な形式は、フィルタベクトル X を Y の行に格納されている一連のベクトルに適用し、結果を Z の行に格納することです。この場合、INCX = 1、INC1Y ≥ NY、INC2Y = 1、INC1Z ≥ NZ、INC2Z = 1 です。

畳み込みを使用して、多項式の積を計算できます。次の例の使用例 20 は SCNVCOR を使用して、1 + 2x + 3x² と 4 + 5x + 6x² の積を計算しています。

使用例 20 フーリエ変換法と実数データを使用した 1 次元畳み込み

my_system% cat con_ex21.f
      PROGRAM TEST
      INTEGER     LWORK, NX, NY, NZ
      PARAMETER  (NX = 3)
      PARAMETER  (NY = NX)
      PARAMETER  (NZ = 2*NY-1)
      PARAMETER  (LWORK = 4*NZ+32)
      REAL        X(NX), Y(NY), Z(NZ), WORK(LWORK)
C
      DATA X / 1, 2, 3 /,  Y / 4, 5, 6 /, WORK / LWORK*0 /
C
      PRINT 1000, 'X'
      PRINT 1010, X
      PRINT 1000, 'Y'
      PRINT 1010, Y
      CALL SCNVCOR ('V', 'T', NX, X, 1, 1,   
     $NY, 0, 1, Y, 1, 1, 1,   NZ, 1, Z, 1, 1, 1, WORK, LWORK)
      PRINT 1020, 'Z'
      PRINT 1010, Z
 1000 FORMAT (1X, 'Input vector ', A1)
 1010 FORMAT (1X, 300F5.0)
 1020 FORMAT (1X, 'Output vector ', A1)
      END
my_system% f95 -dalign con_ex21.f -library=sunperf
my_system% a.out
 Input vector X
    1.   2.   3.
 Input vector Y
    4.   5.   6.
 Output vector Z
    4.  13.  28.  27.  18.

上の例のように、出力ベクトルを入力ベクトルより大きくすると、入力の末尾に暗黙的にゼロが追加されます。すべてのベクトルで実際にゼロは必要なく、例ではまったく使用されていませんが、暗黙的なゼロで行われるパディングは、入力ベクトルの循環桁送りではなく、切り捨て桁送りの効果があります。

次の例の使用例 21 では、ベクトル [1、2、3] と初期列ベクトル [4、5、6] で定義された巡回行列間の積を計算しています。

使用例 21 ベクトルと巡回行列の積を計算するために使用される畳み込み

my_system% cat con_ex22.f 
      PROGRAM TEST
C
      INTEGER     LWORK, NX, NY, NZ
      PARAMETER  (NX = 3)
      PARAMETER  (NY = NX)
      PARAMETER  (NZ = NY)
      PARAMETER  (LWORK = 4*NZ+32)
      REAL        X(NX), Y(NY), Z(NZ), WORK(LWORK)
C
      DATA X / 1, 2, 3 /,  Y / 4, 5, 6 /, WORK / LWORK*0 /
C
      PRINT 1000, 'X'
      PRINT 1010, X
      PRINT 1000, 'Y'
      PRINT 1010, Y
      CALL SCNVCOR ('V', 'T', NX, X, 1, 1,   
     $NY, 0, 1, Y, 1, 1, 1,   NZ, 1, Z, 1, 1, 1, 
     $WORK, LWORK)
      PRINT 1020, 'Z'
      PRINT 1010, Z
C
 1000 FORMAT (1X, 'Input vector ', A1)
 1010 FORMAT (1X, 300F5.0)
 1020 FORMAT (1X, 'Output vector ', A1)
      END
my_system% f95 -dalign con_ex22.f -library=sunperf
my_system% a.out
 Input vector X
    1.   2.   3.
 Input vector Y
    4.   5.   6.
 Output vector Z
   31.  31.  28.

次の例と前の例の違いは、出力ベクトルの長さが入力ベクトルの長さと同じであるため、入力ベクトルの末尾に暗黙的なゼロがありません。桁送りする暗黙的なゼロがないと、前の例の切り捨て桁送りの効果は発生せず、循環桁送りは巡回行列の積になります。

使用例 22 直接法を使用した 2 次元折り畳み

my_system% cat con_ex23.f
      PROGRAM TEST
C
      INTEGER           M, N
      PARAMETER        (M = 2)
      PARAMETER        (N = 3)
C
      INTEGER           I, J
      COMPLEX           P1(M,N), P2(M,N), P3(M,N)
      DATA P1 / 1, -2, 3, -4, 5, -6 /,  P2 / -1, 2, -3, 4, -5, 6 /
      EXTERNAL          CCNVCOR2
C
      PRINT *, 'P1:'
      PRINT 1000, ((P1(I,J), J = 1, N), I = 1, M)
      PRINT *, 'P2:'
      PRINT 1000, ((P2(I,J), J = 1, N), I = 1, M)
C
      CALL CCNVCOR2 ('V', 'Direct', 'No Transpose X', 'No Overwrite X',
     $   'No Transpose Y', 'No Overwrite Y', M, N, P1, M,
     $   M, N, 0, 0, P2, M, M, N, P3, M, 0, 0)
C
      PRINT *, 'P3:'
      PRINT 1000, ((P3(I,J), J = 1, N), I = 1, M)
C
 1000 FORMAT (3(F5.1,' +',F5.1,'i  '))
C
      END
my_system% f95 -dalign con_ex23.f -library=sunperf
my_system% a.out
 P1:
  1.0 +  0.0i    3.0 +  0.0i    5.0 +  0.0i  
 -2.0 +  0.0i   -4.0 +  0.0i   -6.0 +  0.0i  
 P2:
 -1.0 +  0.0i   -3.0 +  0.0i   -5.0 +  0.0i  
  2.0 +  0.0i    4.0 +  0.0i    6.0 +  0.0i  
 P3:
-83.0 +  0.0i  -83.0 +  0.0i  -59.0 +  0.0i  
 80.0 +  0.0i   80.0 +  0.0i   56.0 +  0.0i